Cours en ligne Physique-Chimie en Maths Spé

Chapitres Physique-Chimie en MP, PSI, PC, MPI, TSI, PT

Cours sur ondes électromagnétiques dans les milieux en MPI, MP, PSI, PC et PT

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercics et corrigés

Accorder du temps à la révision du cours des ondes électromagnétiques en physique chimie est d’une importance capitale pour les étudiants en maths spé, car cette matière occupe une place primordiale dans leur programme. Nous aborderons des concepts de thermodynamique en physique-chimie, notamment Pseudo-OPPH, Vitesse de groupe, vitesse de phase en prépa, Plasma et OEM dans les conducteurs ohmiques. Se tourner vers des cours particuliers en physique chimie peut également être bénéfique pour pallier d’éventuels blocages au cours de l’année. Il est incontestable que posséder une solide maîtrise de la physique chimie constitue un élément essentiel pour réussir les concours en MP, PC, PSI, MPI.

Pseudo-OPPH en maths spé

Méthode 1 : pseudo-OPPH.

Une pseudo-OPPH est une Onde (les champs dépendent de l’espace et du temps) Plane (dans un plan donné, les champs sont uniformes) Progressive (le champ varie selon $\omega t-\vec{k}\cdot\vec{OM}$ ) Harmonique (fonction trigonométrique monochromatique de pulsation $\omega$ ) dans laquelle le vecteur d’onde s’écrit $\underline{k}\vec{u}$ où $\underline{k}$ est complexe et $\vec{u}$ est un vecteur unitaire dans le sens et la direction de propagation.

En formalisme complexe, si $\underline{V}$ est un champ scalaire et $\vec{\underline{A}}$ un champ vectoriel

$\frac{\partial\vec{\underline{A}}}{\partial t}=i\omega\vec{\underline{A}}$ et $\frac{\partial\underline{V}}{\partial t}=i\omega\underline{V}$

$\mathrm{div}\vec{\underline{A}}=-i\vec{\underline{k}}\cdot\vec{\underline{A}}$ et $\vec{\mathrm{grad}}\underline{V}=-i\vec{\underline{k}}\cdot \underline{V}$

$\vec{\mathrm{rot}}\vec{\underline{A}}=-i\vec{\underline{k}}\wedge\vec{\underline{A}}$

Exemple.

Dans le vide, traduire les quatre équations de Maxwell en formalisme complexe.

Méthode 2. Équation de dispersion

En combinant les diverses relations, on obtient une équation indépendante des champs, en $\underline{k}$ , en général du second degré, dans laquelle interviennent les différents paramètres du problème et la variable $\omega$ : c’est l’équation de dispersion.

Remarque : dans le maniement des relations, on est souvent amené à utiliser la formule du double produit vectoriel :

$\vec{u}\wedge(\vec{v}\wedge\vec{w})=(\vec{u}\cdot\vec{w})\vec{v}-(\vec{u}\cdot\vec{w})\vec{v}$

Sa résolution donne en général deux solutions complexes qui correspondent aux deux sens de propagation possibles pour l’onde. On note

$\underline{k}=k'+ik''$

Exemple.

Établir l’équation de dispersion pour les ondes électromagnétiques dans le vide.

Méthode 3. Type d’onde selon les signes de $k'$ et $k''$ .

Posons $\vec{\underline{k}}=\underline{k}\vec{u}_x$

En injectant dans l’expression de la pseudo-OPPH, on a

$\displaystyle{\vec{\underline{A}}=\vec{\underline{A}}_0e^{k''x}e^{i(\omega t-k'x)}}$

soit en posant $\displaystyle{\vec{\underline{A}}_0=\vec{A}_0e^{i\varphi}}$

$\displaystyle{\vec{\underline{A}}=\vec{A}_0e^{k''x}e^{i(\omega t-k'x+\varphi)}}$

et en grandeurs réelles

$\displaystyle{\vec{A}=\vec{A}_0e^{k''x}\cos(\omega t-k'x+\varphi)}$

On en déduit

* Si $k''=0$ , onde plane progressive harmonique non atténuée, non amplifiée.

* Si $k'=0$ , onde stationnaire, sans propagation, évanescente si $k''<0$ et $x$ défini sur $[a,+\infty[$

Si $k'k''<0$ (cas le plus fréquent), onde progressive atténuée.

Si $k'k''>0$ (cas rare mais pas impossible dans des conditions particulières, par exemple où le milieu donne de l’énergie à l’onde), onde progressive amplifiée.

Exemple

L’équation de dispersion s’écrit

$\underline{k}^2=k_0^2\left[1-i\varepsilon\right]$ avec $k_0>0$ et $\varepsilon\ll 1$ .

Donner la valeur approchée de $\underline{k}$ et préciser le type d’onde.

Vitesse de groupe, vitesse de phase en prépa

Méthode 1. Calcul de $v_g$ et de $v_{\varphi}$ .

La vitesse de groupe est

$v_g=\frac{d\omega}{dk'}$

La vitesse de phase est

$v_{\varphi}=\frac{\omega}{k'}$

La vitesse de groupe est celle de propagation de l’enveloppe d’un paquet d’ondes ; la vitesse de phase est la vitesse de propagation d’un maximum de la porteuse à l’intérieur d’un paquet d’ondes. L’information se propage à la vitesse de groupe. Il est donc possible que la vitesse de phase dépasse la célérité de la lumière.

Exemple

La relation de dispersion dans le vide s’écrit $k=\frac{\omega}{c_0}$ . Exprimer les vitesses de groupe et de phase.

Méthode 2. Dispersion

Un milieu dispersif est caractérisé par une vitesse de phase qui dépend de la pulsation. Dans ce cas, les différentes composantes harmoniques du paquet d’ondes non monochromatique ne se propagent pas à la même vitesse. On observe alors l’étalement du paquet d’ondes.

Exemple

Le verre et l’eau sont des milieux transparents dispersifs pour les ondes électromagnétiques, leur vitesse de phase vaut

$v_{\varphi}=\frac{c_0}{n(\omega)}$

avec (loi de Cauchy)

$n(\omega)=A+B\omega^2$

Quel phénomène bien connu traduit cette propriété ?

Plasma maths spé : méthodes

Méthode 1. Traduire les hypothèses du plasma pour définir sa loi constitutive.

Un plasma est supposé neutre, dilué, peu dense, non relativiste.

* Il est neutre donc $\rho=0$

* On néglige le poids de l’électron devant la force électrique qu’il subit.

* Il est dilué donc on néglige la force de frottement devant la force électrique.

* Il est dilué donc l’onde qui s’y propage est proche de l’onde dans le vide, donc en ordres de grandeur $E\simeq c_0 B$ . On en déduit, que

$\displaystyle{\frac{\|e\vec{v}\wedge\vec{B}\|}{\|e\vec{E}\|}\simeq\frac{v}{c_0}\ll 1}$ car les électrons sont non relativistes.

* Le PFD appliqué à l’électron donne donc

$m_e\frac{d\vec{v}}{dt}=-e\vec{E}$

* On passe en formalisme complexe, on définit la densité $n_0$ d’électrons par mètre cube et on néglige le courant ionique devant le courant électronique.

$\vec{\underline{j}}=n_0(-e)\vec{\underline{v}}=\frac{n_0e^2}{i\omega m}\vec{\underline{E}}$

donc $\vec{\underline{j}}=\underline{\gamma}\vec{\underline{E}}$

où $\underline{\gamma}$ est la conductivité complexe du plasma.

Exemple.

Quel est le rapport entre le courant ionique et le courant électronique pour un plasma d’hydrogène ?

Méthode 2. Équation de dispersion du plasma

On applique la méthode indiquée dans la partie 1 de cette fiche. On obtient après calculs

$\displaystyle{\underline{k}^2=\frac{\omega^2-\omega_p^2}{c_0^2}}$

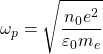avec $\displaystyle{\omega_p=\sqrt{\frac{n_0e^2}{\varepsilon_0m_e}}}$ pulsation plasma.

On distingue donc deux cas.

* Si $\omega<\omega_p$ , il y a une onde évanescente.

* Si $\omega>\omega_p$ , il y a propagation sans atténuation.

Exemple.

Exprimer la distance caractéristique d’atténuation de l’onde évanescente dans le cas $\omega<\omega_p$

Méthode 3. Propagation dans le plasma

On calcule aisément $v_g$ et $v_{\varphi}$ dans le plasma pour $\omega>\omega_p$ .

On constate que $v_g\cdot v_{\varphi}=c_0^2$ avec $v_g<c_0<v_{\varphi}$

On peut définir l’indice de réfraction du plasma $n=\frac{v_{\varphi}}{c_0}$ et faire une étude géométrique de propagation des rayons, mettre en évidence, en particulier, un angle limite de réfraction.

Exemple.

Donner les expressions des vitesses de groupe et de phase dans le plasma dans le cas $\omega>\omega_p$

Pour plus de cours et plus d’exercices, découvrez les autres cours en ligne de physique-chimie en PSI, les cours en ligne de physique-chimie en PT ainsi que les cours en ligne de physique-chimie en MP sur le site. Pour ce qui est des PC, les cours en ligne de physique en PC et les cours en ligne de PC en chimie sont également disponibles.

OEM dans les conducteurs ohmiques

Méthode 1. Équations de Maxwell dans un conducteur ohmique en régime lentement variable

Le « régime lentement variable » correspond à des fréquences inférieures à $10^{15}~\mathrm{Hz}$ environ pour un bon conducteur ohmique de conductivité

$\gamma\simeq 10^7~\mathrm{S\cdot m^{-1}}$

Sous cette hypothèse, le milieu est localement neutre, et le courant de déplacement est négligeable devant le courant électronique.

On en déduit

$\mathrm{div}\vec{E}=0$ et $\mathrm{div}\vec{B}=0$

$\displaystyle{\vec{\mathrm{rot}}\vec{E}=-\frac{\partial\vec{B}}{\partial t}}$

et $\displaystyle{\vec{\mathrm{rot}}\vec{B}=\mu_0\vec{j}=\mu_0\gamma\vec{E}}$

Exemple

Vérifier la négligeabilité du courant de déplacement devant le courant électronique avec les valeurs proposées.

On donne $\varepsilon_0=8,854\cdot 10^{-12}~\mathrm{F\cdot m^{-1}}$

Méthode 2. Équation de dispersion dans le conducteur ohmique, effet de peau

On applique la méthode indiquée dans la partie 1 de cette fiche. On obtient après calculs

$\displaystyle{\underline{k}^2=-i\mu_0\gamma\omega}$

donc en gardant la solution de partie réelle positive

$\displaystyle{\underline{k}=\sqrt{\frac{\mu_0\gamma\omega}{2}}-i\sqrt{\frac{\mu_0\gamma\omega}{2}}}$

Il y a donc propagation atténuée avec une distance caractéristique d’atténuation appelée épaisseur de peau

$\displaystyle{\delta=-\frac1{k''}=\sqrt{\frac{2}{\mu_0\gamma\omega}}}$

Exemple.

Calculer l’épaisseur de peau pour une onde radio de fréquence $f=162~\mathrm{kHz}$ dans un conducteur ohmique de conductivité $\gamma=1,0\cdot 10^6~\mathrm{S\cdot m^{-1}}$ . On donne $\mu_0=4\pi\cdot 10^{-7}~\mathrm{H\cdot m^{-1}}$

Révisez, entrainez-vous et vérifiez vos connaissances sur les autres chapitres au programme de physique-chimie en maths spé, pour être sûr de réussir les concours :

Cours sur ondes électromagnétiques dans les milieux en MPI, MP, PSI, PC et PT

Pseudo-OPPH en maths spé

Méthode 1 : pseudo-OPPH.

Méthode 2. Équation de dispersion

Vitesse de groupe, vitesse de phase en prépa

Méthode 1. Calcul de $v_g$ et de $v_{\varphi}$ .

Méthode 2. Dispersion

Plasma maths spé : méthodes

Méthode 1. Traduire les hypothèses du plasma pour définir sa loi constitutive.

Méthode 2. Équation de dispersion du plasma

Méthode 3. Propagation dans le plasma

OEM dans les conducteurs ohmiques

Méthode 1. Équations de Maxwell dans un conducteur ohmique en régime lentement variable

Méthode 2. Équation de dispersion dans le conducteur ohmique, effet de peau

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales