Chapitres de maths en Terminale S2

Résumé de cours sur les probabilités en Terminale S2

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de maths en Terminale S2

1 – Probabilités conditionnelles en terminale S2

Soient des événements $A$ et $B$ . Si $A$ est de probabilité non nulle, alors la probabilité de $B$ sachant $A$ , notée $P_{A}(B)$ , est définie par :

${P_{A}(B)=\dfrac{P(A \cap B)}{P(A)}$

Des événements $A$ et $B$ sont dits indépendants si et seulement si ${P(A \cap B) = P(A) \times P(B)$ .

Théorème

Soient des événements $A$ et $B$ de probabilités non nulles. Les trois assertions suivantes sont équivalentes :

(i) $P_{A}(B)=P(B)$

(ii) $P(A \cap B) = P(A) \times P(B)$

(iii) $P_{B}(A)=P(A)$

Définition : indépendance de deux variables aléatoires

Soient deux variables aléatoires $X$ et $Y$ définies sur $E$ .

On note $x_{1}, x_{2},..., x_{k}$ les valeurs prises par $X$ et $y_{1}, y_{2},...,y_{r}$ celles prises par $Y$ .

$X$ et $Y$ sont dites indépendantes si et seulement si, pour tout $i$ de $\{1,2,...,k\}$ et tout $j$ de $\{1,2,...,r\}$ :

$P(X=x_{i}$ et $Y=y_{j})$

$= P(X=x_{i}) \times P(Y=y_{j})$

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

2 – Combinaisons et formule du binôme en terminale S2

Soit $E$ un ensemble de cardinal $n$ , soit $p$ un entier naturel

$\bullet$ Une combinaison de $p$ éléments de $E$ est une partie de $E$ possédant $p$ éléments. On note $\begin{pmatrix} n \\ p \\ \end{pmatrix}$ le nombre de combinaisons de $p$ éléments de $E$ .

$\bullet$ Si $p=0$ , alors $\begin{pmatrix} n \\ 0 \\ \end{pmatrix} = 1$ .

$\bullet$ Si $0 < p \leq n$ , alors : $\begin{pmatrix} n \\ p \\ \end{pmatrix} = \displaystyle{\frac{n (n-1)\times ... \times (n-p+1)}{p (p-1) \times ... \times 2 \times 1}}$

= $\displaystyle{\frac{n!}{p!(n-p)!}}$ .

Propriétés

$\bullet$ Pour tout entier naturel $n$ : $\begin{pmatrix} n \\ 0 \\ \end{pmatrix} = \begin{pmatrix} n \\ n \\ \end{pmatrix} = 1$ et si $n \geq 1$ : $\begin{pmatrix} n \\ 1 \\ \end{pmatrix} = \begin{pmatrix} n \\ n-1 \\ \end{pmatrix} = n$ .

Pour tous entiers naturels $n$ et $p$ tels que $p \leq n$ , on a : $\begin{pmatrix} n \\ p \\ \end{pmatrix} = \begin{pmatrix} n \\ n-p \\ \end{pmatrix}$ .

Formule de Pascal : pour tous entiers naturels $n$ et $p$ tels que $p < n$ , on a :

${\begin{pmatrix} n+1 \\ p+1 \\ \end{pmatrix} = \begin{pmatrix} n \\ p \\ \end{pmatrix} + \begin{pmatrix} n \\ p+1 \\ \end{pmatrix}$

Formule du binôme de Newton

Pour tous complexes (et donc réels) $a$ et $b$ , et tout entier naturel non nul $n$ :

$(a+b)^{n}$ =

$a^{n} + \begin{pmatrix} n \\ 1 \\ \end{pmatrix} a^{n-1}b^{1} + ... + \begin{pmatrix} n \\ k \\ \end{pmatrix} a^{n-k}b^{k} + ... + \begin{pmatrix} n \\ n-1 \\ \end{pmatrix} a^{1}b^{n-1} + b^{n} = \sum_{k=0}^{n} \begin{pmatrix} n \\ k \\ \end{pmatrix} a^{n-k}b^{k}$

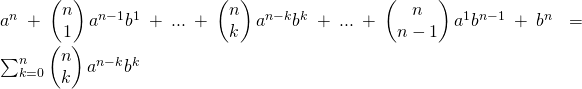
COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

3 – Lois de Bernouilli et binomiale terminale S2

Loi de Bernoulli

Une variable aléatoire $X$ , prenant la valeur $1$ avec la probabilité $p$ et la valeur $0$ avec la probabilité $1-p$ , suit la loi de Bernoulli de paramètre $p$ .

On notera alors :

${X \thicksim B(p)$

L’espérance et la variance d’une variable aléatoire de Bernoulli de paramètre $p$ sont données par :

${E(X)=p\text{ et }Var(X)=p(1-p)$

Loi binomiale

La somme $X$ de $n$ variables aléatoires indépendantes de Bernoulli, prenant la valeur $1$ avec la probabilité $p$ et la valeur $0$ avec la probabilité $1-p$ , suit la loi binomiale de paramètre $(n,p)$ .