Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Convergences et approximations en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Méthodes – Inégalités & convergences de suites de variables aléatoires
Méthode 1 : Savoir utiliser l’inégalité de Markov.
On rappelle l’inégalité de Markov : si ![]() est une variable aléatoire positive ayant une espérance, alors pour tout
est une variable aléatoire positive ayant une espérance, alors pour tout ![]() on a
on a
![]()
![]()
L’inégalité de Markov sert souvent à établir des inégalités à condition de reconnaître la loi d’une variable aléatoire classique à valeurs positives.
Exemple : Soit ![]() Montrer que pour tout
Montrer que pour tout ![]()
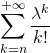
![]()
Réponse :
On introduit ![]() une variable aléatoire suivant une loi de Poisson de paramètre
une variable aléatoire suivant une loi de Poisson de paramètre ![]()
![]() est à valeurs positives et admet une espérance égale à
est à valeurs positives et admet une espérance égale à ![]()
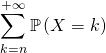
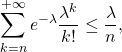 il suffit de multiplier par
il suffit de multiplier par
Méthode 2 : Savoir utiliser l’inégalité de Bienaymé-Tchebychev.
Soit ![]() une variable aléatoire ayant une variance. Alors, pour tout
une variable aléatoire ayant une variance. Alors, pour tout ![]()
![]()
![]()
Cette inégalité servira notamment dans les méthodes suivantes lorsque l’on parlera de convergence de suites de variables aléatoires.
Exemple : Soit ![]() une variable aléatoire d’espérance
une variable aléatoire d’espérance ![]() et de variance
et de variance ![]() Montrer que, pour tout
Montrer que, pour tout ![]()
![]()
![]()
Réponse : On applique l’inégalité de Bienaymé-Tchebychev à ![]() cela donne :
cela donne :
On conclut en passant à l’événement complémentaire.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 3 : Sur la convergence en probabilité.
On rappelle qu’une suite de variables aléatoires ![]() converge en probabilité vers une variable aléatoire
converge en probabilité vers une variable aléatoire ![]() si : pour tout
si : pour tout ![]()
![]()
![]()
On écrit ![]()
Les inégalités de Markov et de Bienaymé-Tchebychev sont très utiles pour montrer la convergence en probabilité.
Méthode 4 : Sur la convergence en loi.
On suppose que pour tout ![]()
![]() est une variable aléatoire réelle définie sur
est une variable aléatoire réelle définie sur ![]() de fonction de répartition
de fonction de répartition ![]() et que
et que ![]() une variable aléatoire réelle définie sur le même espace probabilisé dont on note
une variable aléatoire réelle définie sur le même espace probabilisé dont on note ![]() la fonction de répartition.
la fonction de répartition.
On dit que la suite de variables aléatoires ![]() converge vers
converge vers ![]() en loi si
en loi si
![]()
![]()
en tout point ![]() où
où ![]() est continue. On écrit
est continue. On écrit ![]()
Dans le cas où les variables aléatoires ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() il est plus simple d’utiliser la caractérisation suivante : la suite de variables aléatoires
il est plus simple d’utiliser la caractérisation suivante : la suite de variables aléatoires ![]() converge en loi vers
converge en loi vers ![]() si et seulement si,
si et seulement si,
pour tout ![]()
![]()
![]()
On retiendra le résultat suivant au programme :
Soit ![]() et
et ![]() une suite de réels de
une suite de réels de ![]() telle que
telle que ![]()
![]() On suppose que tout
On suppose que tout ![]()
![]() suit une loi binomiale de paramètres
suit une loi binomiale de paramètres ![]() et
et ![]()
Alors ![]() converge en loi vers une variable aléatoire de loi de Poisson de paramètre
converge en loi vers une variable aléatoire de loi de Poisson de paramètre ![]()
Méthode 5 : Utiliser le théorème central limite pour des variables aléatoires binomiales ou de loi de Poisson.
On rappelle l’énoncé :
Si ![]() est une suite de variables aléatoires telle que
est une suite de variables aléatoires telle que ![]() suit une loi binomiale
suit une loi binomiale ![]() (respectivement
(respectivement ![]() de loi
de loi ![]() ), alors la suite de variables aléatoires centrées réduites
), alors la suite de variables aléatoires centrées réduites ![]() converge en loi vers une variable aléatoire suivant la loi normale centrée réduite.
converge en loi vers une variable aléatoire suivant la loi normale centrée réduite.
On rappelle que ![]()
Le théorème dit que
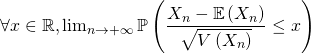
![]()
Si ![]() suit une loi
suit une loi ![]()
![]()
![]()
Si ![]() suit une loi
suit une loi ![]() on a
on a
![]()
![]()
Exemple : Dans un stade, il y a ![]() supporters. On estime qu’un supporter mange un sandwich avec une probabilité de
supporters. On estime qu’un supporter mange un sandwich avec une probabilité de ![]() et le choix de manger un sandwich ou non ne dépend pas de ce que font les autres supporters.
et le choix de manger un sandwich ou non ne dépend pas de ce que font les autres supporters.
Combien le club doit-il acheter de sandwichs pour que la probabilité qu’il y ait rupture de stock soit inférieur à ![]() ?
?
Indications :
![]() On admettra que l’on peut approcher une loi binomiale de paramètres
On admettra que l’on peut approcher une loi binomiale de paramètres ![]() et
et ![]() par une loi normale
par une loi normale ![]() lorsque
lorsque ![]()
![]() et
et ![]()
![]() On utilisera le fait suivant : si
On utilisera le fait suivant : si ![]() suit la loi normale centrée réduite et
suit la loi normale centrée réduite et ![]() ,
,
![]()
![]()
Réponse :
Soit ![]() le nombre de sandwichs demandés par les supporters.
le nombre de sandwichs demandés par les supporters. ![]() suit une loi binomiale de paramètres
suit une loi binomiale de paramètres ![]() et
et ![]()
Ainsi, il suffit de trouver
Il suffit que le stade achète environ ![]() sandwichs.
sandwichs.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
De multiples autres chapitres de maths en ECG1 peuvent être revus et travaillés depuis chez vous avec nos différents cours en ligne au programme d’ECG1 :

