Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés – Convergences et approximations en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Inégalités classiques, convergences de suites de variables aléatoires
Exercice :
1) a) ![]()
![]()
b) La fonction ![]() est continue sur
est continue sur ![]() à valeurs positives et
à valeurs positives et ![]() ; comme l’intégrale
; comme l’intégrale ![]() converge, on en déduit que l’intégrale
converge, on en déduit que l’intégrale ![]() est convergente.
est convergente.
c) On a ![]()
![]()
d) Soit ![]() On fait une intégration par parties sur
On fait une intégration par parties sur ![]() en utilisant les fonctions de classe
en utilisant les fonctions de classe ![]()
![]() et
et ![]() On a
On a
![Rendered by QuickLaTeX.com = \left[ \dfrac{- \left( \ln \left( 1 + t \right) \right)^{n + 1}}{1 + t} \right]_0^x](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0ddced627a2214311da20a01fe92d7c8_l3.png)
Puis si
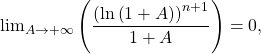 on obtient
on obtient COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2) a) ![]() est continue sur
est continue sur ![]() (on vérifie qu’elle est bien continue en
(on vérifie qu’elle est bien continue en ![]() car les limites à droite et à gauche de
car les limites à droite et à gauche de ![]() sont égales à
sont égales à ![]() ),
), ![]() est à valeurs positives, l’intégrale
est à valeurs positives, l’intégrale ![]() converge et est égale à
converge et est égale à ![]()
![]()
b) La fonction ![]() est continue sur
est continue sur ![]()
Pour ![]()
![]()
![]() l’intégrale
l’intégrale ![]() diverge car
diverge car ![]() donc l’intégrale
donc l’intégrale ![]() diverge. La variable
diverge. La variable ![]() n’a pas d’espérance.
n’a pas d’espérance.
c) Comme ![]() est nulle sur
est nulle sur ![]() pour
pour ![]()
![]()
d) Pour ![]()
![]()
![]()
![]()
![]()
![]()
e) Soit ![]() et
et ![]() en intégrant par parties en utilisant les fonctions
en intégrant par parties en utilisant les fonctions ![]() sur
sur ![]()
![]() et
et ![]() avec
avec ![]()
![Rendered by QuickLaTeX.com = \left[ - \dfrac{\left( \ln \left( 1 + t \right) \right)^k}{k! \left( 1 + t \right)} \right]_0^x](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7f79c80198db2fe5c9f168837c957b94_l3.png)
On obtient alors
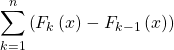
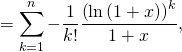
soit
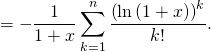 Or
Or 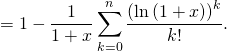
f) Pour ![]() on reconnaît une somme partielle d’une série exponentielle, donc
on reconnaît une somme partielle d’une série exponentielle, donc 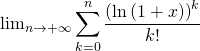
![]()
![]() et
et ![]()
g) La limite de la suite de fonctions de répartitions ![]() n’est pas une fonction de répartition, donc la suite de variables aléatoires
n’est pas une fonction de répartition, donc la suite de variables aléatoires ![]() ne converge pas en loi.
ne converge pas en loi.
3) a) ![]() est une variable aléatoire à valeurs dans
est une variable aléatoire à valeurs dans ![]() donc on peut définir la variable aléatoire
donc on peut définir la variable aléatoire ![]() et
et ![]() est à valeurs positives.
est à valeurs positives.
b) Si ![]()
![]()
![]()
![]()
c) On a montré que la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() de dérivée égale à
de dérivée égale à ![]() (la fonction
(la fonction ![]() est continue sur
est continue sur ![]() ), donc par composée, la fonction
), donc par composée, la fonction ![]() est de classe
est de classe ![]() sur
sur ![]()
![]() admet une densité
admet une densité ![]()
d) La fonction ![]() est continue sur
est continue sur ![]() nulle sur
nulle sur ![]() à valeurs positives et vérifie
à valeurs positives et vérifie ![]() donc l’intégrale
donc l’intégrale ![]() est absolument convergente.
est absolument convergente.
e) On montre de même que l’intégrale ![]() est convergente et que
est convergente et que
Alors
f) ![]() suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre ![]() Pour tout
Pour tout ![]() on a
on a
![]()
![]()
![]()
g) ![]()
![]()
![]() et
et ![]()
![]()
![]()
Par encadrement,
La suite de terme général ![]() converge en probabilité vers une variable aléatoire constante égale à
converge en probabilité vers une variable aléatoire constante égale à ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Grâce à ces exercices et à ces corrigés d’exercices, vos points forts et vos points faibles en maths en ECG1 se feront vite connaître. Profitez-en pour cibler vos révisons et vos entraînements sur les notions qui sont le plus difficiles pour vous. Les cours suivants doivent également être bien maîtrisés :

