Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés : Intégration en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Intégration
Exercice 1 :
1) L’expression ![]() (de la forme
(de la forme ![]() ) se primitive en
) se primitive en ![]() ainsi
ainsi
![]()
2) Commençons par linéariser ![]() On utilise la formule de Moivre-Euler
On utilise la formule de Moivre-Euler
![]()
![]()
![]()
![]() .
.
D’où
![]()
![Rendered by QuickLaTeX.com = \left[ \dfrac{\sin \left( 4 t \right)}{32} + \dfrac{\sin \left( 3 t \right)}{6} + \dfrac38 t \right]_0^{\dfrac{\pi}{2}} .](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d2c5417ba769ee3a077b5f3e0ae0589b_l3.png)
3) On écrit
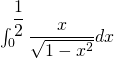
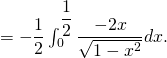
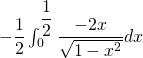
![Rendered by QuickLaTeX.com = -\dfrac12 \left[ 2 \sqrt{1 - x^2} \right]_0^{\dfrac12}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-371108fae56e4b6af9df08533c797240_l3.png)
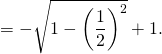
![]()
![]()
Exercice 2 :
1) Si l’on pose ![]() on commence par remplacer
on commence par remplacer ![]() par
par ![]() on a donc :
on a donc :
![]()
On exprime ![]() en fonction de
en fonction de ![]() Comme
Comme ![]() on a
on a ![]() soit
soit ![]() ainsi
ainsi
![]()
Il nous reste à trouver les bonne bornes : lorsque ![]() et lorsque
et lorsque ![]() d’où finalement :
d’où finalement :
![]()
Cette dernière est plus facile à calculer car ![]() se primitive en
se primitive en ![]() d’où :
d’où :
![Rendered by QuickLaTeX.com \[\int_{0}^{\dfrac{\pi}{2}} \cos^2 \left( \theta \right) d \theta.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-91df4d3daa35bd8281ff0f65516e3bea_l3.png)
Pour calculer cette intégrale, il faut linéariser ![]() On utilise les formules de Moivre-Euler :
On utilise les formules de Moivre-Euler :![]()
![]()
![]()
![]() .
.
Ainsi
![Rendered by QuickLaTeX.com \[\int_{0}^{\dfrac{\pi}{2}} \cos^2 \left( \theta \right) d \theta = \int_0^{\dfrac{\pi}{2}} \dfrac{\cos \left( 2 \theta \right) + 1}{2} d \theta = \dfrac{\pi}{4}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4e853ee9788350faddd9509d4a374f6b_l3.png)
Exercice 3 :
1) On a
![]()
![Rendered by QuickLaTeX.com = \left[ - \dfrac{ \left( b - t \right)^{q + 1} }{q + 1} \right]_a^b](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2699c46df37f178b4dc83734419d3998_l3.png)
2) On fait une intégration par parties en posant ![]() et
et ![]() Les fonctions
Les fonctions ![]() et
et ![]() sont
sont ![]() sur
sur ![]() et :
et :
![Rendered by QuickLaTeX.com = \left[ - \dfrac{\left( t - a \right)^p \left( b - t \right)^{q + 1} }{q + 1} \right]_a^b](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-653c25261e026853cd713d760913dd1e_l3.png)
![Rendered by QuickLaTeX.com \left[ - \dfrac{\left( t - a \right)^p \left( b - t \right)^{q + 1} }{q + 1} \right]_a^b = 0,](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2c957322020f76dcb819fe41963bc901_l3.png) on a
on a 3) Si l’on applique ![]() fois (avec
fois (avec ![]() ) la relation précédente, on a :
) la relation précédente, on a :
En prenant
![]()
Comme ![]() d’où finalement
d’où finalement
![]()
Exercice 4 :
1) On calcule
Comme
2) On encadre ![]() par deux suites ayant
par deux suites ayant ![]() pour limite.
pour limite.
3) On une intégration par parties en posant ![]() et
et ![]()
![]() et
et ![]() sont
sont ![]() sur
sur ![]() on a donc
on a donc
En procédant comme ci-dessus, on montre que
![]()
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut


