Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés : Matrices en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Matrices
Exercice 1 :
On remarque que ![]() où
où 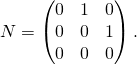 On remarque que
On remarque que 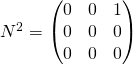 et
et ![]() Comme
Comme ![]() et
et ![]() commutent, on peut appliquer la formule du binôme de Newton, d’où pour
commutent, on peut appliquer la formule du binôme de Newton, d’où pour ![]()
![]()
![]()
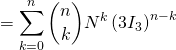
![]()
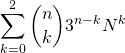
![]() .
.
On vérifie que cette formule est vraie pour ![]() et
et ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 :
1) Pour ![]() on pose
on pose
![]() : « il existe
: « il existe ![]() tel que
tel que 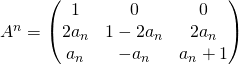 « .
« .
![]() Pour
Pour ![]() on a
on a ![]() ainsi
ainsi ![]() est vraie avec
est vraie avec ![]()
![]() Supposons
Supposons ![]() est vraie, montrons que
est vraie, montrons que ![]() est vraie. Pour cela, écrivons :
est vraie. Pour cela, écrivons :
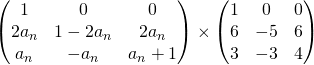
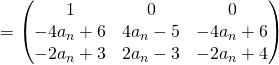
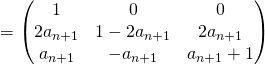 ,
,2) Nous avons montré que la suite ![]() vérifie
vérifie ![]() et
et ![]() La suite
La suite ![]() est donc arithmético-géométrique.
est donc arithmético-géométrique.
Le cours donne ![]()
On en déduit ![]() en remplaçant
en remplaçant ![]() dans
dans ![]()
Exercice 3 : Calcul de produit scalaire
1) Soit ![]() L’ensemble
L’ensemble ![]() est une partie non vide de
est une partie non vide de ![]() car
car ![]() est nilpotente. Donc
est nilpotente. Donc ![]() admet un plus petit élément
admet un plus petit élément ![]() Comme
Comme ![]() on a
on a ![]()
Si ![]() cela signifierait que
cela signifierait que ![]() et que
et que ![]() n’est pas le plus petit élément de
n’est pas le plus petit élément de ![]()
Ainsi, on a ![]() et
et ![]()
2) On suppose ![]() inversible, il existe donc
inversible, il existe donc ![]() telle que
telle que ![]()
En multipliant par ![]() :
: ![]() donc
donc ![]() ce qui est impossible par choix de
ce qui est impossible par choix de ![]()
La matrice ![]() n’est pas inversible.
n’est pas inversible.
3) On a, pour tout ![]()
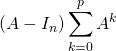
![]()
![]()
![]()
![]() .
.
![Rendered by QuickLaTeX.com \[- I_n = \left( A - I_n \right) \displaystyle\sum_{k=0}^p A^k,\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7e7389d32d60da12e2f19750b31bf410_l3.png)
d’où ![]() est inversible et
est inversible et
![Rendered by QuickLaTeX.com \[\left( I_n - A \right)^{- 1} = \displaystyle\sum_{k=0}^p A^k.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-52f928056dc97023e4d4b70c7e2191a4_l3.png)
Exercice 4 :
1) ![]() Pour une matrice
Pour une matrice ![]() on a
on a
![]()
soit
![]()
Cela peut se réécrire sous la forme
![]()
Ainsi ![]() est inversible et
est inversible et ![]()
![]() Cette matrice étant de taille
Cette matrice étant de taille ![]() il n’y a pas de formule analogue à celle obtenue pour les matrices
il n’y a pas de formule analogue à celle obtenue pour les matrices ![]() (en fait, si mais elle est compliquée).
(en fait, si mais elle est compliquée).
Soit 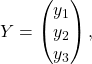 cherchons
cherchons 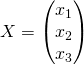 tel que
tel que ![]() Cela donne le système suivant :
Cela donne le système suivant :
![Rendered by QuickLaTeX.com \[\begin{cases} x_3 = y_1 \\ x_2 = y_2 \\ x_1 = y_3 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7dd8a7e619d44b14ed74213efaf0398f_l3.png)
Ainsi
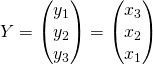
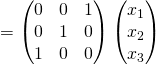
![]()
Ainsi ![]() est inversible et
est inversible et ![]()
![]() On procède de la même manière : soit
On procède de la même manière : soit 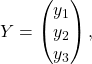 cherchons
cherchons 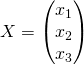 tel que
tel que ![]() Cela donne le système suivant :
Cela donne le système suivant :
![Rendered by QuickLaTeX.com \[\begin{cases} x_1 - x_2 & = y_1 \\ x_1 + 2 x_2 + x_3 & = y_2 \\ x_1 + x_2 & = y_3 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-026bd08c9e01d2d09a478649cd425fff_l3.png)
On applique la méthode du pivot de Gauss. On commence par faire ![]() et
et ![]() pour obtenir
pour obtenir
![Rendered by QuickLaTeX.com \[\begin{cases} x_1 - x_2 & = y_1 \\ 3 x_2 + x_3 & = y_2 - y_1 \\ 2 x_2 & = y_3 - y_1 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3ba4e5d606a735849854ddc370da367b_l3.png)
la dernière ligne donne directement ![]() La deuxième ligne donne
La deuxième ligne donne
![]()
La première ligne donne finalement
![]()
On a
![]()
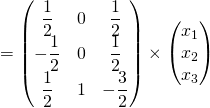
![]() .
.
Soit
![Rendered by QuickLaTeX.com \[C^{-1} = \begin{pmatrix} \dfrac12 & 0 & \dfrac12 \\ - \dfrac12 & 0 & \dfrac12 \\ \dfrac12 & 1 & - \dfrac32 \end{pmatrix}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ab01f1cfde1faef83c4015aacddbbb42_l3.png)
2) ![]() La première colonne étant nulle, on a
La première colonne étant nulle, on a ![]() ainsi
ainsi
![Rendered by QuickLaTeX.com \[E \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3263c94c49a51eb60b3457317b8b7170_l3.png)
donc ![]() n’est pas inversible.
n’est pas inversible.
![]() On remarque que
On remarque que ![]() ainsi
ainsi 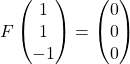 et donc
et donc ![]() n’est pas inversible.
n’est pas inversible.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Retrouvez d’autres corrigés sur chacun de nos cours en ligne au programme de maths pour les ECG1 :

