Chapitres Maths en ECG1

Corrigés : Polynômes en ECG1

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices Corrigés

Cours en ligne de Maths en ECG1

Corrigés sur les Polynômes en ECG1

Exercice 1 :

1) On pose $A= 3X^5 + 4X^2 + 1$ et $B = X^2 - 4 X + 3.$ Comme $B \neq 0,$ il existe $Q \in \mathbb{R} \left[ X \right]$ et $R$ tel que $\deg \left( R \right) < \deg \left( B \right) = 2$ (il existe donc $a, b \in \mathbb{R}$ tels que $R = a X + b$ ) et $A = B Q + R.$

Remarquons que $B$ se factorise en $\left( X - 1 \right) \left( X - 3\right).$

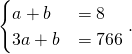Évaluons la relation en les racines de $B$ : $1$ et $3.$ On a le système suivant : $\begin{cases} a + b & = 8 \\ 3 a + b & = 766 \end{cases}.$ La résolution de ce système donne $a = 379$ et $b = -371.$

Ainsi $R = 379 X - 371.$

2) On commence par remarquer que $X^2 - 3 X + 2 = \left( X - 1 \right) \left( X - 2 \right).$ Soit $R$ le reste de la division euclidienne de $X^n$ par $X^2 - 3 X + 2.$ Comme $\deg \left( X^2 - 3X + 2 \right)= 2,$ $R$ est un polynôme de degré au plus $1.$ Ainsi, on peut écrire $R = aX + b$ avec $a, b \in \mathbb{R}.$ Il existe donc $Q \in \mathbb{R} \left[ X \right]$ tel que

$X^n = Q \left( X - 1 \right) \left( X - 2 \right) + R.$

En évaluant cette relation en $1$ et $2,$ on a le système suivant d’équations :

$\begin{cases} 1 & = a + b \\ 2^n & = 2 a + b \end{cases}.$

La résolution donne $a=2^n - 1$ et $b = 2 - 2^n.$

Ainsi

$R= \left( 2^n - 1 \right) X + 2 - 2^n.$

3) $\bullet$ On écrit $X^{2n } + 2 X^n + 1 = Q \left( X^2 + 1 \right) + R.$

Comme $\deg \left( X^2 + 1 \right) = 2,$ le reste est de degré au plus $1,$ on écrit donc $R= a X + b.$

En évaluant en les racines de $X^2 + 1,$ qui sont $i$ et $-i,$ on obtient le système suivant :

$\begin{cases} a i + b & = i^{2n} + 2 i^n + 1 \\ - ai + b & = \left( - i \right)^{2n} + 2 \left( - i \right)^n + 1 \end{cases}.$

Remarquons que la seconde ligne se retrouve grâce à la première en conjuguant. Ainsi, on doit trouver $a , b \in \R$ tels que $ai + b = i^{2n} + 2 i^n + 1 = \left( \left( - 1 \right)^n + 1 \right) + 2 i^n.$ Il faut discuter selon les valeurs de $n$ :

$\star$ si $n = 4 k$ avec $k \in \mathbb{N},$ alors on a : $ai + b = 4$ soit $a=0,$ $b = 4,$ donc $R = 4.$

$\star$ si $n = 4 k + 1$ avec $k \in \mathbb{N},$ alors on a : $a i + b = 2i$ soit $a = 2,$ $b = 0,$ donc $R= 2 X.$

$\star$ si $n = 4 k + 2$ avec $k \in \mathbb{N},$ alors on a : $a i + b = 0$ soit $a = b = 0,$ donc $R=0.$

$\star$ si $n = 4 k + 3$ avec $k \in \mathbb{N},$ alors on a : $a i + b = - 2i$ soit $a=- 2, b = 0$ donc $R= - 2X.$

$\bullet$ On écrit $X^{2n}+ X^n + 1 = Q \left( X - 1 \right)^2 + R .$ Comme $\deg \left( \left( X - 1 \right)^2 \right) = 2,$ le reste est de degré au plus $1,$ on écrit donc $R = a X + b.$ Puis on traduit que $S= X^{2n} + X^n +1 - R$ est divisible par $\left( X - 1 \right)^2$ ce qui revient à dire que $S \left( 1 \right) = S ' \left( 1 \right) = 0$ . On obtient le système suivant

$\begin{cases} 4 - a - b & = 0 \\ 2n + 2n & = a \end{cases} \Leftrightarrow \begin{cases} b = 4 \left( 1- n \right) \\ a = 4n \end{cases}.$

Le reste est égal à $4 n X + 4 - 4n.$

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Exercice 2 :

Soit $P$ un polynôme vérifiant les conditions de l’énoncé. Comme $3 + 2i$ est racine de $P$ , polynôme à coefficients réels, on en déduit que $3 - 2i$ est aussi racine de même ordre que $3 + 2i,$ c’est-à-dire $1.$

Résumons : $1$ est racine d’ordre $2$ donc $P$ est divisible par $\left( X - 1 \right)^2,$ $2$ est racine d’ordre $1$ donc $X - 2$ divise $P,$ $3 + 2i$ est racine d’ordre $1$ donc $X - \left( 3 + 2i \right)$ divise $P$ et enfin $3 - 2i$ est racine d’ordre $1$ donc $X - \left( 3 - 2i \right)$ divise $P.$

Remarquons que comme $\deg \left( P \right) = 5,$ on a toutes les racines (comptées avec l’ordre de multiplicité). Si bien que $P$ $= 3 \left( X - 1 \right)^2 \left( X - 2 \right) \left( X - \left( 3 + 2i \right) \right) \left( X - \left( 3 - 2i \right) \right)$ (attention à ne pas oublier le coefficient dominant).

On laisse le soin au lecteur de développer (ou pas) l’expression.

Exercice 3 :

1) Comme $\left( X - 1 \right)^3$ divise $P - 1,$ il existe un polynôme $Q$ tel que $P - 1 = \left( X - 1 \right)^3 Q .$ Comme $\deg \left( P - 1 \right) = 5,$ alors $\deg \left( Q \right) = 2.$

2) Soit $R = P + 2.$

Le polynôme $\left( X - 2 \right)^3$ divise $R$ si, et seulement si, $R \left( 2 \right) = R ' \left( 2 \right) = R'' \left( 2 \right) =0$ (voir \textbf{méthode 2.8}).

On obtient donc les conditions nécessaires et suffisantes $P \left( 2 \right) = - 2, P ' \left( 2 \right) = 0$ et $P '' \left( 2 \right) = 0.$

3) On utilise la relation $P = \left( X - 1 \right)^3 Q + 1.$

On a
$P' = 3 \left( X - 1 \right)^2 Q + \left( X - 1 \right)^3 Q '$ et $P ''$ $= 6 \left( X - 1 \right) Q + 6 \left( X - 1 \right)^2 Q ' + \left( X - 1 \right)^3 Q''.$

$P \left( 2 \right) = Q \left( 2 \right) + 1, P ' \left( 2 \right)$ $= 3 Q \left( 2 \right) + Q ' \left( 2 \right) \, \text{et} \, P '' \left( 2 \right)$ $= 6 Q \left( 2 \right) + 6 Q ' \left( 2 \right) + Q '' \left( 2 \right).$
Les conditions $P \left( 2 \right) = - 2, P ' \left( 2 \right) = P'' \left( 2 \right) =0$ donnent

$\begin{cases} Q \left( 2 \right) & = - 3 \\ Q ' \left( 2 \right) = - 3 Q \left( 2 \right) & = 9 \\ Q '' \left( 2 \right) = - 6 Q \left( 2 \right) - 6 Q ' \left( 2 \right) & = - 36 \end{cases}$

$\Leftrightarrow \begin{cases} 4 a + 2 b + c & = - 3 \\ 4a + b & = 9 \\ 2 a & = -36 \end{cases}$

$\Leftrightarrow \begin{cases} c & = - 93 \\ b & = 81 \\ a & = -18 \end{cases}.$

On obtient donc

$P = \left( X - 1\right)^3 \left( - 18 X^2 + 81 X - 93 \right) + 1$ soit

$P = - 18 X^5 + 135 X^4 - 390 X^3 + 540 X^2$

$- 360 X + 94.$

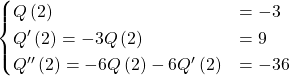
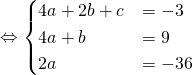
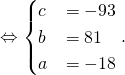
Exercice 4 :

Pour montrer que $\left( X - 1 \right)^2$ divise $P_n = 2X^{n + 2} - \left( n + 2 \right) X^2 + n,$ il suffit de montrer que $P_n \left( 1 \right) = P_n ' \left( 1 \right) = 0.$

On a bien $P_n \left( 1 \right) = 2 - \left( n + 2 \right) + n =0.$

Comme $P_n ' = 2 \left( n + 2 \right) X^{n + 1} - 2 \left( n + 2 \right) X,$ on a bien $P_n ' \left( 1 \right) = 0.$

Exercice 5 :

Remarquons que le polynôme nul est solution. On procède par analyse-synthèse :

Analyse : Soit $P$ une solution (éventuelle) non nulle. On pose $d = \deg \left( P \right).$ Comme $P \left( X^2 \right) = \left( X^2 + 1 \right) P \left( X \right),$ $d$ vérifie $2d = 2 + d,$ on a $d = 2.$ On pose $P = a X^2 + b X + c$ où $a, b$ et $c$ sont des réels.

L’équation $P \left( X^2 \right) = \left( X^2 + 1 \right) P \left( X \right)$ donne

$a X^4 + b X^2 + c = \left( X^2 + 1 \right) \left( a X^2 + b X + c \right) = a X^4 + b X^3 + \left( a + c \right) X^2 + bX + c.$

Par égalité de deux polynômes, on a

$\begin{cases} a & = a \\ 0 & = b \\ b & = a + c \\ 0 & = b \\ c & =c \end{cases}.$

Ainsi $b = 0$ et $-a = c.$ D’où $P = a X^2 - a = a \left( X^2 - 1 \right).$

Synthèse : La synthèse est facile : les polynômes de la forme $a \left( X^2 - 1 \right)$ avec $a \in\mathbb{R}$ vérifient bien l’équation $P \left( X^2 \right) = \left( X^2 + 1 \right) P \left( X \right).$

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION