Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés d’exercices : Probabilités sur un univers fini en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Probabilités sur un univers fini
Exercice 1 :
1) Par définition, il y a ![]() tirages possibles.
tirages possibles.
2) a) Comme on veut que toutes les boules aient un numéro inférieur à ![]() cela revient à tirer
cela revient à tirer ![]() boules dans l’ensemble
boules dans l’ensemble ![]() il y a
il y a ![]() tirages possibles.
tirages possibles.
b) Pour obtenir un tirage de ![]() boules dont le plus grand numéro est égal à
boules dont le plus grand numéro est égal à ![]() on choisit
on choisit ![]() boules parmi les boules numérotées de
boules parmi les boules numérotées de ![]() à
à ![]() de
de ![]() façons et on ajoute la boule
façons et on ajoute la boule ![]() à ces
à ces ![]() boules.
boules.
Lorsque ![]() le nombre de tirages de
le nombre de tirages de ![]() boules dont le plus grand élément est égal à
boules dont le plus grand élément est égal à ![]() est égal à
est égal à ![]()
c) Soit ![]() l’ensemble des tirages de
l’ensemble des tirages de ![]() boules parmi
boules parmi ![]() boules numérotées de
boules numérotées de ![]() à
à ![]() . On rappelle que
. On rappelle que ![]() est l’ensemble des tirages dont le plus grand numéro vaut
est l’ensemble des tirages dont le plus grand numéro vaut ![]() .
.
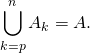 L’inclusion
L’inclusion 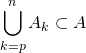 étant évidente, montrons l’inclusion réciproque. Si l’on tire
étant évidente, montrons l’inclusion réciproque. Si l’on tire ![Rendered by QuickLaTeX.com \[\mathrm{card} \left( A \right) = \displaystyle\sum_{k=p}^n \mathrm{card} \left( A_k \right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-40100e1f809e49cf128ab7ddd3a51012_l3.png)
Comme ![]() (nombres de façons de tirer
(nombres de façons de tirer ![]() boules parmi
boules parmi ![]() ) et
) et ![]() (question précédente), on a bien l’égalité souhaitée.
(question précédente), on a bien l’égalité souhaitée.
b) Se donner un tirage avec remise de ![]() boules tel que le premier numéro soit strictement inférieur au dernier revient
boules tel que le premier numéro soit strictement inférieur au dernier revient
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 :
1) a) Il ne pas y avoir de surjection car l’ensemble d’arrivée contient plus d’éléments que l’ensemble de départ. Ainsi ![]() si
si ![]()
b) Lorsque ![]() on sait que si
on sait que si ![]() est surjective, alors
est surjective, alors ![]() est injective donc
est injective donc ![]() est bijective.
est bijective.
Or, il y a ![]() bijections d’un ensemble à
bijections d’un ensemble à ![]() éléments dans un ensemble à
éléments dans un ensemble à ![]() éléments. Ainsi
éléments. Ainsi ![]()
Si ![]() il n’y a qu’une seule application : l’application qui à chaque élément de l’ensemble de départ associe l’unique élément de l’ensemble d’arrivée. Cette application étant surjective, il y a
il n’y a qu’une seule application : l’application qui à chaque élément de l’ensemble de départ associe l’unique élément de l’ensemble d’arrivée. Cette application étant surjective, il y a ![]() application et
application et ![]()
c) Rappelons qu’il y a ![]() applications d’un ensemble à
applications d’un ensemble à ![]() éléments vers un ensemble à
éléments vers un ensemble à ![]() éléments, disons
éléments, disons ![]() . Parmi toutes ces applications, seules deux ne sont pas surjectives : celle qui à tout élément de l’ensemble de départ associe l’élément
. Parmi toutes ces applications, seules deux ne sont pas surjectives : celle qui à tout élément de l’ensemble de départ associe l’élément ![]() et celle qui à tout élément de l’ensemble de départ associe l’élément
et celle qui à tout élément de l’ensemble de départ associe l’élément ![]()
d) Définir une surjection d’un ensemble ![]() à
à ![]() éléments vers un ensemble
éléments vers un ensemble ![]() à
à ![]() éléments revient :
éléments revient :
2) a) La formule
![]()
est facile à vérifier en revenant à la définition des coefficients binomiaux.
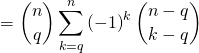
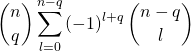
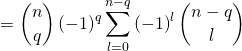
b) Il est clair que 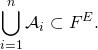
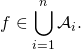
![]()
Il nous reste à calculer ![]()
![Rendered by QuickLaTeX.com \[k^p = \displaystyle\sum_{i=1}^k \displaystyle\binom{k}{i} S_i^p,\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d5870637a44760a593d7fa63050b3451_l3.png)
puis
![Rendered by QuickLaTeX.com \[\left( - 1 \right)^k \displaystyle\binom{n}{k} k^p = \displaystyle\sum_{i=1}^k \left(- 1 \right)^k \displaystyle\binom{n}{k} \displaystyle\binom{k}{i} S_i^p.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0daf6aea46dc631ae62f9adab77c4a00_l3.png)
On somme cette relation entre ![]() et
et ![]() puis on intervertit les deux sommes :
puis on intervertit les deux sommes :
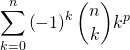
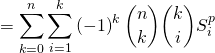
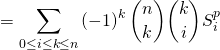
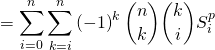
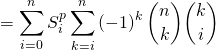 .
.
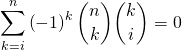 pour
pour 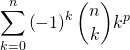
![Rendered by QuickLaTeX.com \[S_n^p = \left( - 1 \right)^n \sum_{k=0}^n \left( - 1 \right)^k \displaystyle\binom{n}{k} k^p.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8f5bfd6bce127234bf2df81abae7c3e3_l3.png)
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Lors de la correction de vos exercices, pensez à prendre note de vos erreurs et relisez régulièrement les règles ou méthodes qui vous posent problème. Faites de même pour les autres chapitres au programme d’ECG1 en Maths :

