Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés d’exercices : Séries numériques en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Séries numériques
Exercice 1 :
1) Pour tout ![]() on a
on a ![]() et que l’on sait que la série
et que l’on sait que la série ![]() converge (c’est une série exponentielle), il en résulte que la série
converge (c’est une série exponentielle), il en résulte que la série ![]() converge. Ainsi
converge. Ainsi
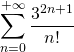
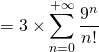
![]() .
.
2) Pour tout ![]() on a
on a ![]() et que l’on sait que la série
et que l’on sait que la série ![]() converge, il s’ensuit que la série
converge, il s’ensuit que la série ![]() converge. De plus, on a
converge. De plus, on a
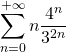
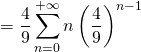
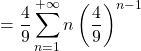
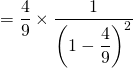
![]() .
.
3) Pour tout ![]() on a
on a ![]() Soit
Soit ![]() on a
on a
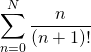
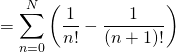
![]() .
.
![Rendered by QuickLaTeX.com \[\displaystyle\sum_{n=0}^{+ \infty} \dfrac{n}{ \left( n + 1 \right)!} = 1.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b134390d2bf51915e4aadf296e398281_l3.png)
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 :
1) La série ![]() converge si, et seulement si,
converge si, et seulement si, ![]() C’est le critère de Riemann qui l’assure !
C’est le critère de Riemann qui l’assure !
2) Soit ![]() Soit
Soit ![]() la fonction définie sur
la fonction définie sur ![]() par
par ![]()
On somme cette relation pour
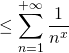
On ajoute
Ainsi, en multipliant par
Comme
![]()
Exercice 3 :
1) Pour ![]() on a
on a ![]() On en déduit que la suite
On en déduit que la suite ![]() est décroissante.
est décroissante.
![]()
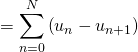
![]()
![]()
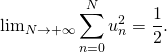 Ainsi la série
Ainsi la série 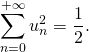
![]()
![]()
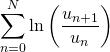
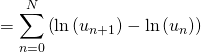
Comme
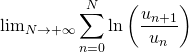
La série
4) Remarquons, que pour ![]() on a
on a ![]() ainsi
ainsi
car
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 4 :
![]() On suppose que la série
On suppose que la série ![]() converge, montrons que la série
converge, montrons que la série ![]() converge.
converge.
En sommant cette inégalité entre
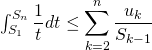
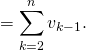
Or
![Rendered by QuickLaTeX.com \[\lim_{n \to + \infty} \displaystyle\sum_{k=2}^n v_{k - 1} = + \infty,\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7c9e9a7a38eab01a98c058563bd1bcaa_l3.png)
soit la série ![]() diverge.Si vous êtes déjà parfaitement à l’aise avec ce cours de maths en ECG1, vérifiez si vos connaissances sont aussi solides dans les autres cours :
diverge.Si vous êtes déjà parfaitement à l’aise avec ce cours de maths en ECG1, vérifiez si vos connaissances sont aussi solides dans les autres cours :