Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés : Stratégies de calcul en ECG1
Cours en ligne de Maths en ECG1
Corrigés – Stratégies de calcul
Exercice 1 :
Si l’on prouve que 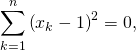 comme somme de termes positifs, on en déduit que pour tout
comme somme de termes positifs, on en déduit que pour tout ![]()
![]() soit
soit ![]()
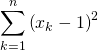 se justifie par la possibilité d’introduire les sommes données par l’énoncé :
se justifie par la possibilité d’introduire les sommes données par l’énoncé : 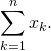
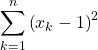
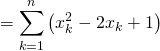
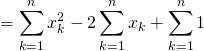
Exercice 2 :
1) Si pour tout ![]()
![]() alors les deux membres de l’inégalité sont nuls, l’inégalité est donc claire.
alors les deux membres de l’inégalité sont nuls, l’inégalité est donc claire.
2) a) Pour démontrer que ![]() est un trinôme de degré
est un trinôme de degré ![]() développons
développons ![]() :
:
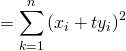
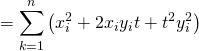
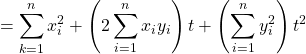 .
. b) Si ![]()
![]() s’annule en changeant de signe, ce qui contredit
s’annule en changeant de signe, ce qui contredit ![]() pour tout
pour tout ![]() donc
donc ![]()
![]()
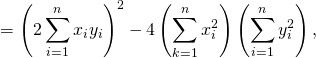
d’où
![Rendered by QuickLaTeX.com \[\left( \displaystyle\sum_{i=1}^n x_i y_i \right)^2 \le \left( \displaystyle\sum_{k=1}^n x_i^2 \right) \left( \displaystyle\sum_{i=1}^n y_i^2 \right) .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f2616a2d52ced14a454096b661a0b015_l3.png)
Et en passant à la racine carrée (attention 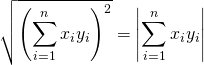 ), on a bien l’inégalité voulue.
), on a bien l’inégalité voulue.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 3 :
1) Il faut revenir à la définition de ![]() : c’est le réel qui, élevé au cube donne vaut
: c’est le réel qui, élevé au cube donne vaut ![]() On a
On a
![]()
On a aussi
![]()
On a trouvé deux nombres qui élevés au cube donnent ![]() ils sont donc égaux. Finalement
ils sont donc égaux. Finalement
![]()
2) Il suffit d’écrire ![]() et de développer.
et de développer.
3) On a :
![Rendered by QuickLaTeX.com \times \left( \underbrace { \sqrt[3]{{45 + 29 \sqrt{2}}} + \sqrt[3]{45 - 29 \sqrt{2}} }_{=S} \right)](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6ccd38b2ade8f8254025fed3ce0d0157_l3.png) .
. ![]()
4) Étudions la fonction ![]() définie par
définie par ![]() Un simple calcul donne
Un simple calcul donne ![]() Cela donne le tableau suivant :
Cela donne le tableau suivant :
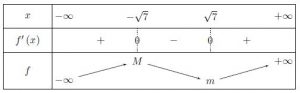
5) En testant quelques entiers naturels supérieurs à ![]() on remarque que
on remarque que ![]() Ainsi, par unicité du zéro de
Ainsi, par unicité du zéro de ![]() on a
on a ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Prenez dès à présent de l’avance sur le programme de Maths en révisant avec ces cours en ligne :


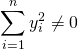 donc
donc