Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés : Suites réelles en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Suites réelles
Exercice 1 :
1) C’est faux !
En effet, prenons 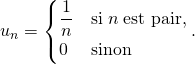 Il est clair que
Il est clair que ![]() converge vers
converge vers ![]() et qu’elle n’est pas décroissante car
et qu’elle n’est pas décroissante car ![]() pour tout
pour tout ![]()
2) C’est faux encore !
En effet, en utilisant la racine carrée, on obtient la convergence de la suite ![]() Puis
Puis ![]() donc
donc ![]() converge…
converge…
Pour trouver un contre-exemple, prenons ![]()
![]() donc la suite
donc la suite ![]() converge et pourtant
converge et pourtant ![]() diverge car les suites extraites
diverge car les suites extraites ![]() et
et ![]() convergent vers des limites différentes (
convergent vers des limites différentes (![]() et
et ![]() ).
).
3) Si l’on rajoute l’hypothèse ![]() c’est vrai ! En effet, la suite
c’est vrai ! En effet, la suite ![]() converge et
converge et ![]()
4) C’est vrai !
Si l’on appelle ![]() la limite de la suite
la limite de la suite ![]() alors en écrivant la définition de la limite, on a :
alors en écrivant la définition de la limite, on a :
![]()
![]()
En choisissant ![]() par l’inégalité triangulaire, si
par l’inégalité triangulaire, si ![]()
![]()
Puis on introduit ![]() on a, en distinguant les cas
on a, en distinguant les cas ![]() et
et ![]()
![]()
5) C’est vrai et c’est du cours !
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 :
1) La suite ![]() est définie par une somme, on calcule
est définie par une somme, on calcule
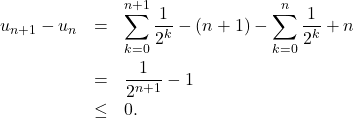
Donc la suite ![]() est décroissante.
est décroissante.
2) La suite est définie par un quotient et ![]() calculons
calculons ![]() :
:
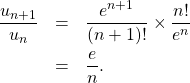
Comme ![]() on a
on a ![]() pour
pour ![]() Il s’ensuit que la suite
Il s’ensuit que la suite ![]() est décroissante.
est décroissante.
3) Si ![]() alors
alors ![]() On a pour
On a pour ![]()
![]()
![]() dès que
dès que ![]() Ainsi la suite
Ainsi la suite ![]() est décroissante.
est décroissante.
Exercice 3 :
1) On a ![]() Or
Or ![]() soit
soit ![]() donc la suite
donc la suite ![]() est croissante.
est croissante.
2) Comme la suite ![]() est bornée, la suite
est bornée, la suite ![]() l’est comme différence de deux suites bornées. La suite
l’est comme différence de deux suites bornées. La suite ![]() étant croissante et majorée converge vers une limite notée
étant croissante et majorée converge vers une limite notée ![]() On montre que
On montre que ![]()
Pour cela, on raisonne par l’absurde et on suppose, par exemple, ![]() le cas
le cas ![]() se traitant de manière analogue. On écrit que
se traitant de manière analogue. On écrit que ![]()
![]()
On a le choix de ![]() prenons
prenons ![]() de sorte que
de sorte que ![]() ainsi pour tout
ainsi pour tout ![]() on a
on a ![]()
Soit ![]() en sommant la relation précédente pour
en sommant la relation précédente pour ![]() compris entre
compris entre ![]() et
et ![]() on obtient :
on obtient : 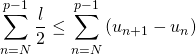 soit
soit ![]() puis
puis ![]()
Par minoration par une suite qui diverge vers ![]()
![]() Cela contredit le fait que la suite
Cela contredit le fait que la suite ![]() est bornée. Ainsi
est bornée. Ainsi ![]()
Exercice 4 :
1) La suite ![]() est une suite récurrente linéaire d’ordre
est une suite récurrente linéaire d’ordre ![]() La méthode est classique. L’équation caractéristique est
La méthode est classique. L’équation caractéristique est ![]() On a
On a ![]() Ainsi, l’équation caractéristique a deux solutions réelles :
Ainsi, l’équation caractéristique a deux solutions réelles : ![]() et
et ![]()
Ainsi, il existe deux constantes réelles ![]() et
et ![]() telles que : pour tout
telles que : pour tout ![]()
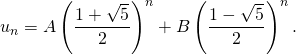
Pour trouver ![]() et
et ![]() utilisons les valeurs de
utilisons les valeurs de ![]() et
et ![]() Cela donne le système suivant :
Cela donne le système suivant :
![Rendered by QuickLaTeX.com \[\begin{cases} A + B & = 0 \\ A \dfrac{1 + \sqrt{5}}{2} + B \dfrac{1 - \sqrt{5}}{2} & = 1 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7ec4087a3bd9ba6c9824a5a500b564c9_l3.png)
La résolution de ce système donne ![]() et
et ![]() Si bien que pour tout
Si bien que pour tout ![]()
![Rendered by QuickLaTeX.com \[u_n = \dfrac{1}{\sqrt{5}} \left( \dfrac{1 + \sqrt{5}}{2} \right)^n - \dfrac{1}{\sqrt{5}} \left( \dfrac{1 - \sqrt{5}}{2} \right)^n .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-716ec889815210619003f1dd1ee983c7_l3.png)
2) La suite ![]() est arithmético-géométrique.
est arithmético-géométrique.
On résout l’équation ![]() Cela donne
Cela donne ![]()
Soit la suite ![]() définie par
définie par ![]() Il est facile de voir que
Il est facile de voir que ![]() est géométrique de raison
est géométrique de raison ![]()
Ainsi pour tout ![]() on a
on a ![]()
D’où ![]() et
et ![]()
3) Il est facile de montrer, par récurrence double (faites-la !) que, pour tout ![]() on a
on a ![]() Posons
Posons ![]() La suite
La suite ![]() vérifie :
vérifie :
![]()
![]() est une suite récurrente linéaire d’ordre
est une suite récurrente linéaire d’ordre ![]() \`a coefficients constants. L’équation caractéristique est
\`a coefficients constants. L’équation caractéristique est ![]() soit
soit ![]()
![]() il y a donc deux solutions
il y a donc deux solutions ![]() et
et ![]()
Ainsi, il existe deux constantes ![]() telles que
telles que
![]()
Pour trouver ![]() et
et ![]() utilisons les valeurs de
utilisons les valeurs de ![]() et
et ![]() Cela donne le système :
Cela donne le système :
![Rendered by QuickLaTeX.com \[\begin{cases} A + B & = 0 \\ A - \dfrac12 B & = 1 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-827fa4bc2f15a1c3f5f264a8cc2cba4e_l3.png)
La résolution de ce système donne ![]() et
et ![]() Ainsi pour tout
Ainsi pour tout ![]()
![]() puis
puis
![]()
4) Cherchons une suite « simple » vérifiant la relation ![]() On la cherche sous la forme
On la cherche sous la forme ![]() avec
avec ![]() En substituant
En substituant ![]() dans la relation, on a :
dans la relation, on a : ![]() soit
soit ![]() En identifiant les termes devant
En identifiant les termes devant ![]() et les termes constants, on obtient le système :
et les termes constants, on obtient le système :
![Rendered by QuickLaTeX.com \[\begin{cases} a & = 2 a + 1 \\ a + b & = 2 b + 3 \end{cases},\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-272b7040c92150a0662ebe826371b5b7_l3.png)
soit ![]() et
et ![]()
Soit la suite ![]() définie par
définie par ![]()
Il est facile de voir que ![]() est géométrique de raison
est géométrique de raison ![]() d’o\`u pour tout
d’o\`u pour tout ![]()
![]() Or
Or ![]() et
et ![]() et
et
![]()
5) La relation donnée est équivalente à ![]()
En posant ![]() la relation précédente montre que la suite
la relation précédente montre que la suite ![]() est constante. Ainsi pour tout
est constante. Ainsi pour tout ![]()
![]()
On a donc montré que pour tout ![]()
![]() avec
avec ![]() La suite
La suite ![]() est donc arithmético-géométrique.
est donc arithmético-géométrique.
La suite est classique : on pose ![]() La suite
La suite ![]() est géométrique de raison
est géométrique de raison ![]() ainsi pour tout
ainsi pour tout ![]() on a
on a ![]() Or
Or ![]() d’où, pour tout
d’où, pour tout ![]()
![]() pour tout
pour tout ![]() et donc
et donc ![]() pour tout
pour tout ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Si certaines difficultés persistent, n’hésitez pas à télécharger l’application gratuite PrepApp sur laquelle de nombreux autres exercices et corrigés sont disponibles. Sinon, vous pouvez aussi consulter d’autres cours de maths d’ECG1 :

