Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés : Variables aléatoires discrètes en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Variables aléatoires discrètes
Exercice :
1) ![]() suit une loi binomiale
suit une loi binomiale ![]() En effet,
En effet, ![]() compte le nombre de transmissions de messages contraires qui est une répétition de
compte le nombre de transmissions de messages contraires qui est une répétition de ![]() d’épreuves indépendantes ayant
d’épreuves indépendantes ayant ![]() issues possibles : le message transmis est le contraire du message précédent avec une probabilité
issues possibles : le message transmis est le contraire du message précédent avec une probabilité ![]() et coïncide avec le message reçu avec une probabilité
et coïncide avec le message reçu avec une probabilité ![]()
2) a) Comme la variable aléatoire ![]() est à valeurs entières, si
est à valeurs entières, si ![]()
![]() est un entier naturel pair ou impair donc, on a
est un entier naturel pair ou impair donc, on a ![]() Ainsi
Ainsi
![]()
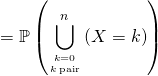
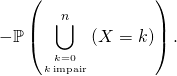
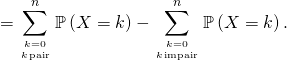
Cela donne les calculs suivants :
![Rendered by QuickLaTeX.com = \displaystyle\sum_{k \in [\![ 0, n ]\!] \atop k \; \text{pair}} \binom{n}{k} q^{k} p^{n - k}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e10f5d05a43de27f0e72245c2711e541_l3.png)
![Rendered by QuickLaTeX.com - \displaystyle\sum_{k \in [\![ 0, n ]\!] \atop k \; \text{impair}} \binom{n}{k} q^k p^{n - k}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d55f63b412962052ba1a36cf1112a1cc_l3.png)
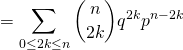
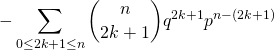
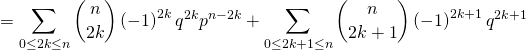
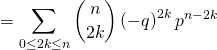
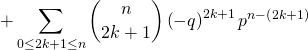
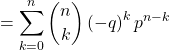
c) On reconnaît la formule du binôme de Newton dans cette dernière expression, ainsi ![]()
![]() Or
Or ![]() donc
donc
Pour calculer
![Rendered by QuickLaTeX.com \[\begin{cases} \mathbb{P} \left( E \right) + \mathbb{P} \left( F \right) & = 1 \\ \mathbb{P} \left( E \right) - \mathbb{P} \left( F \right) & = \left( 1 - 2 q \right)^n \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-de82f21c1a46a948da56f0d4c8422951_l3.png)
La résolution de ce système donne ![]()
![]()
4) Comme ![]() on a :
on a : ![]() donc
donc ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Retrouvez gratuitement les autres chapitres importants au programme de maths en ECG1, tels que :

