Chapitres Maths en ECG1

Corrigés : Variables aléatoires finies en ECG1

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices Corrigés

Cours en ligne de Maths en ECG1

Corrigés – Variables aléatoires finies

Exercice 1 :

1) Pour réaliser $\left( X = 2 \right),$ on doit avoir $P_1 F_2.$ Ainsi $\mathbb{P} \left( X = 2 \right) = \mathbb{P} \left( P_1 F_2 \right).$ Par indépendance des événements, on a $\mathbb{P} \left( P_1 F_2 \right)$ $= \mathbb{P} \left( P_1 \right) \times \mathbb{P} \left( F_2 \right)$ $= \dfrac14.$ Ainsi

$\mathbb{P} \left( X = 2 \right) = \dfrac14.$

2) a) Les deux derniers tirages sont $P_2 F_3.$ Le premier tirage pouvant être Pile ou Face, on a bien

$\left( X= 3 \right) = P_1 P_2 F_3 \cup F_1 P_2 F_3.$

Ainsi

$\mathbb{P} \left( X= 3 \right)$

$= \mathbb{P} \left( P_1 P_2 F_3 \cup F_1 P_2 F_3 \right)$

$\text{les evenements etant disjoints}$

$= \mathbb{P} \left( P_1 P_2 F_3 \right) + \mathbb{P} \left( F_1 P_2 F_3 \right)$

$\text{par independance}$

$=\mathbb{P} \left( P_1 \right) \times \mathbb{P} \left( P_2 \right) \times \mathbb{P} \left( F_3 \right)$

$+ \mathbb{P} \left( F_1 \right) \times \mathbb{P} \left( P_2 \right) \times \mathbb{P} \left( F_3 \right)$

$= \dfrac18 + \dfrac18$

$= \dfrac14$ .

b) Les deux derniers lancers sont

$P_{k - 1} F_k.$ On s’intéresse aux

$k - 2$ premiers lancers. Deux possibilités :

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

$\star$ il n’y a pas de Pile lors des

$k - 2$ premiers lancers, auquel cas, le lancer est de la forme

$F_1 F_2 \cdots F_{k - 2} P_{k - 1} F_k.$

$\star$ il y a au moins un Pile lors des

$k - 2$ premiers lancers. On appelle par

$k- 2 \ge j \ge 1$ le rang d’apparition du premier Pile. Ainsi, les

$j - 1$ premiers lancers sont Face. Remarquons que les lancers obtenus aux rangs

$j + 1, j + 2, \cdots , k- 2$ sont Pile.

En effet, si l’on avait un Face au cours de ces lancers. En notant

$l$ le rang d’apparition du premier Face au cours de ces lancers, on aurait un lancer du type

$F_1 \cdots F_{j - 1} P_j P_{j + 1} \cdots P_{l - 1} F_l \cdots P_{k - 1} F_k.$

Ainsi le rang d’apparition du premier groupement Pile puis Face serait en position

$l < k,$ ce qui n’est possible puisque l’on travaille sur l’événement

$\left( X = k \right).$ Finalement, le lancer est de la forme

$F_1 F_2 \cdots F_{j - 1} P_j P_{j + 1} \cdots P_{k - 1} F_k.$

On a bien

$\left( X= k \right)$

$= \left( F_1 F_2 \cdots F_{k - 2} P_{k - 1} F_k \right)$

$\cup (\displaystyle\bigcup_{j=1}^{k - 2} \left( F_1 \cdots F_{j - 1} P_j P_{j + 1} \cdots P_{k - 1} F_k \right) ).$
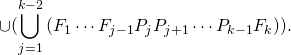
Notons que ces

$k - 1$ événements sont deux à deux disjoints.

c) A la question précédente, nous avons écrit

$\left( X = k \right)$ comme réunion de

$k - 1$ événements deux à deux disjoints. Remarquons que, par indépendance des lancers, chacun de ces événements est de probabilité égale à

$\left( \dfrac12 \right)^k.$ Les événements étant disjoints, on a:

$\mathbb{P} \left( X = k \right)$

$= \left( k - 1 \right) \left( \dfrac12 \right)^k.$

d) Remarquons que

$X \left( \Omega \right) = \mathbb{N} \backslash \left\{ 1 \right\}.$ Ainsi

$\mathbb{P} \left( X = 0 \right)$ $= 1 - \mathbb{P} \left( X \ge 2 \right)$
$= 1 - \displaystyle\sum_{k=2}^{+ \infty} \left( k - 1 \right) \left( \dfrac12 \right)^k$
$\underset{\text{on pose} \; l = k - 1}{=} 1 - \displaystyle\sum_{l=1}^{+ \infty} l \left( \dfrac12 \right)^{l + 1}$
$= 1 - \dfrac14 \displaystyle\sum_{l=1}^{+ \infty} l \left( \dfrac12 \right)^{l - 1}$
$= 1 - \dfrac14 \times \dfrac{1}{\left( 1 - \dfrac12 \right)^2}$
$= 0$ .

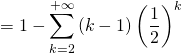
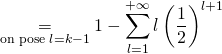
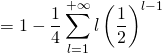
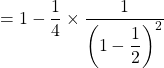
3) a) On suppose que le premier lancer est Pile.

$\bullet$ Si

$P_2 P_3 \cdots P_{k- 1} F_k$ se réalise. Comme le premier lancer est Pile,

$P_1 P_2 \cdots P_{k - 1} F_k$ se réalise. Ainsi,

$\left( X = k \right)$ se réalise car le premier groupement Pile puis Face est en position

$k-1$ et

$k.$

$\bullet$ Réciproquement, supposons que

$\left( X = k \right)$ se réalise. Montrons qu’il n’y a pas de Face lors dans lancers de rang

$2, 3 , \cdots, k - 2.$ S’il y en a un, on note par

$j < k$ le rang d’apparition du premier Face. Ainsi, on a

$P_1 P_2 \cdots P_{j - 1} F_j.$

Ici, on remarque que le rang d’apparition du premier groupement Pile puis Face est au rang

$j,$ ce qui est impossible car l’on travaille avec l’événement

$\left( X = k \right).$

b) Le famille

$\left\{ P_1 , F_1 \right\}$ est un système complet d’événements. la formule des probabilités totales assure que

$\mathbb{P} \left( X = k \right)$

$= \mathbb{P}_{P_1} \left( X = k \right) \times \mathbb{P} \left( P_1 \right)$

$+ \mathbb{P}_{F_1} \left( X = k \right) \times \mathbb{P} \left( F_1 \right).$

Or, à la question précédente, on a montré que

$\mathbb{P}_{P_1} \left( X = k \right)$

$= \mathbb{P} \left( P_2 P_3 \cdots P_{k - 1} F_k \right)$

$= \dfrac{1}{2^{k - 1}}.$ remarquons aussi que lévénement

$\left( X = k \right)$ sachant

$F_1$ est équivalent à

$\left( X = k - 1 \right),$ ainsi

$\mathbb{P} \left( X = k \right)$

$= \dfrac{1}{2^{k - 1}} \times \mathbb{P} \left( P_1 \right)$

$+ \mathbb{P} \left( X = k - 1 \right) \times \mathbb{P} \left( F_1 \right)$

$= \dfrac{1}{2^k} + \dfrac12 \mathbb{P} \left( X = k - 1 \right)$ .

c) En multipliant la relation obtenue à la question précédente, on a:

$2^k \mathbb{P} \left( X = k \right)$

$= 2^{k - 1} \mathbb{P} \left( X = k - 1 \right) + 1,$
soit

$u_k = u_{k - 1} + 1.$

La suite

$\left( u_k \right)_{k \ge 2}$ est arithmétique de raison

$1.$ Pour tout

$k \ge 2,$ on a

$u_k = u_2 + \left( k - 2 \right) r,$

d’où

$u_k = k -1$ et

$\mathbb{P} \left( X = k \right)$

$= \dfrac{k - 1}{2^k}.$

d) En multipliant la relation obtenue à la question précédente, on a:

$2^k \mathbb{P} \left( X = k \right)$

$= 2^{k - 1} \mathbb{P} \left( X = k - 1 \right) + 1,$
soit

$u_k = u_{k - 1} + 1.$

La suite

$\left( u_k \right)_{k \ge 2}$ est arithmétique de raison

$1.$ Pour tout

$k \ge 2,$ on a

$u_k = u_2 + \left( k - 2 \right) r,$

d’où

$u_k = k -1$ et

$\mathbb{P} \left( X = k \right)$

$= \dfrac{k - 1}{2^k}.$

4) Pour montrer que

$X$ admet une espérance, montrons que la série

$\displaystyle\sum_{k \ge 2} k \mathbb{P} \left( X = k \right)$ converge absolument.

Par croissance comparée, on a

$\lim_{k \to + \infty} k^2 \times \dfrac{k - 1}{2^k} = 0.$

Ainsi

$\dfrac{k -1}{2^{k - 1}} \underset{k \to + \infty}{=} o \left( \dfrac{1}{k^2} \right).$ Comme la série de terme général

$\displaystyle\sum_{k \ge 2} \dfrac{1}{k^2}$ converge (Riemann), la série

$\displaystyle\sum_{k \ge 2} k \mathbb{P} \left( X = k \right)$ converge et

$X$ admet une espérance et

$\mathbb{E} \left( X \right)$

$= \displaystyle\sum_{k=2}^{+ \infty} k \times \dfrac{k - 1}{2^k}$

$= \left( \dfrac12 \right)^2 \displaystyle\sum_{k=2}^{+ \infty} k \left( k - 1 \right) \left( \dfrac12 \right)^{k - 2}$

$= \dfrac14 \times \dfrac{2}{\left( 1 - \dfrac12 \right)^3}$

$= 4$ .

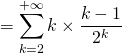
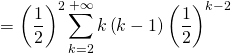
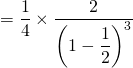
COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Pour maximiser vos résultats en ECG1, servez-vous, en plus des cours et exercices fournis en cours, de nos cours en ligne et de leurs exercices corrigés de maths en ECG1 :

Corrigés : Variables aléatoires finies en ECG1

Corrigés – Variables aléatoires finies

Exercice 1 :

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales