Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Espace probabilisé et nouveaux résultats en ECG1
Cours en ligne de Maths en ECG1
Résumé de cours et méthodes – Espace probabilisé et nouveaux résultats
Méthode 1 : Montrer qu’un ensemble est un événement.
L’ensemble des événements sur l’univers ![]() est une tribu notée
est une tribu notée ![]() (c’est une partie de
(c’est une partie de ![]() contenant
contenant ![]() stable par complémentaire et par réunion finie et dénombrable, donc par intersection finie et dénombrable).
stable par complémentaire et par réunion finie et dénombrable, donc par intersection finie et dénombrable).
Pour montrer qu’un ensemble est un événement, il suffit de réussir à l’écrire comme une réunion/intersection/complémentaire d’événements i.e. d’éléments de ![]() en considérant si nécessaire des réunions ou intersections dénombrables d’éléments de
en considérant si nécessaire des réunions ou intersections dénombrables d’éléments de ![]()
Dans le cas où ![]() est fini ou dénombrable, on choisit
est fini ou dénombrable, on choisit ![]()
![]()
Cette méthode est délicate, et rarement posée en pratique, ce qui ne vous dispense pas de savoir écrire correctement les événements étudiés en fonction d’événements plus simples. Si vous souhaitez maitriser les méthodes sur l’espace probabilisé nos profs particuliers de maths peuvent vous aider.
Exemple : On lance une infinité de fois une pièce avec un côté Pile et un côté Face.
1) Décrire ![]()
Pour tout ![]() on pose
on pose ![]() : « obtenir Pile au
: « obtenir Pile au ![]() -ième lancer » et
-ième lancer » et ![]() : « obtenir Face au
: « obtenir Face au ![]() -ième lancer ».
-ième lancer ».
On suppose qu’il existe une tribu ![]() sur
sur ![]() telle que pour tout
telle que pour tout ![]()
![]() est un événement.
est un événement.
2) Soit ![]() l’ensemble des lancers donnant une infinité de Piles et une infinité de Faces. Montrer que
l’ensemble des lancers donnant une infinité de Piles et une infinité de Faces. Montrer que ![]() est un événement.
est un événement.
Réponse :
1) ![]() est l’ensemble des possibilités.
est l’ensemble des possibilités.
2) On écrit ![]() avec
avec ![]() (resp. C) « obtenir une infinité de Piles (resp. de Faces) ».
(resp. C) « obtenir une infinité de Piles (resp. de Faces) ».
On commence par traduire ![]() :
:
![]() est réalisé si, et seulement si, pour tout
est réalisé si, et seulement si, pour tout ![]() il existe
il existe ![]() tel qu’il y ait un Pile au rang
tel qu’il y ait un Pile au rang ![]() ce qui revient à dire que pour tout
ce qui revient à dire que pour tout ![]() il existe
il existe ![]() tel que
tel que ![]() soit réalisé soit pour tout
soit réalisé soit pour tout ![]()
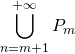 est réalisé.
est réalisé.
Donc 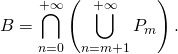
Pour tout ![]()
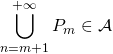 (réunion dénombrable d’éléments de
(réunion dénombrable d’éléments de ![]() ), puis comme intersection dénombrable d’éléments de
), puis comme intersection dénombrable d’éléments de ![]()
![]()
Par symétrie, 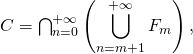 et on démontre que
et on démontre que ![]()
Finalement ![]() comme intersection de deux éléments de
comme intersection de deux éléments de ![]()
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 2 : Savoir utiliser les relations fondamentales de probabilité.
On suppose que ![]() est un espace probabilisé.
est un espace probabilisé.
Mais on a les propriétés supplémentaires :
![]() si pour tout
si pour tout ![]()
![]() et si
et si ![]() pour
pour ![]() alors
alors ![]()
![]()
![]() pour une suite croissante d’événements : si pour tout
pour une suite croissante d’événements : si pour tout ![]()
![]() et
et ![]()
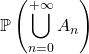
![]()
![]() pour une suite décroissante d’événements : si pour tout
pour une suite décroissante d’événements : si pour tout ![]()
![]() et
et ![]()
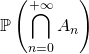
![]()
On définit encore l’indépendance de ![]() de
de ![]() événements que l’on complète par la notion de suite d’événements indépendants :
événements que l’on complète par la notion de suite d’événements indépendants :
La suite ![]() est une suite d’événements indépendants si, et seulement si, pour tout
est une suite d’événements indépendants si, et seulement si, pour tout ![]() les événements
les événements ![]() sont mutuellement indépendants.
sont mutuellement indépendants.
Exemple : On lance une infinité de fois une pièce donnant Pile avec la probabilité ![]() et Face avec la probabilité
et Face avec la probabilité ![]()
On note ![]() : « obtenir Pile au
: « obtenir Pile au ![]() -ième lancer » et
-ième lancer » et ![]() : « obtenir Face au
: « obtenir Face au ![]() -ième lancer ».
-ième lancer ».
On admet l’existence d’un espace probabilisé ![]() associé à cette épreuve pour lequel pour tout
associé à cette épreuve pour lequel pour tout ![]()
![]() est un événement, la suite
est un événement, la suite ![]() étant une suite d’événements indépendants.
étant une suite d’événements indépendants.
1) Quelle est la probabilité d’obtenir une suite de faces suivie de deux Piles ?
2) Déterminer le probabilité de l’événement « les ![]() premiers jets ont donné
premiers jets ont donné ![]() Faces » si
Faces » si ![]() Quelle est la probabilité de n’obtenir aucun Pile ?
Quelle est la probabilité de n’obtenir aucun Pile ?
Réponse : 1) On rappelle que ![]() est le complémentaire de
est le complémentaire de ![]() donc
donc ![]()
Soit si ![]()
![]() l’événement « on obtient
l’événement « on obtient ![]() Faces suivies de
Faces suivies de ![]() Piles », alors
Piles », alors ![]() Ainsi
Ainsi ![]() : « obtenir une suite de Faces se terminant par deux Piles » s’écrit
: « obtenir une suite de Faces se terminant par deux Piles » s’écrit 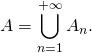
Les événements ![]() étant indépendants :
étant indépendants :
![]()
![]()
![]()
![]()
![]()
![]()
Les événements ![]() sont deux à deux incompatibles,
sont deux à deux incompatibles,
![]()
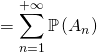
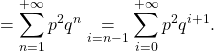
Ainsi ![]()
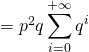
![]()
![]()
2) On note ![]() l’événement : « les
l’événement : « les ![]() premiers jets ont donné
premiers jets ont donné ![]() Faces », ainsi
Faces », ainsi ![]() ; comme ci-dessus,
; comme ci-dessus,
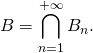
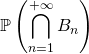
Méthode 3 : Lorsque ![]() est dénombrable, caractériser une probabilité sur
est dénombrable, caractériser une probabilité sur ![]() .
.
Dans la suite ![]()
Une probabilité sur ![]() est une application
est une application ![]() définie sur
définie sur ![]() à valeurs dans
à valeurs dans ![]() telle que :
telle que :
![]()
![]()
![]()
![]() est
est ![]() -additive : pour toute suite d’événements
-additive : pour toute suite d’événements ![]() deux à deux incompatibles, on a :
deux à deux incompatibles, on a :
![]()
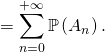
En particulier, la série de terme général ![]() converge et
converge et 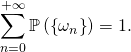
Dans ce cas pour tout ![]()
![]()
![]()
Exemple : On admet que 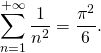
1) Montrer qu’il existe ![]() tel que l’application
tel que l’application ![]() définie sur
définie sur ![]() par : pour tout
par : pour tout ![]()
![]()
![]() est une probabilité sur
est une probabilité sur ![]()
2) On note ![]() l’ensemble des entiers pairs, donner
l’ensemble des entiers pairs, donner ![]()
Réponse :
1) Pour tout ![]()
![]() si et seulement si
si et seulement si ![]() La série de terme général
La série de terme général ![]() converge par comparaison par équivalence avec une série de Riemann convergente. Or
converge par comparaison par équivalence avec une série de Riemann convergente. Or
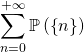
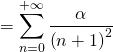
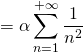
Finalement
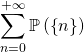
On a montré que
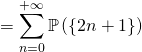
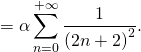 Si l’on pose
Si l’on pose 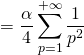
On suppose que ![]() est un espace probabilisé.
est un espace probabilisé.
On dit que ![]() est un événement presque impossible lorsque
est un événement presque impossible lorsque ![]() et presque certain lorsque
et presque certain lorsque ![]()
1) Probabilité conditionnelle :
si ![]() n’est pas un événement presque impossible (i.e.
n’est pas un événement presque impossible (i.e. ![]() ), on définit
), on définit ![]()
![]()
Cette formule sert aussi sous la forme ![]()
![]()
![]()
On retiendra que 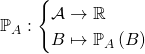 définit une probabilité sur
définit une probabilité sur ![]()
2) La formule des probabilités composées est la même.
3) Formule des probabilités totales avec un système complet d’événements dénombrable (elle reste bien sûr valable pour un système complet fini) ou un système quasi-complet d’événements (elle reste bien sûr valable pour un système complet fini) :
On suppose que l’on a une suite d’événements deux à deux incompatibles tels que 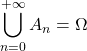 (système complet d’événements) ou
(système complet d’événements) ou ![]() est quasi-certain (système quasi-complet d’événements), pour tout
est quasi-certain (système quasi-complet d’événements), pour tout ![]()
![]()
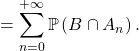
De plus, si pour tout ![]()
![]() on peut écrire :
on peut écrire :
![]()
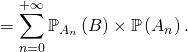
4) Formule de Bayès, avec les hypothèses développées au point 3), on peut écrire lorsque ![]()
![]()
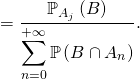
D’autres cours en ligne de mathématiques au programme d’ECG1 sont également accessibles, dont :

