Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Espaces vectoriels & Applications Linéaires
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Résumé de cours, méthodes – Espaces vectoriels/applications linéaires
1. Premières notions sur les espaces vectoriels et les familles de vecteurs
Méthode 1 : Montrer qu’un ensemble est un espace vectoriel.
Pour montrer qu’un ensemble est un espace vectoriel, on montre que c’est un sous espace vectoriel d’un espace vectoriel de référence.
On rappelle quelques espaces vectoriels de référence :
![]() (
(![]() -uplets),
-uplets),
![]() (polynômes réels),
(polynômes réels),
![]() (polynômes réels de degré inférieur à
(polynômes réels de degré inférieur à ![]() ),
),
![]() (matrices réelles de taille
(matrices réelles de taille ![]() ),
),
![]() (fonctions réelles de classe
(fonctions réelles de classe ![]() sur un intervalle
sur un intervalle ![]() ),
),
![]() (ensemble des suites réelles), etc.
(ensemble des suites réelles), etc.
On rappelle que pour montrer qu’un ensemble ![]() est un sous espace vectoriel de
est un sous espace vectoriel de ![]() , on montre qu’il est non vide (on montre que
, on montre qu’il est non vide (on montre que ![]() est dans
est dans ![]() ) et que pour tout
) et que pour tout ![]() pour tout
pour tout ![]()
![]()
Exemple :Montrer que les espaces suivants sont des espaces vectoriels :
![]()
Réponse :
Clairement ![]()
Soit ![]() et soit
et soit ![]() Montrons que
Montrons que
![]()
![]()
Pour voir cela, écrivons :
![]()
![]()
On rappelle que si ![]() sont des vecteurs d’un
sont des vecteurs d’un ![]() -espace vectoriel
-espace vectoriel ![]() on appelle
on appelle ![]() le sous espace vectoriel formé par toutes les combinaisons linéaires des vecteurs
le sous espace vectoriel formé par toutes les combinaisons linéaires des vecteurs ![]() :
:
![]()
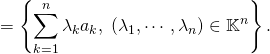
En conséquence si l’on reconnaît dans une partie de ![]() de l’espace vectoriel
de l’espace vectoriel ![]() une écriture de la forme
une écriture de la forme 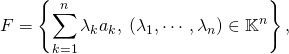 on peut conclure que
on peut conclure que ![]() donc
donc ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]()
Exemple : Montrer que l’ensemble suivant est un espace vectoriel :
![]()
Réponse : On remarque que
![]() si, et seulement si,
si, et seulement si, ![]()
Donc ![]() avec
avec ![]()
Si bien que ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]()
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 3 : Montrer qu’une famille est une famille libre dans un ![]() -espace vectoriel.
-espace vectoriel.
Voici quelques méthodes que l’on peut essayer, la méthode ![]() étant la plus importante :
étant la plus importante :
![]() La famille
La famille ![]() est libre si, et seulement si,
est libre si, et seulement si, ![]()
![]() Pour démontrer que la famille
Pour démontrer que la famille ![]() est libre, il est en général plus simple de prouver que
est libre, il est en général plus simple de prouver que ![]() et que la condition
et que la condition ![]() où
où ![]() est impossible.
est impossible.
![]() Pour montrer qu’une famille de vecteurs
Pour montrer qu’une famille de vecteurs ![]() est libre, on revient généralement à la définition, c’est-à-dire que l’on se donne
est libre, on revient généralement à la définition, c’est-à-dire que l’on se donne ![]() tels que
tels que
![]()
et on montre que ![]()
![]() Si l’on sait que la famille
Si l’on sait que la famille ![]() est libre, pour démontrer que la famille
est libre, pour démontrer que la famille ![]() est libre, il suffit de montrer que la relation
est libre, il suffit de montrer que la relation
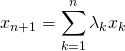 où
où ![]() est impossible.
est impossible.
Voici, en vrac, quelques idées qui peuvent aussi servir à montrer qu’une famille est libre :
![]() Une famille de polynômes de degrés échelonnés (c’est-à-dire de degrés entiers deux à deux distincts, donc ne contenant pas le polynôme nul) est libre.
Une famille de polynômes de degrés échelonnés (c’est-à-dire de degrés entiers deux à deux distincts, donc ne contenant pas le polynôme nul) est libre.
![]() Lorsque l’on doit montrer qu’une famille de fonctions est libre, il peut être utile de prendre des valeurs de
Lorsque l’on doit montrer qu’une famille de fonctions est libre, il peut être utile de prendre des valeurs de ![]() bien choisies.
bien choisies.
![]() Toujours avec des fonctions, il peut être parfois intéressant d’utiliser des propriétés d’analyse (continuité, dérivabilité, etc).
Toujours avec des fonctions, il peut être parfois intéressant d’utiliser des propriétés d’analyse (continuité, dérivabilité, etc).
Exemple : Montrer que ![]() est libre dans
est libre dans ![]()
Réponse :
On pourrait prendre des valeurs particulières pour ![]() mais on va procéder autrement. On se donne trois réels
mais on va procéder autrement. On se donne trois réels ![]() et
et ![]() tels que
tels que ![]() montrons que
montrons que ![]()
![]() Pour montrer qu’une famille de vecteurs
Pour montrer qu’une famille de vecteurs ![]() de
de ![]() est génératrice de
est génératrice de ![]() , on montre que
, on montre que ![]() En pratique, pour tout
En pratique, pour tout ![]() on cherche des scalaires
on cherche des scalaires ![]() tels que
tels que 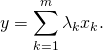
![]() Dans le cas où l’on sait que
Dans le cas où l’on sait que ![]() pour démontrer qu’une famille de vecteurs
pour démontrer qu’une famille de vecteurs ![]() de
de ![]() est génératrice de
est génératrice de ![]() il suffit de prouver que pour tout
il suffit de prouver que pour tout ![]()
![]() est combinaison linéaire de vecteurs de
est combinaison linéaire de vecteurs de ![]()
Exemple : On se place dans ![]()
On note ![]() avec
avec ![]() et
et ![]() On note
On note ![]() et
et ![]() Montrer que
Montrer que ![]() est un système générateur de
est un système générateur de ![]()
Réponse : On pose ![]()
![]() De simples calculs montrent que
De simples calculs montrent que ![]() et
et ![]() les vecteurs
les vecteurs ![]() et
et ![]() qui engendrent
qui engendrent ![]() sont combinaisons linéaires de vecteurs de
sont combinaisons linéaires de vecteurs de ![]() donc
donc ![]()
![]() On cherche des réels
On cherche des réels ![]() tels que
tels que ![]() On obtient le système :
On obtient le système :
![Rendered by QuickLaTeX.com \[\begin{cases} \alpha + \beta + \gamma & = 1 \\ \alpha - \beta - \gamma & = 0 \\- \alpha + \beta - \gamma & = 0 \\ - \alpha - \beta + \gamma & = - 1 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-097d61e688ffee58efac668f72e690c9_l3.png)
En formant ![]()
![]() et
et ![]() on obtient
on obtient
![Rendered by QuickLaTeX.com \[\begin{cases} \alpha + \beta + \gamma & = 1 \\ 2 \alpha & = 1 \\ 2 \beta & = 1 \\ 2 \gamma & = 0 \end{cases},\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4344c0790ea7b31f3e35b1b2bc5b1d18_l3.png)
alors ![]()
2. Espaces vectoriels de dimension finie
Méthode 5 : Montrer qu’une famille est une base.
On rappelle qu’une base est une famille libre et génératrice. En général, vous devrez justifier ces deux propriétés successivement. Je ne peux que vous conseiller de revoir les définitions et les méthodes du précédentes !
Remarque : Il est indispensable de noter les bases sous forme de listes, puisque l’ordre des éléments d’une base est important pour écrire les coordonnées des vecteurs.
Exemple : Soit ![]()
1) Montrer que ![]() est un espace vectoriel.
est un espace vectoriel.
2) Donner une base de ![]()
Réponse :
1) La méthode est classique. ![]() est une partie non vide (car contenant le polynôme nul) de l’espace vectoriel
est une partie non vide (car contenant le polynôme nul) de l’espace vectoriel ![]() On se donne
On se donne ![]() et
et ![]() Montrons que
Montrons que ![]() Pour cela, on montre que
Pour cela, on montre que ![]() En effet,
En effet,
![]()
![]()
![]() .
.
Ainsi, ![]() est un sous espace vectoriel de
est un sous espace vectoriel de ![]() donc c’est un espace vectoriel.
donc c’est un espace vectoriel.
2) Soit ![]() On écrit
On écrit ![]() et on cherche des conditions nécessaires et suffisantes sur
et on cherche des conditions nécessaires et suffisantes sur ![]() et
et ![]() pour que
pour que ![]() On écrit donc :
On écrit donc :
![]()
Ainsi ![]() La famille
La famille ![]() étant libre car c’est une famille de polynômes ayant des degrés échelonnés, la famille
étant libre car c’est une famille de polynômes ayant des degrés échelonnés, la famille ![]() est une base de
est une base de ![]() car c’est une partie libre et génératrice de
car c’est une partie libre et génératrice de ![]()
Méthode 6 : Calculer la dimension d’un espace vectoriel.
On rappelle qu’un espace vectoriel de dimension finie est, par définition, un espace vectoriel ayant une famille génératrice finie. On peut montrer (c’est dans votre cours) qu’un tel espace non réduit à ![]() admet des bases ayant un nombre fini d’éléments et que ces bases ont toutes le même nombre d’éléments.
admet des bases ayant un nombre fini d’éléments et que ces bases ont toutes le même nombre d’éléments.
En pratique, lorsque l’on demande de calculer la dimension d’un espace vectoriel, on essaie d’en trouver une base et on compte le nombre d’éléments de cette base.
Cas particuliers à connaître parfaitement :
![]() Si
Si ![]() De plus, la famille
De plus, la famille ![]() avec
avec ![]() (le
(le ![]() étant en
étant en ![]() -ème position) est une base de
-ème position) est une base de ![]() appelée base canonique.
appelée base canonique.
![]() Si
Si ![]() et la famille
et la famille ![]() est une base de
est une base de ![]() appelée base canonique.
appelée base canonique.
![]() Si
Si ![]()
Exemple : Montrer que l’ensemble suivant est un espace vectoriel et calculer sa dimension :
![]()
![]()
Réponse :
![]() est non vide car il contient le polynôme nul.
est non vide car il contient le polynôme nul.
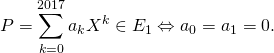
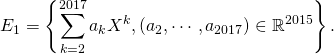
Lorsque ![]() est un espace vectoriel de dimension finie
est un espace vectoriel de dimension finie ![]() , pour montrer qu’une famille
, pour montrer qu’une famille ![]() de
de ![]() est une base, il suffit de montrer qu’elle est libre et qu’elle contient
est une base, il suffit de montrer qu’elle est libre et qu’elle contient ![]() éléments (le même nombre que la dimension) ou bien il suffit de montrer qu’elle est génératrice et qu’elle contient
éléments (le même nombre que la dimension) ou bien il suffit de montrer qu’elle est génératrice et qu’elle contient ![]() éléments.
éléments.
Réponse :
Montrons que ![]() est libre. Pour cela, on se donne trois réels
est libre. Pour cela, on se donne trois réels ![]() et
et ![]() tels que
tels que
![]()
On récupère le système suivant :
![Rendered by QuickLaTeX.com \[\begin{cases} a + c & = 0 \\ b + c & = 0 \\ a + b & =0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0e75a7ddc3cd177e8418838911cc9762_l3.png)
En faisant ![]() on obtient
on obtient
![Rendered by QuickLaTeX.com \[\begin{cases} a + c & = 0 \\ b + c & = 0 \\ b - c & =0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-31f1270f19e21f6c550d8128f9415fde_l3.png)
En sommant les deux dernières lignes, on a ![]() Ainsi
Ainsi ![]() puis
puis ![]() La famille
La famille ![]() est donc libre.
est donc libre.
Remarque : Naurions pu montrer en premier que la famille était génératrice pour en déduire que c’est une base. Mais il est généralement plus facile de montrer que c’est une famille libre.
3. Somme de sous-espaces vectoriels
Méthode 8 : Montrer qu’un espace vectoriel est la somme de deux sous espaces vectoriels.
Soit ![]() un espace vectoriel et soient
un espace vectoriel et soient ![]() deux sous espaces vectoriels de
deux sous espaces vectoriels de ![]()
![]() Pour montrer que
Pour montrer que ![]() on doit montrer que pour tout élément
on doit montrer que pour tout élément ![]() il existe
il existe ![]() et
et ![]() tels que
tels que ![]() On pourra utiliser la méthode d’analyse-synthèse décrite dans la méthode 8.
On pourra utiliser la méthode d’analyse-synthèse décrite dans la méthode 8.
![]() Pour déterminer
Pour déterminer ![]() il faut trouver l’ensemble des
il faut trouver l’ensemble des ![]() de
de ![]() tels qu’il existe
tels qu’il existe ![]() tels que
tels que ![]()
![]() Lorsque de plus
Lorsque de plus ![]() on dit que la somme est directe et on écrit
on dit que la somme est directe et on écrit ![]()
Exemple : Donner une base de ![]() avec
avec ![]() et
et ![]()
Réponse :
Soit ![]() et on cherche des conditions nécessaires et suffisantes sur
et on cherche des conditions nécessaires et suffisantes sur ![]() et
et ![]() pour que
pour que ![]() Le plus simple est de procéder par analyse-synthèse, c’est-à-dire que l’on suppose que
Le plus simple est de procéder par analyse-synthèse, c’est-à-dire que l’on suppose que ![]() et on cherche des conditions nécessaires sur
et on cherche des conditions nécessaires sur ![]() et
et ![]() Lors de la synthèse, on vérifiera que les conditions trouvées lors de l’analyse sont suffisantes.
Lors de la synthèse, on vérifiera que les conditions trouvées lors de l’analyse sont suffisantes.
Analyse : On suppose que ![]() ainsi il existe
ainsi il existe ![]() et
et ![]() tels que
tels que ![]()
Comme ![]() il existe
il existe ![]() tels que
tels que ![]()
![Rendered by QuickLaTeX.com \[\begin{cases} a + c & = x \\ b + d & = y \\ a + d & = z \\ b + c & = t \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c3ce4749a9fe0cfc9e59bce567288379_l3.png)
On rappelle que pout résoudre un tel système, il faut l’échelonner. L’opération ![]() donne :
donne :
![Rendered by QuickLaTeX.com \[\begin{cases} a + c & = x \\ b + d & = y \\ - c + d & = z- x \\ b + c & = t \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cae1058bc3d724b7380b06724ddea6be_l3.png)
Puis en faisant ![]() on a
on a
![Rendered by QuickLaTeX.com \[\begin{cases} a + c & = x \\ b + d & = y \\ - c + d & = z- x \\ c - d & = t - y \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a19690a8d15f3ce5e44fe5a6c5b95dff_l3.png)
Et finalement, en faisant ![]() il vient :
il vient :
![Rendered by QuickLaTeX.com \[\begin{cases} a + c & = x \\ b + d & = y \\ - c + d & = z- x \\ 0 & = -x - y + z + t \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8881a9f0dc80cafd7f52ea09425e0985_l3.png)
La dernière ligne donne ![]() soit
soit ![]()
![]() On note
On note ![]() lorsque
lorsque ![]() est somme directe des sous-espaces
est somme directe des sous-espaces ![]() et
et ![]() on dit alors que
on dit alors que ![]() et
et ![]() sont des supplémentaires de
sont des supplémentaires de ![]()
![]() Soit
Soit ![]() un espace vectoriel et
un espace vectoriel et ![]() deux sous-espaces vectoriels de
deux sous-espaces vectoriels de ![]() Pour montrer que
Pour montrer que ![]() on doit montrer que :
on doit montrer que :
![]()
On rappelle aussi que
![]() si, et seulement si, tout élément
si, et seulement si, tout élément ![]() se décompose de manière unique sous la forme
se décompose de manière unique sous la forme ![]() avec
avec ![]() et
et ![]()
![]() La principale difficulté consiste à prouver que
La principale difficulté consiste à prouver que ![]()
Pour cela, on peut utiliser la méthode d’analyse-synthèse :
![]()
![]() La première phase est l’analyse :
La première phase est l’analyse : ![]() étant un vecteur quelconque de
étant un vecteur quelconque de ![]() on suppose que l’on peut écrire
on suppose que l’on peut écrire ![]() avec
avec ![]() et
et ![]() En utilisant les propriétés des sous-espaces
En utilisant les propriétés des sous-espaces ![]() et
et ![]() on détermine
on détermine ![]() et
et ![]() (on remarquera que si l’on a trouvé par exemple
(on remarquera que si l’on a trouvé par exemple ![]() alors
alors ![]() ).
).
![]()
![]() Puis dans la phase « synthèse », on introduit les vecteurs
Puis dans la phase « synthèse », on introduit les vecteurs ![]() et
et ![]() obtenus dans l’analyse et on vérifie que
obtenus dans l’analyse et on vérifie que ![]() et
et ![]()
![]()
![]() Important : Si dans l’analyse, on a obtenu une unique valeur pour
Important : Si dans l’analyse, on a obtenu une unique valeur pour ![]() et pour
et pour ![]() donc unicité de la décomposition si elle existe, alors on peut conclure à l’issue de la synthèse que
donc unicité de la décomposition si elle existe, alors on peut conclure à l’issue de la synthèse que ![]()
Exemple : Montrer que :
![]() où
où ![]() est l’ensemble des fonctions de
est l’ensemble des fonctions de ![]() dans
dans ![]()
![]() est l’ensemble des fonctions paires de
est l’ensemble des fonctions paires de ![]() dans
dans ![]() et
et ![]() est l’ensemble des fonction impaires de
est l’ensemble des fonction impaires de ![]() dans
dans ![]()
Réponse : Il est facile de voir que ![]() et
et ![]() sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de ![]()
![]()
Puis en utilisant la parité (resp. l’imparité) de ![]() (resp. de
(resp. de ![]() ), on a :
), on a :
![]()
soit
![]()
Cela donne
![]()
On en déduit que si ![]() et
et ![]() existent, elles sont uniques, cela termine l’analyse.
existent, elles sont uniques, cela termine l’analyse.
Synthèse : Il faut vérifier que les fonctions ![]() et
et ![]() trouvées ci-dessus conviennent, c’est-à-dire que
trouvées ci-dessus conviennent, c’est-à-dire que ![]() est paire,
est paire, ![]() est impaire et
est impaire et ![]()
![]()
![]() est donc paire et on montre de la même façon que
est donc paire et on montre de la même façon que ![]() est impaire
est impaire
![]()
![]() Soit
Soit ![]() un espace vectoriel de dimension finie et
un espace vectoriel de dimension finie et ![]() et
et ![]() deux sous-espaces vectoriels de
deux sous-espaces vectoriels de ![]() Pour montrer que
Pour montrer que ![]() il est en général plus simple de montrer que :
il est en général plus simple de montrer que :
![]() et
et ![]()
On retiendra de plus que :
![]() Lorsque
Lorsque ![]() est de dimension
est de dimension ![]() de base
de base ![]() dans le cas où
dans le cas où ![]() les sous-espaces vectoriels
les sous-espaces vectoriels ![]() et
et ![]() sont supplémentaires dans
sont supplémentaires dans ![]()
![]() Si
Si ![]() si
si ![]() est une base de
est une base de ![]() et
et ![]() est une base de
est une base de ![]() alors la famille
alors la famille ![]() est une base de
est une base de ![]() dite adaptée à la somme directe.
dite adaptée à la somme directe.
Exemple : Montrer que :
![]() avec
avec ![]() et
et ![]()
Réponse : On pose ![]() et
et ![]()
![Rendered by QuickLaTeX.com \[\begin{cases} a + b - c & = 0 \\ a + 2 c & = 0 \\ a - b - c & =0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-93ee92235b1720c0cbef14fb79f62339_l3.png)
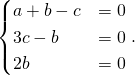 Cela donne
Cela donne 4. Applications linéaires
Méthode 11 : Montrer qu’une application est linéaire.
Soient ![]() et
et ![]() deux
deux ![]() -espaces vectoriels. Soit
-espaces vectoriels. Soit ![]() une application. Pour montrer que
une application. Pour montrer que ![]() est linéaire, en général on revient à la définition, c’est-à-dire que l’on montre que pour tous vecteurs
est linéaire, en général on revient à la définition, c’est-à-dire que l’on montre que pour tous vecteurs ![]() et pour tout
et pour tout ![]()
![]()
Il est aussi possible d’utiliser le fait qu’une combinaison linéaire d’applications linéaires est linéaire et que la composée d’applications linéaires est linéaire (attention quand même aux espaces vectoriels de départ et d’arrivée).
On rappelle que si ![]() et
et ![]() sont de dimension finie, alors
sont de dimension finie, alors ![]() est de dimension finie et
est de dimension finie et
![]()
![]()
![]()
Piège : Lorsque l’on demande de montrer qu’une application ![]() est un endomorphisme de
est un endomorphisme de ![]() , on doit montrer :
, on doit montrer :
![]() la linéarité de
la linéarité de ![]() ,
,
![]() si
si ![]() alors
alors ![]()
\noindent Le dernier point est trop souvent oublié.
Exemple : Montrer que les applications suivantes sont linéaires :
1) ![]() définie par : pour tout
définie par : pour tout ![]()
![]()
2) ![]() définie par : pour tout
définie par : pour tout ![]()
![]() est le reste de la division euclidienne de
est le reste de la division euclidienne de ![]() par
par ![]()
Réponse :
1) Soit ![]() Cela signifie que le degré de
Cela signifie que le degré de ![]() est inférieur à
est inférieur à ![]() Celui de
Celui de ![]() est donc inférieur à
est donc inférieur à ![]() et donc celui de
et donc celui de ![]() est inférieur à
est inférieur à ![]() Ainsi
Ainsi ![]()
Soient ![]() et
et ![]() On a
On a
![]()
![]()
![]()
![]()
![]()
![]() .
.
Ainsi ![]() est un endomorphisme de
est un endomorphisme de ![]()
2) Soient ![]() et
et ![]() montrons que
montrons que ![]() Ici l’expression de
Ici l’expression de ![]() n’est pas explicite comme dans les deux premiers exemples. Faisons la division euclidienne de
n’est pas explicite comme dans les deux premiers exemples. Faisons la division euclidienne de ![]() et
et ![]() par
par ![]() : il existe
: il existe ![]() et
et ![]() dans
dans ![]() tels que :
tels que :
![]()
et
![]()
En multipliant la deuxième ligne par ![]() et en sommant les lignes, on a :
et en sommant les lignes, on a :
Par unicité du reste de la division euclidienne de
![]()
Ainsi ![]() est un endomorphisme de
est un endomorphisme de ![]()
Dans certains exercices, on vous demandera de définir une application linéaire vérifiant certaines conditions. Il peut être utile de définir alors l’application linéaire seulement sur une base (éventuellement bien choisie). La linéarité permettant de la définir sur tout l’espace.
En effet, soit ![]() une application linéaire entre deux
une application linéaire entre deux ![]() -espaces vectoriels
-espaces vectoriels ![]() et
et ![]() Supposons que l’on connaisse
Supposons que l’on connaisse ![]() sur une base de
sur une base de ![]() disons
disons ![]() Alors si
Alors si ![]() on peut écrire
on peut écrire ![]() avec
avec ![]() Ainsi
Ainsi 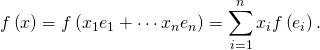
On a la conséquence suivante très intéressante : pour montrer que deux applications ![]() et
et ![]() linéaires sont égales, il suffit de vérifier qu’elles sont égales sur les éléments d’une base.
linéaires sont égales, il suffit de vérifier qu’elles sont égales sur les éléments d’une base.
Exemple : Soit ![]() un espace vectoriel de dimension finie. Soit
un espace vectoriel de dimension finie. Soit ![]() un sous espace vectoriel de
un sous espace vectoriel de ![]() Montrer qu’il existe un endomorphisme de
Montrer qu’il existe un endomorphisme de ![]() dont
dont ![]() soit le noyau.
soit le noyau.
Réponse : Si ![]() l’application
l’application ![]() convient. Dans la suite, on suppose que
convient. Dans la suite, on suppose que ![]() On note
On note ![]() et on se donne
et on se donne ![]() une base de
une base de ![]() . On complète cette famille libre en une base notée
. On complète cette famille libre en une base notée ![]() de
de ![]() grâce au théorème de la base incomplète.
grâce au théorème de la base incomplète.
On définit ![]() de la façon suivante :
de la façon suivante :
![]() si
si ![]() et
et ![]() si
si ![]()
Si ![]() est une application linéaire entre deux espaces vectoriels
est une application linéaire entre deux espaces vectoriels ![]() et
et ![]() le noyau de
le noyau de ![]() noté
noté ![]() est le sous-espace vectoriel de
est le sous-espace vectoriel de ![]() défini par :
défini par :
![]()
Le noyau est généralement facile à déterminer, il suffit de résoudre l’équation ![]()
Remarque : Une application linéaire est injective si et seulement si ![]() Dès que l’on rencontre une question portant sur l’injectivité d’une application linéaire, il faut faire le lien avec le noyau.
Dès que l’on rencontre une question portant sur l’injectivité d’une application linéaire, il faut faire le lien avec le noyau.
Exemple :
Déterminer le noyau des applications linéaires suivantes :
1) ![]() définie par
définie par ![]()
2) ![]() définie par
définie par ![]()
Réponse :
1) Soit ![]() On a donc :
On a donc : ![]() ainsi on a le système suivant :
ainsi on a le système suivant :
![Rendered by QuickLaTeX.com \[\begin{cases} x + y & = 0 \\ x -y & = 0 \\ x + 2y & = 0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-423a1edde59b434523613c624bc2020e_l3.png)
La somme des deux premières lignes donne : ![]() puis
puis ![]() et
et ![]() Ainsi
Ainsi ![]() L’inclusion contraire est évidente, donc
L’inclusion contraire est évidente, donc ![]()
En particulier, cela montre que ![]() est injective.
est injective.
2) Soit ![]() cela signifie que
cela signifie que ![]() soit
soit
![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Soient ![]() un espace vectoriel de dimension finie et
un espace vectoriel de dimension finie et ![]() un espace vectoriel (pas nécessairement de dimension finie) et
un espace vectoriel (pas nécessairement de dimension finie) et ![]() Le théorème du rang donne la relation
Le théorème du rang donne la relation
![]()
![]()
En conséquence, pour démontrer que ![]() il suffira de montrer que
il suffira de montrer que ![]() et d’utiliser le théorème du rang lorsque
et d’utiliser le théorème du rang lorsque ![]() est une espace vectoriel de dimension finie.
est une espace vectoriel de dimension finie.
Remarque : Le théorème du rang ne veut pas dire que ![]() !
!
Exemple : Soient ![]() un espace vectoriel de dimension finie et
un espace vectoriel de dimension finie et ![]() Montrer l’équivalence entre les propriétés
Montrer l’équivalence entre les propriétés
i) ![]()
ii) ![]()
iii) ![]()
Réponse : On va prouver que i) ![]() ii)
ii) ![]() iii)
iii) ![]() i).
i).
![]() On suppose que
On suppose que ![]()
![]()

