Chapitres Maths en ECG1
Chapitres Maths en ECG1
Exercices : Convergences et approximations en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Inégalités classiques & Convergences de suites de variables aléatoires
Exercice :
1) Si 
et 
on pose 
a) Montrer que 
b) Montrer que l’intégrale 
est convergente.
c) Calculer 
d) à l’aide d’une intégration par parties, montrer que 
; en déduire la valeur de 
2) Pour 
on définit la fonction 
par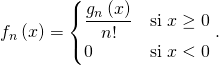 
a) Montrer que est une densité.
On note à présent 
une variable aléatoire réelle admettant pour densité. On note 
la fonction de répartition de 
b) La variable admet-elle une espérance ?
c) Calculer, pour 
et 
d) Calculer 
pour 
e) Soit 
et 
montrer que 
En déduire une expression de 
pour et faisant intervenir une somme que l’on ne cherchera pas à calculer.
f) Pour 
déterminer la limite de la suite 
g) La suite de variables aléatoires 
converge-t-elle en loi ?
3) Pour on note 
On admet que 
est une variable aléatoire.
a) Montrer que est bien définie. Quelles pour les valeurs prises par ?
b) On note 
la fonction de répartition de 
Montrer que pour tout réel 
c) Montrer que est une variable à densité et donner une densité de
d) Justifier que admet une espérance et la calculer.
e) Justifier que admet une variance et la calculer.
f) Reconnaître la loi de 
à l’aide de ce qui précède, déterminer 
pour 
g) Montrer que la suite de variables aléatoires de terme général 
converge en probabilité vers une variable aléatoire constante.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Pour intensifier vos révisions en maths en ECG1, testez-vous dès maintenant sur tous les exercices de nos cours en ligne de maths d’ECG1 :