Chapitres de maths en 1ère

Exercices sur la fonction exponentielle en première

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Première

Ces exercices sur la fonction exponentielle en 1ère permettent aux élèves de réviser le cours en ligne de maths en première.

Des exercices sur les autres chapitres de première sont également disponibles : des exercices sur les suites numériques, des exercices sur les suites arithmétiques et géométriques, des exercices sur le second degré, etc.

Fonction exponentielle : exercice 1

Simplifier les expressions suivantes pour obtenir une expression de la forme $e^a$ :

Question 1

$e^{-5}\times \dfrac{1}{e^{-3}}\times e$

Question 2

$\dfrac{e^{10}}{-e^{-2}}\times \dfrac{-e^{-4}}{e^{8}}$

Question 3

$e^3(e^{-3}-e^2)+e^2(e^3+e)-1$

COURS PARTICULIERS 1ÈRE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers pour la Première.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 1 sur la fonction exponentielle

Question 1

$e^{-5}\times \dfrac{1}{e^{-3}}\times e$

$=e^{-5}\times e^{3}\times e^1$

$=e^{-5+3+1}$

$=e^{-1}$

Question 2

$\dfrac{e^{10}}{-e^{-2}}\times \dfrac{-e^{-4}}{e^{8}}$

$=(-e^{10}\times e^2)\times (-e^{-4}\times e^{-8})$

$=(-e^{10+2})\times(-e^{-4-8})$

Ce qui donne, $\dfrac{e^{10}}{-e^{-2}}\times \dfrac{-e^{-4}}{e^{8}}=e^{12-12}=e^0$

Question 3

On a les égalités suivantes:

$e^3(e^{-3}-e^2)+e^2(e^3+e)-1$

$=e^3\times e^{-3}-e^3\times e^2+e^2\times e^3+e^2\times e-1$

$=e^{3-3}-e^{3+2}+e^{2+3}+e^{2+1}-1$

$=1+e^3-1$

$=e^3$

Fonction exponentielle : exercice 2

Résoudre dans $\mathbb{R}$ l’inéquation:

Question 1

$e^x> e^{-x}$ .

Question 2

$e^{2x+1}>1$ .

Question 3

$e^{5x^2-12x}>e^{2x-4}$ .

STAGE INTENSIF 1ÈRE

Profite de tes vacances pour gagner des points au bac.

96% de progression à l’issue du stage 1ère
54% de mention Bien et Très Bien au bac
99% de satisfaction des familles et élèves

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 2 sur la fonction exponentielle

Question 1

On utilisera la propriété suivante :

Pour tout $a\in\mathbb{R}$ , tout $b\in\mathbb{R}$ , $\mathbf{a < b \Leftrightarrow e^a < e^b}$

$e^x > e^{-x}$

Pour tout $x\in\mathbb{R}$ , $e^x > e^{-x} \Leftrightarrow x > -x \Leftrightarrow 2x > 0 \Leftrightarrow x > 0$

Alors, l’ensemble de solution est: $]0;+\infty[$ .

Question 2

$e^{2x+1} > 1$

Pour tout $x\in\mathbb{R}$ , $e^{2x+1} > e^0 \Leftrightarrow 2x+1 > 0 \Leftrightarrow x > -\dfrac{1}{2}$

Donc, l’ensemble de solutions est : $]-\dfrac{1}{2};+\infty[$

Question 3

$e^{5x^2-12x} > e^{2x-4}$

Pour tout $x\in\mathbb{R}$ ,

$e^{5x^2-12x} > e^{2x-4}$

$\Leftrightarrow 5x^2-12x > 2x-4$

$\Leftrightarrow 5x^{2}-14x+4>0$

Le discriminant du polynôme $P$ avec $P(x)=5x^2 - 14x + 4$ vaut

$\Delta = 14^2 - 4\times 5\times 4$

$= 196 - 80$

$= 116$ . Donc, $P$ admet deux racines:

$x_1 =\dfrac{-b+\sqrt{\Delta}}{2a}$

$=\dfrac{14+\sqrt{116}}{10}$

$= \dfrac{14 + 2\sqrt{29}}{10}$

$= \dfrac{7+\sqrt{29}}{5}$

$x_2 = \dfrac{-b-\sqrt{\Delta}}{2a}$

$= \dfrac{14-2\sqrt{29}}{10}$

$= \dfrac{7-\sqrt{29}}{5}$

Fonction exponentielle : exercice 3

Soit $f$ la fonction définie par :

$f(x)=\frac{e^x-e^{-x}}{e^x+1}, x\in \mathbb{R}$

Question 1

Justifier la dérivabilité de $f$ sur $\mathbb{R}.$

Question 2

Démontrer que pour tout réel $x$ , $f'(x)=e^{-x}$ où la fonction $f'$ est la fonction dérivée de $f$

Question 3

Dresser le tableau de variation complet de $f$ sur $\mathbb{R}$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 3 sur la fonction exponentielle

(voir les exercices sur la dérivation en première)

Question 1

Les fonctions $x\longmapsto e^x-e^{-x}$ et $x\longmapsto e^x+1$ sont deux fonctions définies et dérivables sur $\mathbb{R}$ ,

et pour tout $x\in \mathbb{R}, e^x+1>0$ donc $f$ est dérivable sur $\mathbb{R}$ .

Question 2

L’expression $f(x)$ est de la forme $\dfrac{u(x)}{v(x)}$ , avec:

$u(x) = e^x-e^{-x}$

$u'(x) = e^x+e^{-x}$

$v(x) = e^x+1$

$v'(x) = e^x$

Alors, pour tout $x\in\mathbb{R}$ ,

$f'(x) = \dfrac{u'(x)v(x) - u(x)v'(x)}{\left(v(x)\right)^2}$

$= \dfrac{(e^x+e^{-x})(e^x+1) - (e^x-e^{-x})e^x}{(e^x+1)^2}$

$= \dfrac{e^{2x}+e^x+1+e^{-x}-e^{2x}+1}{(e^x+1)^2}$

$= \dfrac{e^x+e^{-x}+2}{(e^x+1)^2}$

$= \dfrac{e^{-x}\left(\left(e^x\right)^2+1+2e^{x}\right)}{(e^x+1)^2}$

$= e^{-x}\dfrac{(e^x+1)^2}{(e^x+1)^2}$

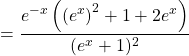
d’où $f'(x) = e^{-x}$

Question 3

Tableau de variation de $f$ sur $\mathbb{R}$ .

Pour tout $x\in \mathbb{R}, e^{-x}>0$ , donc pour tout $x\in \mathbb{R}, f'(x)>0$ . On a le tableau de variation de $f$ sur $\mathbb{R}$ :

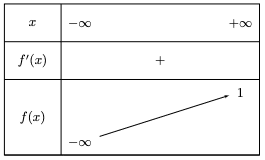
D’autres exercices plus complets sur la fonction exponentielle sont disponibles sur notre application mobile PrepApp qui contient également des cours et des exercices sur les autres matières du programme de première.

Exercices sur la fonction exponentielle en première

Fonction exponentielle : exercice 1

Question 1

Question 2

Question 3

COURS PARTICULIERS 1ÈRE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers pour la Première.

POUR ACCÉLÉRER MA PROGRESSION

Correction de l’exercice 1 sur la fonction exponentielle

Question 1

Question 2

Question 3

Fonction exponentielle : exercice 2

Question 1

Question 2

Question 3

STAGE INTENSIF 1ÈRE

Profite de tes vacances pour gagner des points au bac.

Correction de l’exercice 2 sur la fonction exponentielle

Question 1

Question 2

Question 3

Fonction exponentielle : exercice 3

Question 1

Question 2

Question 3

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Correction de l’exercice 3 sur la fonction exponentielle

Question 1

Question 2

Question 3

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales