Mon parcours pour réussir en maths
J'aprends le cours par coeur
Je travaille avec un prof de maths
Je travaille entre chaque séance
Avis Google France
★★★★★ 4,8 sur 5
Exercices corrigés sur les pourcentages en seconde
Résumé de cours Exercices et corrigés
Cours en ligne de Seconde Générale
Les exercices sur les pourcentages et les informations chiffrées sont un chapitre essentiel en seconde et en première en maths spécialité. Ils vous permettentt d’approfondir votre compréhension des mathématiques de manière concrète et pratique. Dans un monde de plus en plus axé sur les données, maîtriser ces notions est non seulement avantageux pour exceller dans les cours de mathématiques, mais aussi important pour la vie quotidienne et les carrières futures. Pour renforcer davantage vos acquis, envisager le soutien d’un professeur de maths peut être une option judicieuse. Ce type d’accompagnement personnalisé, adapté à votre niveau, cible spécifiquement les domaines d’amélioration, surmonte les difficultés et encourage une compréhension approfondie des notions fondamentale au lycée.
Exercice 1 de conversion entre pourcentages, fractions et nombres en seconde
Écrire les nombres suivants sous forme de pourcentage, arrondi à ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Déterminer sous forme de fraction les quantités suivantes:
![]() de
de ![]() de 70 000 000;
de 70 000 000;
![]() de
de ![]() de 9 000;
de 9 000;
![]() du tiers de 150;
du tiers de 150;
![]() de
de ![]() des 1 000 000 000 d’euros;
des 1 000 000 000 d’euros;
![]() du quart des 365 jours.
du quart des 365 jours.
Avis Google France ★★★★★ 4,9 sur 5COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité En ligne ou à domicile
Exercice 2 de maths : Analyse de l’évolution des effectifs en 2nde
Le tableau ci-après montre l’évolution annuelle des effectifs des animaux dans un Zoo.
Initialement, on compte 200 animaux.
On note :
![]() pour
pour ![]() allant de
allant de ![]() à
à ![]() , le taux d’évolution entre les périodes
, le taux d’évolution entre les périodes ![]() et
et ![]() .
.
Par exemple, ![]() ;
;
![]() le coefficient multiplicateur entre les périodes
le coefficient multiplicateur entre les périodes ![]() et
et ![]() pour
pour ![]() allant de
allant de ![]() à
à ![]() .
.
Par exemple, ![]()

Déterminer les taux d’évolution successifs ![]() et
et ![]() .
.
Déterminer les coefficients multiplicateurs ![]() et
et ![]() .
.
En déduire le coefficient multiplicateur global noté ![]() et le taux d’évolution global noté
et le taux d’évolution global noté ![]() .
.
Exercice 3 : Étude de l’évolution des salaires et du pouvoir d’achat en seconde
Le premier janvier ![]() , la direction d’une entreprise a annoncé une augmentation des salaires de
, la direction d’une entreprise a annoncé une augmentation des salaires de ![]() à partir de cette date.
à partir de cette date.
Fin mai ![]() , suite à des bonnes nouvelles favorables aux activités de l’entreprise, la direction a encore augmenté les salaires de
, suite à des bonnes nouvelles favorables aux activités de l’entreprise, la direction a encore augmenté les salaires de ![]() .
.
A- Evolution des salaires
Pour un salarié qui perçoit 1 750 € par mois en décembre 2020 :
A-1) Calculer le montant de son salaire en fin janvier 2021.
A-2) Calculer le montant de son salaire en fin mai 2021.
A-3) Calculer le montant de son salaire en fin juin 2021.
A-4) Calculer le montant de son salaire en fin décembre 2021.
A-5) Calculer le taux d’augmentation global de son salaire durant l’année 2021.
B- Evolution du pouvoir d’achat
Durant l’année ![]() , le niveau général des prix a augmenté de
, le niveau général des prix a augmenté de ![]() .
.
Le coefficient multiplicateur du pouvoir d’achat est déterminé par la formule:
CM du Pouvoir d’Achat = ![]()
B-1) Calculer le taux d’augmentation mensuel moyen du niveau des prix.
B-2) En décembre 2021, le pouvoir d’achat d’un salarié a-t-il réellement augmenté? Justifier.
Exercice 4 en 2nde : Vrai ou faux sur la logique et le raisonnement en maths
Dire si l’affirmation est vraie ou fausse. Démontrer votre réponse.
1. On peut avoir un coefficient multiplicateur nul.
2. Le pourcentage d’un pourcentage est un pourcentage.
3. Le coefficient multiplicateur peut prendre toutes les valeurs réelles.
4. Le coefficient multiplicateur global est toujours supérieur à la somme des coefficients multiplicateurs successifs.
5. Le taux d’évolution global est supérieur à la somme des taux d’évolution successifs divisée par le nombre de périodes.
6. Il existe un taux d’évolution ![]() tel que si
tel que si ![]() est son taux réciproque,
est son taux réciproque, ![]() .
.
STAGE INTENSIF SECONDE
Travailler les maths en seconde générale en stage de vacances
–> Stage de perfectionnement ou de remise à niveau
–> Préparer la spécialité maths dès la 2nde
–> Petits groupes en stage de maths en seconde
Avis Google France ★★★★★ 4,9 sur 5
Corrigé de l’exercice 1 :conversion entre pourcentages, fractions et nombres
1. Le pourcentage est obtenu par la multiplication par 100
![]() soit environ
soit environ ![]() ;
;
![]() soit environ
soit environ ![]() ;
;
![]() soit
soit ![]() ;
;
![]() soit environ
soit environ ![]() ;
;
![]() .
.
2. On a :
a) ![]() de
de ![]() de 70 000 000.
de 70 000 000.
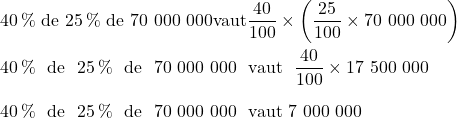
Donc, ![]() de
de ![]() de 70 000 000 donne 7 000 000, soit
de 70 000 000 donne 7 000 000, soit ![]() sous forme de fraction.
sous forme de fraction.
b) ![]() de
de ![]() de 9 000.
de 9 000.
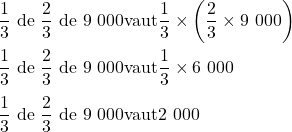
Donc, ![]() de
de ![]() donne 9 000, soit
donne 9 000, soit ![]() sous forme de fraction.
sous forme de fraction.
c) ![]() du tiers de 150.
du tiers de 150.

Donc, ![]() donne 150,
donne 150, ![]() sous forme de fraction.
sous forme de fraction.
d) ![]() de
de ![]() des 1 000 000 000 d’euros.
des 1 000 000 000 d’euros.
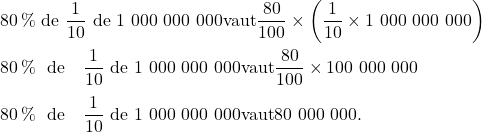
Donc, ![]() de
de ![]() donne 1 000 000 000 d’euros, soit
donne 1 000 000 000 d’euros, soit ![]() sous forme de fraction.
sous forme de fraction.
e) ![]() du quart des 365 jours.
du quart des 365 jours.

Donc, ![]() du quart des 365 vaut
du quart des 365 vaut ![]() jours ce qui est équivalent à 4 jours 1 heure et 30 minutes.
jours ce qui est équivalent à 4 jours 1 heure et 30 minutes.
Réponse à l’exercice 2 sur l’analyse de l’évolution des effectifs en 2nde
On a un tableau de l’évolution annuelle des effectifs des animaux dans un Zoo.
En appliquant la formule ![]() pour calculer les taux d’évolution
pour calculer les taux d’évolution ![]() ,
,
on a :
![]() soit +87,5 %;
soit +87,5 %;
![]() soit +6,25 %;
soit +6,25 %;
![]() soit -50 %;
soit -50 %;
![]() soit +200 %.
soit +200 %.
Par la formule ![]() , on a :
, on a :
![]() soit 1,875;
soit 1,875;
![]() soit 1,0625;
soit 1,0625;
![]() soit 0,5;
soit 0,5;
![]() soit 3.
soit 3.
Sachant que le coefficient multiplicateur global est le produit des coefficients multiplicateurs successives et que le taux d’évolution global ![]() ,
,
On déduit que :
![]()
![]()
![]()
![]()
En résumé, on obtient le tableau suivant :

Correction exercice 3 : Étude de l’evolution des salaires et du pouvoir d’achat
Le premier janvier ![]() , la direction d’une entreprise a annoncé une augmentation des salaires de
, la direction d’une entreprise a annoncé une augmentation des salaires de ![]() à partir de cette date.
à partir de cette date.
Fin mai ![]() , suite à des bonnes nouvelles favorables aux activités de l’entreprise, la direction a encore augmenté les salaires de
, suite à des bonnes nouvelles favorables aux activités de l’entreprise, la direction a encore augmenté les salaires de ![]() .
.
A- Evolution des salaires
Pour un salaire de valeur initiale ![]() , après augmentation de
, après augmentation de ![]() , le salaire devient :
, le salaire devient :

Pour un salarié qui perçoit 1 750 \euro{} par mois en décembre 2020:
A-1) A la fin du mois de janvier, son salaire a augmenté de ![]() .
.
Donc, le montant de son salaire le trente et un janvier ![]() est de
est de ![]() soit
soit ![]() \euro.
\euro.
A-2) Fin mai 2021, le montant de son salaire est le même qu’en janvier 2021.
A-3) Fin juin 2021, après l’augmentation de ![]() , son salaire devient
, son salaire devient ![]() soit 1 776,3375 \euro.
soit 1 776,3375 \euro.
A-4) Fin décembre 2021, c’est identique à son salaire à la fin du mois de 2021.
A-5) Après ces deux augmentations ayant pour coefficients multiplicateurs respectifs 1,01 et 1,005, le coefficient multiplicateur global de son salaire vaut ![]() .
.
Donc, le taux d’augmentation global de son salaire durant l’année 2021 est ![]() soit 1,505 %.
soit 1,505 %.
B- Evolution du pouvoir d’achat
Durant l’année ![]() , le niveau général des prix a augmenté de
, le niveau général des prix a augmenté de ![]() .
.
B-1) Le taux mensuel moyen est l’équivalent d’une augmentation mensuelle au même taux durant les douze mois de l’année.
On note ![]() le taux mensuel moyen,
le taux mensuel moyen, ![]() le taux d’augmentation de l’année, CM le coefficient multiplicateur global et CM
le taux d’augmentation de l’année, CM le coefficient multiplicateur global et CM![]() le coefficient multiplicateur moyen.
le coefficient multiplicateur moyen.
Alors :
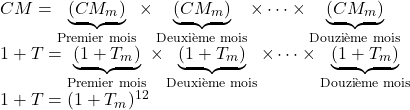
Donc, le taux moyen mensuel ![]() est la solution de l’équation
est la solution de l’équation
![]()
![Rendered by QuickLaTeX.com 1,04=(1+T_m)^{12} \Longleftrightarrow & \left[(1+T_m)^{12}\right]^{\frac{1}{12}}=(1,04)^{\frac{1}{12}} \\ 1,04=(1+T_m)^{12} \Longleftrightarrow & 1+T_m=(1,04)^{\frac{1}{12}} \\ 1,04=(1+T_m)^{12} \Longleftrightarrow & T_m=(1,04)^{\frac{1}{12}}-1 \\ 1,04=(1+T_m)^{12} \Longleftrightarrow & T_m\approx 1,0033-1](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-94e064a71c5784af65f38d9dde1ca718_l3.png)
Alors, le taux d’augmentation mensuel moyen du niveau des prix est approximativement égal à 0,0033 soit une augmentation moyenne de 0,33 %.
B-2) A partir de la formule :
CM du Pouvoir d’Achat = ![]()
On obtient:
CM du Pouvoir d’Achat = ![]()
CM du Pouvoir d’Achat ![]()
Vu que CM du pouvoir d’achat est plus petit que ![]() , alors l’augmentation des salaires n’a pas compensé l’augmentation des prix.
, alors l’augmentation des salaires n’a pas compensé l’augmentation des prix.
Le salaire a perdu en pouvoir d’achat. D’une autre manière, le salaire a augmenté mais il s’est appauvri !
Remarque
Si ![]() est une inconnue d’une équation de la forme
est une inconnue d’une équation de la forme ![]() ,
,
![]() et
et ![]() alors
alors ![]() .
.
Ce qui se lit, ![]() est la racine
est la racine ![]() ième de
ième de ![]() .
.
Par exemple, pour ![]() ,
, ![]() est la racine carrée positive de
est la racine carrée positive de ![]() .
.
Si ![]() ,
, ![]() est la racine cubique de
est la racine cubique de ![]() etc.
etc.
Avis Google France ★★★★★ 4,9 sur 5COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Corrigé exercice 4 en 2nde: Vrai ou faux sur la logique et le raisonnement en maths
1. Non. Par l’absurde
Cette affirmation est une affirmation existentielle – affirme l’existence de quelque chose – alors il suffit de trouver un objet satisfaisant les conditions imposées.
Par exemple avec une valeur initiale ![]() et une valeur finale
et une valeur finale ![]() ,
,
On obtient :
![]()
C’est l’équivalent d’une baisse de ![]() .
.
2. Faux. Un contre-exemple
Le pourcentage est défini par :
Pourcentage=![]()
Avec les deux pourcentages comme ![]() et
et ![]() , le produit des nombres vaut
, le produit des nombres vaut ![]() mais le produit
mais le produit ![]() n’a pas de sens.
n’a pas de sens.
3. Faux.
Si ![]() est un réel négatif, on ne peut pas le définir comme un coefficient multiplicateur qui est un rapport de deux nombres positifs.
est un réel négatif, on ne peut pas le définir comme un coefficient multiplicateur qui est un rapport de deux nombres positifs.
4. Faux. Un contre exemple.
On considère quatre périodes notées ![]() et 3.
et 3.
On prend les coefficients multiplicateurs ![]() et
et ![]() .
.
Le coefficient multiplicateur est multiplicatif alors le coefficient multiplicateur global
![]() .
.
Or, ![]() .
.
Donc, la somme des multiplicateurs successifs est supérieure au coefficient multiplicateur global. Ce qui contredit l’assertion de l’énoncé.
5. Faux. Par un contre-exemple.
On considère trois périodes notées ![]() et
et ![]() .
.
Soient ![]() le taux d’évolution global et
le taux d’évolution global et ![]() et
et ![]() les taux d’évolution entre les périodes
les taux d’évolution entre les périodes ![]() et
et ![]() et les périodes
et les périodes ![]() et
et ![]() .
.
Le coefficient multiplicateur est multiplicatif, alors :
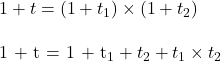
Maintenant, on suppose que l’assertion est vraie. Donc ![]() .
.
Ce qui donne ![]() .
.
Ce qui est équivalent à ![]() .
.
C’est-à-dire, ![]() .
.
Ainsi, il suffit de prendre ![]() et
et ![]() pour conclure.
pour conclure.
C’est une hausse de ![]() et une baisse de
et une baisse de ![]() .
.
6. Vrai. Raisonnement direct.
Soit ![]() un taux d’évolution associé à un coefficient multiplicateur
un taux d’évolution associé à un coefficient multiplicateur ![]() .
.
Alors, le coefficient multiplicateur réciproque est ![]() .
.
Donc, le taux réciproque de ![]() est
est ![]() .
.
Ce qui donne ![]() .
.
Donc :
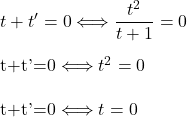
Ainsi, il existe un taux d’évolution ![]() tel que si
tel que si ![]() est son taux d’évolution réciproque,
est son taux d’évolution réciproque, ![]() .
.
Consultez nos exercices en ligne de maths en seconde générale :
- Exercices et corrigés : Statistiques en seconde
- Exercices et corrigés maths en seconde : Probabilités
- Entrainement en maths sur ensembles et intervalles
- Exercices et corrigés arithmétique en 2nde
- Exercices corrigés fonctions seconde en maths
- Résumé de cours gratuit : statistiques seconde
- Réussir en seconde sur les probabilités en maths

