Cours en ligne Physique-Chimie en Maths Spé
Chapitres Physique-Chimie en MP, PSI, PC, MPI, TSI, PT
Exercices et corrigés sur la physique quantique en maths spé
Résumé de cours Exercices et corrigés
Ces exercices corrigés pour la maths spé en physique chimie sur la physique quantique pourront vous aider à mieux comprendre les notions sur Pseudo-OPPH, Vitesse de groupe, vitesse de phase. En plus de ces exercices et corrigés que vous pouvez faire en autonomie, Groupe Réussite propose si vous souhaitez cibler des concours comme X/ENS, Centrale Supelec ou encore Mines Ponts l’aide d’un prof de physique chimie. Au quotidien, l’enseignant à domicile ou en ligne vous proposera des résumés de cours et des séries d’exercices ou d’annales ciblées pour répondre à vos problématiques et vous faire gagner des points aux différentes épreuves.
QCM sur la physique quantique en maths spé
Question 1 :
Le terme spatial ![]() de la solution stationnaire est
de la solution stationnaire est
a. toujours une exponentielle complexe ou réelle
b. toujours une exponentielle complexe
c. toujours une exponentielle réelle
d. parfois une fonction qui n’est ni exponentielle complexe ni exponentielle réelle.
Question 2 :
Une onde progressive harmonique définie sur ![]() solution de l’EDS
solution de l’EDS
a. est non normalisable et de largeur spectrale non nulle
b. est non normalisable et de largeur spectrale nulle
c. est normalisable et de largeur spectrale non nulle
d. est normalisable et de largeur spectrale nulle
Tu veux réussir en physique chimie ?
Accède aux meilleurs exercices et résumés de cours
Travaille sur les annales en autonomie
Fais toi accompagner en cours à domicile
Les élèves que nous aidons en cours de physique -chimie à domicile recommandent à 98% nos profs
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du QCM de maths spé sur la physique quantique
Question 1 :
La bonne réponse est la d.
![]() est exponentielle réelle ou complexe quand
est exponentielle réelle ou complexe quand ![]() est constante sur un intervalle, mais peut être une autre fonction si
est constante sur un intervalle, mais peut être une autre fonction si ![]() n’est pas une fonction en escaliers.
n’est pas une fonction en escaliers.
Question 2 :
La bonne réponse est b.
Exercices sur la physique quantique en maths spé
Exercice sur le paquet d’ondes.
Un paquet d’ondes possède un spectre continu dont la densité spectrale est
![]()
où ![]() est l’amplitude de la solution stationnaire de l’EDS, et dont la fonction d’onde est une somme intégrale
est l’amplitude de la solution stationnaire de l’EDS, et dont la fonction d’onde est une somme intégrale
![]()
![]()
![]()
Un paquet d’ondes possède un profil spectral rectangulaire
![]() pour
pour ![]()
et nulle partout ailleurs.
1. Pour ![]() , donner l’expression de la pulsation
, donner l’expression de la pulsation
![]() et de sa dérivée
et de sa dérivée
![]()
En fonction de ![]() et de la masse
et de la masse ![]() de la particule.
de la particule.
2. On fait le développement limité au premier ordre
![]()
Soit ![]()
On pose ![]() et
et ![]() .
.
Écrire la fonction d’onde sous la forme
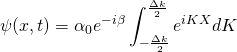
Où on donnera l’expression de ![]() en fonction de
en fonction de ![]() et de
et de ![]() .
.
3. En calculant explicitement l’intégrale, montrer que
![]()
Avec ![]()
Et en déduire l’expression de la densité linéïque de probabilité ![]() .
.
4. La fonction ![]() passe par un maximum absolu égal à 1 pour
passe par un maximum absolu égal à 1 pour ![]() . Expliquer pourquoi
. Expliquer pourquoi ![]() est la vitesse de groupe.
est la vitesse de groupe.
Tu veux réussir en physique ?
Un suivi assidu et des tarifs justes
Des enseignants certifiés et étoilés
Un environnement favorable à la concentration
Des milliers de parents et d’élèves sont satisfaits de leur accompagnement
Avis Google France
★★★★★ 4,9 sur 5
Exercice sur la marche de potentiel de hauteur inférieure à l’énergie.
Une particule de masse ![]() , d’énergie
, d’énergie ![]() , est soumise à un champ de forces qui dérive de l’énergie potentielle
, est soumise à un champ de forces qui dérive de l’énergie potentielle
![]() pour
pour ![]()
![]() pour
pour ![]()
1. Donner l’expression des solutions stationnaires en notant ![]() et
et ![]() les amplitudes des ondes se propageant dans le sens des
les amplitudes des ondes se propageant dans le sens des ![]() croissants et
croissants et ![]() et
et ![]() l’amplitude de celles se propageant dans l’autre sens.
l’amplitude de celles se propageant dans l’autre sens.
On posera
![]() et
et ![]()
2. On considère un faisceau de particules venant de ![]()
Déterminer les coefficients ![]() et
et ![]()
3. En déduire les coefficients de réflexion ![]() et de transmission
et de transmission ![]() en courant de probabilités.
en courant de probabilités.
4. Application : un faisceau de particules homocinétiques est formé de 98,000 pourcents d’ions X de masse ![]() et d’énergie
et d’énergie ![]() et de 2,000 pourcents d’ions de masse
et de 2,000 pourcents d’ions de masse ![]() et d’énergie
et d’énergie ![]() . On prend
. On prend ![]() .
.
Quel est le pourcentage des ions formant le faisceau transmis ?
Corrigé des exercices la physique quantique en maths spé
Corrigé sur le paquet d’ondes.
1. La relation de dispersion s’écrit
![]()
Donc
![]()
On en déduit la vitesse de groupe
![]()
![]()
2. On calcule l’intégrale dans l’intervalle de non nullité, en remplaçant ![]() et
et ![]() par les expressions fournies
par les expressions fournies
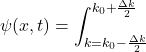
![]()
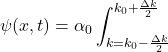
![]()
Effectuons le changement de variable d’intégration proposé par l’énoncé
![]() donc
donc ![]() et
et ![]()
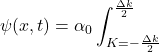
![]()
![]()
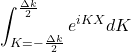
On retrouve donc bien la formule donnée par l’énoncé avec
![]() .
.
3. Le calcul de l’intégrale est simple :
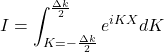
![Rendered by QuickLaTeX.com \displaystyle{I=\left[\frac1{iK}e^{iKX}\right]_{-\frac{\Delta k}{2}}^{\frac{\Delta k}{2}}}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-28c7de8d0690dfb549ccedccb6b4944a_l3.png)
![]()
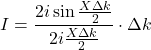
![]()
Donc
![]()
Qui est bien la forme attendue. La densité linéïque de probabilité est, par définition :
![]()
![]()
4. Le pic de probabilité correspond au maximum de ![]() , et est donc atteint, à la date
, et est donc atteint, à la date ![]() , lorsque
, lorsque ![]() (maximum de la fonction sinus cardinal carré), soit
(maximum de la fonction sinus cardinal carré), soit
![]() soit
soit ![]()
![]() est donc la vitesse de déplacement du maximum de la fonction
est donc la vitesse de déplacement du maximum de la fonction ![]() , c’est donc celle de déplacement du paquet d’onde, ce qui est bien la définition de la vitesse de groupe.
, c’est donc celle de déplacement du paquet d’onde, ce qui est bien la définition de la vitesse de groupe.
STAGE EN MATHS SPÉ
Le meilleur stage intensif en MP, PSI, PC, PT, MPI pendant les vacances
–> Les meilleurs professeurs de CPGE
–> Des supports pédagogiques exceptionnels
–> 100% de réussite aux concours
Avis Google France ★★★★★ 4,9 sur 5
Corrigé sur la marche de potentiel de hauteur inférieure à l’énergie.
1. Les solutions s’écrivent
* pour ![]()
![]()
![]()
* pour ![]()
![]()
![]()
2. Les particules venant de ![]() , on prend
, on prend ![]() . On écrit, en
. On écrit, en ![]() , les relations de continuité de
, les relations de continuité de ![]() et de sa dérivée car la marche de potentiel est de hauteur finie
et de sa dérivée car la marche de potentiel est de hauteur finie
![]()
![]()
En divisant la première relation par ![]() et la seconde par
et la seconde par ![]() il vient
il vient
![]() et
et ![]()
On en déduit
![]()
![]()
3. Par définition
![]()
![]()
On vérifie ![]()
4. L’énergie des deux types de particules diffère. Comme elles viennent de ![]() , où l’énergie potentielle est nulle, leur énergie est donc purement cinétique donc, en notant
, où l’énergie potentielle est nulle, leur énergie est donc purement cinétique donc, en notant ![]() leur vitesse commune
leur vitesse commune
![]() et
et ![]()
Les coefficients de transmission sont donc distincts
![]()
![]()
Sur 1 000 000 particules incidentes, 980 000 sont de masse ![]() et 20 000 de masse
et 20 000 de masse ![]()
On en déduit que dans le faisceau transmis, on en a pour celles de masse ![]() on en a
on en a
![]() de masse
de masse ![]()
![]() de masse
de masse ![]()
soient des pourcentages respectifs
97,998 de ![]() et 2,002 de
et 2,002 de ![]()
Retrouvez d’autres exercices gratuits en maths spé :
- Exercices sur la diffusion thermique en CPGE
- Exercices sur les conducteurs ohmiques en maths spé
- Exercices sur la thermochimie en prépa
- Exercices sur les référentiels non galiléens en,prépa MP, MPI, PSI, PT et PC
- Exercices en électrostatique
- Résumé de cours physique quantique en prépa

