Cours en ligne Maths en ECG1

Chapitres Maths en ECG1

Stratégie de Calcul
Espace Probabilisé
Raisonnement et Vocabulaire Ensembliste
Nombres Complexes
Polynômes
Suites Réelles
Matrices
Espaces Vectoriels et Applications Linéaires
Fonctions Réelles à Variables Réelles
Probabilités (univers infini)
Formules de Taylor et Développements Limités
Extrema et convexité
Séries Numériques
Intégration
Variables Aléatoires Finies
Variables Aléatoires Discrètes
Variables Aléatoires à Densité
Convergence et Approximations
CONTACTEZ-NOUS

Cours en ligne Maths en ECG1

Chapitres Maths en ECG1

Stratégie de Calcul
Espace Probabilisé
Raisonnement et Vocabulaire Ensembliste
Nombres Complexes
Polynômes
Suites Réelles
Matrices
Espaces Vectoriels et Applications Linéaires
Fonctions Réelles à Variables Réelles
Probabilités (univers infini)
Formules de Taylor et Développements Limités
Extrema et convexité
Séries Numériques
Intégration
Variables Aléatoires Finies
Variables Aléatoires Discrètes
Variables Aléatoires à Densité
Convergence et Approximations
CONTACTEZ-NOUS

Exercices : Stratégies de calcul en ECG1

Exercices Corrigés

Cours en ligne de Maths en ECG1

Exercices – Stratégies de calcul

Exercice 1 : 

Soient x_1, \cdots, x_n n réels tels que \sum_{k=1}^n x_k^2 = \sum_{k=1}^n x_k =n.

Montrer que pour tout k \in [\![ 1, n ]\!], x_k = 1.

 

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Professeur particulier de maths

Avis Google France ★★★★★ 4,9 sur 5

 

Exercice 2 : 

Soient x_1 , \dots , x_n et y_1, \cdots , y_n 2n réels. Le but de l’exercice est d’établir l’inégalité de Cauchy-Schwarz :

(1)   \begin{equation*} \left| \sum_{i=1}^n x_i y_i \right| \le \sqrt{\sum_{i =1}^n x_i^2 } \sqrt{\sum_{i =1}^n y_i^2 }. \end{equation*}

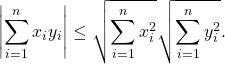
1) Montrer que l’inégalité est évidente si y_1 = \cdots = y_n = 0 .

2) On suppose dans la suite que la famille \left( y_i \right)_{i \in [\![ 1, n ]\!]} est constituée d’éléments non tous nuls. Soit f : \mathbb{R} \to \mathbb{R} définie par f \left( t \right) = \sum_{i=1}^n \left( x_i + t y_i \right)^2.    (1)

 a) Montrer que f est un trinôme du second degré en t. Préciser son signe.

   b) En calculant son discriminant \Delta, montrer (1).

Retrouvez nos cours particuliers de maths à Lyon pour progresser en stratégie de calcul en ECG1.

 

Exercice 3 : 

Si x est un réel positif, on admet qu’il existe un unique réel positif y tel que y^3 = x. Ce réel est noté \sqrt[3]{x}. La seule relation importante à retenir est le fait que y^3 =x.

Par exemple, \sqrt[3]{1000}= 10 car 10^3 = 1000.

Soit S = \sqrt[3]{45 + 29 \sqrt{2}} + \sqrt[3]{45 - 29 \sqrt{2}}.

Le but de l’exercice est de montrer que S est entier.

1) Montrer que si x, y \ge 0, alors \sqrt[3]{xy} =\sqrt[3]{x} \times \sqrt[3]{y}.

2) Vérifier que pour tout a, b \in \mathbb{R}, on a : \left( a + b \right)^3 = a^3 + 3a^2 b + 3 a b^2 + b^3.

3) En calculant S^3, vérifier que S est solution de l’équation x^3 = 21 x + 90.

4) On pose f définie sur \mathbb{R} par f \left( x \right) = x^3 - 21 x - 90. En faisant l’étude de la fonction f, montrer l’équation f \left( x \right) = 0 admet une unique solution positive x_0. En tâtonnant, montrer que cette solution est entière.

5) Conclure.

 

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

Professeur particulier maths

Avis Google France ★★★★★ 4,8 sur 5

 

Pour continuer vos révisions de maths en ECG1, révisez aussi :

Contact

Qui sommes-nous ?
Nous rejoindre
Copyright @ GROUPE REUSSITE - Mentions légales
groupe-reussite.fr est évalué 4,9/5 par 1049 clients sur Google France