Chapitres Maths en ECG1
Chapitres Maths en ECG1
Exercices : Variables aléatoires à densité en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Exercices – Variables aléatoires à densité
Exercice :
On considère une variable aléatoire ![]() suivant la loi normale centrée réduite (d’espérance nulle et de variance
suivant la loi normale centrée réduite (d’espérance nulle et de variance ![]() ) et on note
) et on note ![]() la fonction de répartition de
la fonction de répartition de ![]()
On pose ![]() et on admet que
et on admet que ![]() est une variable aléatoire. On note
est une variable aléatoire. On note ![]() la fonction de répartition de
la fonction de répartition de ![]()
1) a) Exprimer, pour tout ![]()
![]() à l’aide de
à l’aide de ![]()
b) En déduire que ![]() est une variable aléatoire à densité et donner une densité
est une variable aléatoire à densité et donner une densité ![]() de
de ![]()
c) Montrer que ![]() possède une espérance et la calculer.
possède une espérance et la calculer.
d) Montrer que ![]() possède une variance et la calculer.
possède une variance et la calculer.
2) On considère la fonction définie par :
![Rendered by QuickLaTeX.com \[g \left( x \right) = \begin{cases} \dfrac{ e^{- x} }{\sqrt{\pi x}} & \text{si} \; x> 0 \\ 0 & \text{si} \; x \le 0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ceb6ac3155fec71e36ab3538642ed5fc_l3.png)
a) Vérifier, en justifiant que l’on peut utiliser le changement de variable ![]() que :
que :
![]()
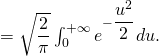
b) En déduire que ![]() est une densité.
est une densité.
3) Dans cette question, ![]() est une variable aléatoire de densité
est une variable aléatoire de densité ![]() de fonction de répartition
de fonction de répartition ![]()
a) On note ![]() et on admet que
et on admet que ![]() est une variable à densité. Exprimer la fonction de répartition
est une variable à densité. Exprimer la fonction de répartition ![]() de
de ![]() en fonction de
en fonction de ![]() puis en déduire une densité
puis en déduire une densité ![]() de
de ![]() et vérifier que
et vérifier que ![]() suit la même loi que
suit la même loi que ![]()
b) En déduire que ![]() possède une espérance et la calculer.
possède une espérance et la calculer.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
L’ensemble de nos cours en ligne de maths en ECG1 proposent aussi des exercices et corrigés sur de nombreux autres chapitres :

