Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Formules de Taylor et développements limités en ECG 1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
1. Savoir utiliser les relations de comparaison en prepa HEC ECG
Méthode 1 : La relation de négligeabilité.
![]() Pour les suites : Soient
Pour les suites : Soient ![]() et
et ![]() deux suites.
deux suites.
Si vous rencontrez des problèmes en mathématiques, nos cours particuliers de maths visent spécifiquement à assister les élèves en ECG1 dans leur démarche pour exceller en maths.
On suppose que la suite ![]() ne s’annule pas à partir d’un certain rang. Pour montrer que
ne s’annule pas à partir d’un certain rang. Pour montrer que ![]() on montre que
on montre que ![]()
![]() Pour les fonctions : Soient
Pour les fonctions : Soient ![]() et
et ![]() deux fonctions définies sur un voisinage de
deux fonctions définies sur un voisinage de ![]() (
(![]() ). On suppose que la fonction
). On suppose que la fonction ![]() ne s’annule pas au voisinage de
ne s’annule pas au voisinage de ![]() (sauf éventuellement en
(sauf éventuellement en ![]() lorsque
lorsque ![]() est réel). Pour montrer que
est réel). Pour montrer que ![]() on montre que
on montre que ![]()
Cas particuliers : on peut traduire les résultats sur les puissances comparées avec la notation « ![]() » : pour tout réel
» : pour tout réel ![]() et pour tout
et pour tout ![]()
![]()
![]()
Piège : Pour les fonctions, il faut bien indiquer le point en lequel on travaille, ici ![]() En effet, on peut très bien avoir
En effet, on peut très bien avoir
![]() et
et ![]() ainsi si l’on omet de mettre le point, il peut y avoir des ambiguïtés.
ainsi si l’on omet de mettre le point, il peut y avoir des ambiguïtés.
Par contre, pour les suites, il n’y a pas d’ambiguïté car les limites se considèrent uniquement lorsque ![]() tend vers
tend vers ![]()
Exemple : Montrer les relations de négligeabilité suivantes :
1) ![]()
2) ![]()
Réponse :
1) Le quotient ![]() donne :
donne :
![]()
Ainsi
![]()
![]()
D’où ![]()
2) On a ![]() (c’est un taux d’accroissement).
(c’est un taux d’accroissement).
D’où ![]()
Méthode 2 : La relation d’équivalence.
![]() Pour les suites : Soient
Pour les suites : Soient ![]() et
et ![]() deux suites.
deux suites.
Pour montrer que ![]() on montre qu’il existe une suite
on montre qu’il existe une suite ![]() de limite
de limite ![]() et telle que
et telle que ![]() Lorsque la suite
Lorsque la suite ![]() ne s’annule pas à partir d’un certain rang, on montre que
ne s’annule pas à partir d’un certain rang, on montre que ![]()
![]() Pour les fonctions : Soient
Pour les fonctions : Soient ![]() et
et ![]() deux fonctions définies sur un voisinage de
deux fonctions définies sur un voisinage de ![]() (
(![]() ).
).
Pour montrer que ![]() on montre qu’il existe une fonction
on montre qu’il existe une fonction ![]() définie sur un voisinage de
définie sur un voisinage de ![]() de limite
de limite ![]() et telle que
et telle que ![]()
Lorsque la fonction ![]() ne s’annule pas sur un voisinage de
ne s’annule pas sur un voisinage de ![]() sauf éventuellement en
sauf éventuellement en ![]() si
si ![]() est fini, on montre que
est fini, on montre que ![]()
Equivalents et limites : on fera attention de distinguer les résultats suivants :
![]() Si la suite
Si la suite ![]() converge vers le réel non nul
converge vers le réel non nul ![]() alors
alors ![]() Si la fonction
Si la fonction ![]() admet une limite finie non nulle
admet une limite finie non nulle ![]() en
en ![]() alors
alors ![]()
![]() Si
Si ![]() et si
et si ![]() admet une limite
admet une limite ![]() (finie ou infinie), il en est de même de la suite
(finie ou infinie), il en est de même de la suite ![]() Si
Si ![]() et si la fonction
et si la fonction ![]() admet une limite finie ou infinie
admet une limite finie ou infinie ![]() en
en ![]() il en est de même de la fonction
il en est de même de la fonction ![]()
![]() Il est utile de savoir que si
Il est utile de savoir que si ![]() avec
avec ![]() alors
alors ![]()
![]() Les équivalents « passent » bien au produit, au quotient et à la puissance, c’est-à-dire que si
Les équivalents « passent » bien au produit, au quotient et à la puissance, c’est-à-dire que si ![]() et
et ![]() alors
alors ![]()
![]() lorsque
lorsque ![]() à partir d’un certain rang.
à partir d’un certain rang.
![]() Si pour tout
Si pour tout ![]() on a
on a ![]() et
et ![]() alors pour tout
alors pour tout ![]()
![]()
![]() Si
Si ![]() si
si ![]() alors
alors ![]() (pas d’hypothèse sur le signe de
(pas d’hypothèse sur le signe de ![]() et
et ![]() ).
).
![]() Si
Si ![]() si
si ![]() et si
et si ![]() ne s’annule pas à partir d’un certain rang (il en est donc de même pour
ne s’annule pas à partir d’un certain rang (il en est donc de même pour ![]() ), alors
), alors ![]()
![]() Pour trouver un équivalent d’une somme de termes dont au moins l’un tend vers l’infini, mettre en facteur le terme qui tend le plus vite vers l’infini.
Pour trouver un équivalent d’une somme de termes dont au moins l’un tend vers l’infini, mettre en facteur le terme qui tend le plus vite vers l’infini.
![]() Pour trouver un équivalent d’une somme de termes qui admettent tous
Pour trouver un équivalent d’une somme de termes qui admettent tous ![]() pour limite, mettre en facteur le terme qui tend le moins vite vers
pour limite, mettre en facteur le terme qui tend le moins vite vers ![]()
![]() C’est une erreur classique que de penser que l’on peut composer les équivalents par la fonction l’exponentielle : si
C’est une erreur classique que de penser que l’on peut composer les équivalents par la fonction l’exponentielle : si ![]() nous n’avons pas en général
nous n’avons pas en général ![]() Pour s’en convaincre, il suffit de prendre
Pour s’en convaincre, il suffit de prendre ![]() et
et ![]()
![]() On retiendra aussi, qu’il est impossible de composer des équivalents par la fonction
On retiendra aussi, qu’il est impossible de composer des équivalents par la fonction ![]()
Par exemple, ![]() et
et ![]() sont strictement positifs, vérifient
sont strictement positifs, vérifient ![]()
Pourtant, ![]() et
et ![]()
![]() n’est donc pas équivalent à
n’est donc pas équivalent à ![]()
Quelques équivalents usuels à retenir :
![]()
Exemple : 1) Montrer la relation d’équivalence suivante :
![]()
2) Trouver un équivalent de : ![]() en
en ![]() et en
et en ![]()
Réponse :
1) Si l’on pose ![]()
![]() est dérivable en
est dérivable en ![]() et
et ![]()
![]()
![]()
![]() donc
donc ![]()
![]() soit
soit ![]()
2) En ![]() :
:
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Formules de Taylor en prepa HEC ECG
Méthode 3 : Appliquer l’inégalité de Taylor-Lagrange.
Soit ![]() une fonction de classe
une fonction de classe ![]() sur un intervalle
sur un intervalle ![]() telle que
telle que ![]() soit bornée sur
soit bornée sur ![]() Soient
Soient ![]() et
et ![]() deux points de
deux points de ![]() alors :
alors :
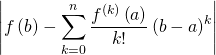
![]()
Remarque : lorsque l’on ne suppose pas ![]() bornée sur
bornée sur ![]() on peut quand même écrire : pour tout
on peut quand même écrire : pour tout ![]()
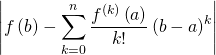
![]()
Cette formule servira dans les cas suivants :
![]() lorsque l’on doit montrer des inégalités faisant intervenir les dérivées successives d’une fonction,
lorsque l’on doit montrer des inégalités faisant intervenir les dérivées successives d’une fonction,
![]() et dans les exercices plus théoriques faisant intervenir des dérivées successives en un même point (c’est vague, je sais…).
et dans les exercices plus théoriques faisant intervenir des dérivées successives en un même point (c’est vague, je sais…).
Exemple :Montrer que tout réel ![]() on a
on a
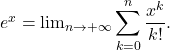
Réponse : Il suffit d’écrire l’inégalité de Taylor-Lagrange avec
![]()
en remarquant que pour tout ![]()
![]() et
et ![]()
Si ![]()
![]() et si
et si ![]()
![]() Dans tous les cas,
Dans tous les cas, ![]()
![]() D’où :
D’où :
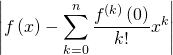
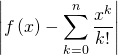
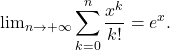
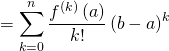
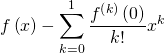
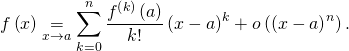
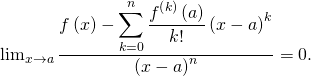
Puis,
Remarque : Et maintenant la question que vous vous posez, quelle formule de Taylor choisir ?![]() Vous cherchez une propriété valable au voisinage d’un point
Vous cherchez une propriété valable au voisinage d’un point ![]() (ce que l’on appelle une propriété locale) : pensez à la formule de Taylor-Young.
(ce que l’on appelle une propriété locale) : pensez à la formule de Taylor-Young.
![]() Vous cherchez une propriété valable sur tout un intervalle (ce que l’on appelle une propriété globale) :
Vous cherchez une propriété valable sur tout un intervalle (ce que l’on appelle une propriété globale) :
![]() elle contient une valeur absolue ; pensez inégalité de Taylor-Lagrange,
elle contient une valeur absolue ; pensez inégalité de Taylor-Lagrange,
![]() il n’y a pas de valeur absolue : vous avez la malchance de devoir vous souvenir de la formule de Taylor avec reste intégral, mais rassurez-vous, la situation est rare.
il n’y a pas de valeur absolue : vous avez la malchance de devoir vous souvenir de la formule de Taylor avec reste intégral, mais rassurez-vous, la situation est rare.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
3. Développements limités en prepa ECG
Méthode 6 : Savoir faire un développement limité.
On donne ci-dessous la liste des développements limités usuels au voisinage de ![]() Il faut absolument la connaître sur le bout des doigts.
Il faut absolument la connaître sur le bout des doigts.

On rappelle que ces développements limités sont une conséquence de la formule de Taylor-Young : si ![]() est une fonction de classe
est une fonction de classe ![]() au voisinage d’un point
au voisinage d’un point ![]() alors
alors ![]() admet un développement limité à l’ordre
admet un développement limité à l’ordre ![]() en
en ![]() et :
et :
![]()
![]()
![]()
Les développements limités servent principalement à :
![]() calculer des limites (lorsqu’il y a des formes indéterminées),
calculer des limites (lorsqu’il y a des formes indéterminées),
![]() faire l’étude de fonction au voisinage d’un point (continuité, dérivabilité, signe, etc.),
faire l’étude de fonction au voisinage d’un point (continuité, dérivabilité, signe, etc.),
![]() trouver un équivalent simple dans le cas d’une somme de fonctions. On retiendra que c’est le premier terme non nul du développement limité.
trouver un équivalent simple dans le cas d’une somme de fonctions. On retiendra que c’est le premier terme non nul du développement limité.
Remarque : ![]() le choix de l’ordre d’un développement limité pour lever une forme indéterminée est crucial : il doit être assez élevé pour lever l’indétermination mais pas trop pour éviter de faire trop de calculs,
le choix de l’ordre d’un développement limité pour lever une forme indéterminée est crucial : il doit être assez élevé pour lever l’indétermination mais pas trop pour éviter de faire trop de calculs,
![]() lorsque l’on demande un développement limité en
lorsque l’on demande un développement limité en ![]() la méthode la plus simple est de faire le changement de variable
la méthode la plus simple est de faire le changement de variable ![]() avec
avec ![]() quand
quand ![]() et de faire un développement limité en
et de faire un développement limité en ![]() en fonction des puissances de
en fonction des puissances de ![]() puis d’exprimer le résultat en fonction des puissances de
puis d’exprimer le résultat en fonction des puissances de ![]() sans les développer.
sans les développer.
Exemple : Calculer les développements limités à l’ordre et au point indiqué pour les fonctions suivantes :
1) ![]() en
en ![]() à l’ordre
à l’ordre ![]()
2) ![]() en
en ![]() à l’ordre
à l’ordre ![]()
Réponse : 1) Sachant que l’on doit diviser le développement de ![]() par
par ![]() pour obtenir le développement limité à l’ordre
pour obtenir le développement limité à l’ordre ![]() il faut écrire celui de
il faut écrire celui de ![]() à l’ordre
à l’ordre ![]() donc celui de
donc celui de ![]() à l’ordre
à l’ordre ![]()
Le développement limité de ![]() en
en ![]() à l’ordre
à l’ordre ![]() donne :
donne :
![]()
![]()
2) Le développement limité demandé n’est pas au voisinage de ![]() On pose
On pose ![]() de sorte que lorsque
de sorte que lorsque ![]()
![]() On a :
On a :
![]()
puis en remplaçant ![]() par
par ![]() on a :
on a :
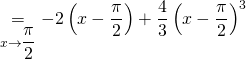
évidemment, on ne développe pas !D’autres chapitres au programme de maths en ECG1 peuvent également être travaillés grâce à nos cours en ligne :

