Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Matrices en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Matrices inversibles, produit de matrices & polynôme d’une matrice
Méthode 1 : Produit de matrices.
Rappelons que la notation ![]() désigne l’ensemble des matrices à coefficients dans
désigne l’ensemble des matrices à coefficients dans ![]() ayant
ayant ![]() lignes et
lignes et ![]() colonnes.
colonnes.
Dans le cas où ![]() on identifie
on identifie ![]() avec
avec ![]()
Soient ![]() et
et ![]() deux matrices. Pour que le produit
deux matrices. Pour que le produit ![]() ait un sens, il faut et il suffit que
ait un sens, il faut et il suffit que ![]() Dans ce cas,
Dans ce cas, ![]()
Dans le cas particulier où ![]() et
et ![]() sont deux matrices carrées d’ordre
sont deux matrices carrées d’ordre ![]() le produit
le produit ![]() est défini et est une matrice carrée d’ordre
est défini et est une matrice carrée d’ordre ![]()
Il faut donc retenir que :
![]() le produit
le produit ![]() est donc possible si et seulement si le nombre de colonnes de
est donc possible si et seulement si le nombre de colonnes de ![]() est égal au nombre de lignes de
est égal au nombre de lignes de ![]()
![]() si
si ![]() et
et ![]()
alors ![]() o\`u si
o\`u si ![]() et
et ![]() on a
on a
![Rendered by QuickLaTeX.com \[c_{i, j} = \sum_{k=1}^p a_{i,k} b_{k , j} .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e8e73a8051b17e43dd34f8e29461ca51_l3.png)
![]() dans le cas particulier où
dans le cas particulier où ![]() est une matrice colonne
est une matrice colonne ![]() alors le produit
alors le produit ![]() est une matrice colonne dont le nombre de lignes est égal au nombre de lignes de
est une matrice colonne dont le nombre de lignes est égal au nombre de lignes de ![]()
Si ![]() et
et 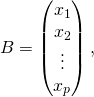 alors
alors ![]() avec, pour
avec, pour ![]()
![Rendered by QuickLaTeX.com \[y_i = \sum_{k=1}^p a_{i , k} x_k.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b7160d47e8ba9494d41acbe0cbdbc8b5_l3.png)
Exemple : On pose 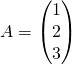 et
et ![]()
Calculer les matrices ![]() et
et ![]() si cela est possible.
si cela est possible.
Réponse :
![]() Le nombre de colonnes de
Le nombre de colonnes de ![]() est égal au nombre de lignes de
est égal au nombre de lignes de ![]() donc le produit
donc le produit ![]() existe et
existe et
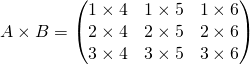
= 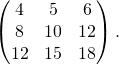
![]() Le nombre de colonnes de
Le nombre de colonnes de ![]() est égal au nombre de lignes de
est égal au nombre de lignes de ![]() donc le produit
donc le produit ![]() existe et
existe et
![]()
Découvrez nos cours de maths à Paris sur notre plateforme dédiée à votre succès scolaire en ECG1.
Méthode 2 : Polynôme d’une matrice.
![]() Si
Si ![]() et si
et si ![]() on définit la matrice
on définit la matrice
![]()
![]()
![]() On peut montrer que si
On peut montrer que si ![]() et si
et si ![]()
![]()
![]() On dit que
On dit que ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]() si
si ![]() On remarque que le polynôme nul annule toutes les matrices, ce n’est donc pas un polynôme annulateur très intéressant !
On remarque que le polynôme nul annule toutes les matrices, ce n’est donc pas un polynôme annulateur très intéressant !
![]() A ce sujet pour une matrice
A ce sujet pour une matrice ![]() avez-vous remarqué que
avez-vous remarqué que
![]()
Cela signifie que ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]()
Exemple : Soit ![]() Soit
Soit ![]() calculer
calculer ![]()
Réponse : Par définition, on a :
![]()
![]()
![]()
Méthode 3 : Calcul de puissances de matrices.
Il faut se souvenir que calculer la puissance ![]() -ième d’une matrice, ce n’est -presque- jamais simple! Il y a des cas où l’on sait faire :
-ième d’une matrice, ce n’est -presque- jamais simple! Il y a des cas où l’on sait faire :
![]() si
si ![]() est diagonale, alors
est diagonale, alors ![]()
![]() si
si ![]() est nilpotente (i.e. il existe
est nilpotente (i.e. il existe ![]() tel que
tel que ![]() ) alors, pour tout
) alors, pour tout ![]() on a
on a ![]() Il reste simplement à calculer
Il reste simplement à calculer ![]()
On peut quand même donner quelques méthodes générales pour s’en sortir.
![]() Dans le cas où
Dans le cas où ![]() avec
avec ![]() on peut utiliser la formule du binôme de Newton.
on peut utiliser la formule du binôme de Newton.
Cette méthode marchera bien si ![]() et si les puissances de
et si les puissances de ![]() sont simples à calculer (par exemple
sont simples à calculer (par exemple ![]() nilpotente).
nilpotente).
![]() Essayer de conjecturer une formule puis la montrer par récurrence.
Essayer de conjecturer une formule puis la montrer par récurrence.
![]() Si l’on a un polynôme annulateur
Si l’on a un polynôme annulateur ![]() de la matrice
de la matrice ![]() on peut faire la division euclidienne de
on peut faire la division euclidienne de ![]() par
par ![]() cela donne
cela donne ![]() avec
avec ![]() Cette relation donne
Cette relation donne ![]() car
car ![]()
Cette méthode est très efficace surtout si l’on connaît un polynôme annulateur de ![]() de petit degré (
de petit degré (![]() ou
ou ![]() ).
).
Exemple : Calculer leur puissance ![]() -ième de
-ième de 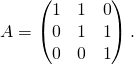
Réponse :
Ecrivons ![]() avec
avec ![]() la matrice identité et
la matrice identité et 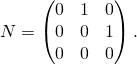 On remarque que
On remarque que 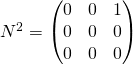 et
et ![]() Ainsi pour
Ainsi pour ![]() , en appliquant la formule du binôme de Newton (possible car
, en appliquant la formule du binôme de Newton (possible car ![]() et
et ![]() commutent), on a
commutent), on a
![]()
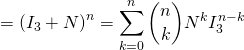
![]()
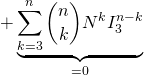
![]() .
.
Pour ![]() on a
on a ![]() pour
pour ![]() la relation trouvée ci-dessus est donc vraie pour tout entier
la relation trouvée ci-dessus est donc vraie pour tout entier ![]()
Méthode 4 : Appliquer l’algorithme du pivot de Gauss.
Il est fondamental de savoir résoudre de fa\c{c}on efficace un système d’équations, c’est un passage obligé en mathématiques et malheureusement rébarbatif. C’est grâce à cela que l’on peut inverser des matrices. Il est important de savoir le faire et sans erreur de calculs !
Le point de départ est le système suivant (pas nécessairement carré bien qu’en pratique, ils le sont tous !) avec pour inconnues ![]() les autres coefficients
les autres coefficients ![]() et
et ![]() sont supposés connus.
sont supposés connus.
![Rendered by QuickLaTeX.com \[\begin{cases} a_{1,1} x_1 + a_{1,2 } x_2 + \cdots + a_{1, n} x_n & = b_1 \\ a_{2,1} x_1 + a_{2,2 } x_2 + \cdots + a_{2, n} x_n & = b_2 \\ \vdots \\ a_{m,1} x_1 + a_{m,2 } x_2 + \cdots + a_{m, n} x_n & = b_m \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-302274689cb13f0c8ac84ba0119d85a2_l3.png)
On suppose que l’un des coefficients ![]() pour
pour ![]() est non nul. En changeant éventuellement l’ordre des équations, on peut se ramener au cas o\`u
est non nul. En changeant éventuellement l’ordre des équations, on peut se ramener au cas o\`u ![]() On dit que
On dit que ![]() est le premier pivot. En pratique, on choisit un pivot simple, égal à
est le premier pivot. En pratique, on choisit un pivot simple, égal à ![]() lorsque c’est possible.
lorsque c’est possible.
En faisant des opérations sur les lignes (c’est-à-dire que l’on fait ![]() avec
avec ![]() ), il faut réussir à annuler les coefficients devant
), il faut réussir à annuler les coefficients devant ![]() à partir de la deuxième ligne. Comme
à partir de la deuxième ligne. Comme ![]() on utilise
on utilise ![]() pour tout
pour tout ![]() de sorte que le système devienne :
de sorte que le système devienne :
![Rendered by QuickLaTeX.com \[\begin{cases} a_{1,1} x_1 + a_{1,2 } x_2 + \cdots + a_{1, n} x_n & = b_1 \\ \qquad \quad \ \ \widetilde{a_{2,2 }} x_2 + \cdots + \widetilde{a_{2, n}} x_n & = \widetilde{b_2} \\ \qquad \quad \ \ \vdots \\ \qquad \quad \ \ \widetilde{ a_{m,2 } } x_2 + \cdots + \widetilde{a_{m, n} } x_n & =\widetilde{ b_m} \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a3b412523ac102a8a54954d3292a9808_l3.png)
Si tous les coefficients ![]() pour
pour ![]() et
et ![]() sont nuls, alors les opérations de triangularisation du système sont terminées.
sont nuls, alors les opérations de triangularisation du système sont terminées.
Si au moins l’un des coefficients ![]() pour
pour ![]() et
et ![]() est non nul, on introduit en changeant éventuellement l’ordre des équations
est non nul, on introduit en changeant éventuellement l’ordre des équations ![]() \`a
\`a ![]() le pivot suivant de deuxième indice
le pivot suivant de deuxième indice ![]() minimum. En changeant éventuellement l’ordre des équations, on suppose que c’est le coefficient de
minimum. En changeant éventuellement l’ordre des équations, on suppose que c’est le coefficient de ![]() dans la ligne
dans la ligne ![]() On obtient un système du type :
On obtient un système du type :
![Rendered by QuickLaTeX.com \[\begin{cases} a_{1,1} x_1 + \cdots + a_{1, n } x_n \qquad \quad \ \ \qquad \quad \ \ \qquad \quad \ \ \qquad \quad \ \ & = b_1 \\ \qquad \quad \ \ \widetilde{a_{2,j}} x_j + \cdots + \widetilde{a_{2 , n}} x_n \qquad \ \ \qquad \quad \ \ \qquad \ \ \qquad & = \widetilde{b_2} \\ \qquad \quad \ \ \qquad \quad \ \ \widetilde{a_{3,j}} x_j + \cdots + \widetilde{a_{3 , n}} x_n \qquad \qquad \qquad \; \; \; \; \; & = \widetilde{b_3} \\ \qquad \qquad \qquad \qquad \qquad \ddots \\ \qquad \quad \ \ \qquad \quad \qquad \quad \ \ \qquad \quad \ \ \widetilde{a_{m,j}} x_j + \cdots + \widetilde{a_{m , n}} x_n \, & = \; \widetilde{b_m} \end{cases},\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f271d28b2a5aa68bfffa02eb2e2cf9ab_l3.png)
avec ![]()
Attention : on ne touche pas à la première ligne dans cette phase de l’algorithme.
Pour les lignes ![]() à
à ![]() on effectue l’opération
on effectue l’opération ![]() de fa\c{c}on à faire disparaître le coefficient de
de fa\c{c}on à faire disparaître le coefficient de ![]() dans les lignes numérotées de
dans les lignes numérotées de ![]() à
à ![]()
On poursuit la méthode précédente sur les lignes ![]() à
à ![]() jusqu’à ne plus trouver de pivot. On obtient à la fin un système triangulaire que l’on résout en commençant par la dernière équation.
jusqu’à ne plus trouver de pivot. On obtient à la fin un système triangulaire que l’on résout en commençant par la dernière équation.
Il est possible d’obtenir un système sans solution, avec une infinité de solutions, et dans le cas ![]() une unique solution.
une unique solution.
Exemple : Résoudre le système suivant en discutant suivant le paramètre ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases} \left( 1 - m \right) x + 2 y - z & = 0 \\ 2 x + \left( 2 - m \right) y + 2 z & = 1 \\ x - 2 y + 3 z & = 2 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-db6ecfbaa0644650c8336676da5ec8d3_l3.png)
Réponse :
On ne choisit pas ![]() comme pivot (car il s’annule pour
comme pivot (car il s’annule pour ![]() ). On va échanger les lignes
). On va échanger les lignes ![]() et
et ![]() le système devient donc :
le système devient donc :
![Rendered by QuickLaTeX.com \[\begin{cases} x - 2y + 3 z & = 2 \\ 2 x + \left( 2 - m \right) y + 2 z & = 1 \\ \left( 1 - m \right) x + 2 y - z & = 0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-66caaba95438a8477bedb7c188a5f6d1_l3.png)
En utilisant ![]() et
et ![]() on obtient le système suivant :
on obtient le système suivant :
![Rendered by QuickLaTeX.com \[\begin{cases} x - 2y + 3z & = 2 \\ \left( 6 - m \right) y - 4 z & = - 3 \\ \left( 4 - 2m \right) y + \left( 3m- 4 \right) z & = 2 \left( m - 1 \right) \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-eeb7c530e0d637e26ae8823d08e09ae8_l3.png)
Les deux coefficients de ![]() dans les deux dernières lignes s’annulant, on place l’inconnue
dans les deux dernières lignes s’annulant, on place l’inconnue ![]() en deuxième position ce qui permet d’avoir un pivot égal à
en deuxième position ce qui permet d’avoir un pivot égal à ![]() indépendant de
indépendant de ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases} x + 3 z - 2 y & = 2 \\ - 4 z + \left( 6 - m \right) y & = - 3 \\ \left( 3 m - 4 \right) z + \left( 4 - 2 m \right) y & = 2 \left( m - 1 \right) \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2ada0dafdc6c3ade14475d1e90da7f35_l3.png)
Avec l’opération ![]() et après avoir multiplié de
et après avoir multiplié de ![]() par
par ![]() on obtient :
on obtient :
![Rendered by QuickLaTeX.com \[\begin{cases} x + 3 z - 2 y & = 2 \\ - 4 z + \left( 6 - m \right) y & = - 3 \\ - \left( 3m^2 - 14 m + 8 \right) y & = - \left( m - 4 \right) \end{cases},\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ffd1f5c50476b57823d2a76c7a40013e_l3.png)
soit
![Rendered by QuickLaTeX.com \[\begin{cases} x + 3 z - 2 y & = 2 \\ - 4 z + \left( 6 - m \right) y & = - 3 \\ \left( 3m - 2 \right) \left( m - 4 \right) y & = m - 4 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2faa4c7a968aafae42126bd3280a3728_l3.png)
![]() Dans le cas où
Dans le cas où ![]() on résout la dernière équation qui donne la valeur de
on résout la dernière équation qui donne la valeur de ![]() puis avec la deuxième ligne, on obtient
puis avec la deuxième ligne, on obtient ![]() et avec la première ligne, on obtient la valeur de
et avec la première ligne, on obtient la valeur de ![]() soit :
soit :
![]()
Le système admet une unique solution : ![]()
![]() Si
Si ![]() la dernière ligne s’écrit
la dernière ligne s’écrit ![]() elle est impossible, le système n’a pas de solution.
elle est impossible, le système n’a pas de solution.
![]() Si
Si ![]() le système s’écrit (puisque la dernière équation est
le système s’écrit (puisque la dernière équation est ![]() ) :
) :
![Rendered by QuickLaTeX.com \[\begin{cases} x + 3 z - 2y & = 2 \\ - 4 z + 2 y & = - 3 \end{cases},\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9d2dd59f6ab3430c1281cde026211713_l3.png)
soit encore
![Rendered by QuickLaTeX.com \[\begin{cases} x + 3 z - 2y & = 2 \\ y & = - \dfrac32 + 2z \end{cases} \Leftrightarrow \begin{cases}x & = - 3 z + 2y + 2 \\ y & = - \dfrac32 + 2z \end{cases} \Leftrightarrow \begin{cases}x & = z - 1 \\ y & =2z - \dfrac32 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1c815a2fd7a427a530931a2587de2901_l3.png)
Le système admet une infinité de solutions ![]()
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Méthode 5 : Montrer qu’une matrice est inversible et calculer son inverse.
On rappelle que la matrice carrée d’ordre ![]() est dite inversible s’il existe une matrice
est dite inversible s’il existe une matrice ![]() telle que
telle que ![]() La matrice
La matrice ![]() est alors unique et on la note
est alors unique et on la note ![]()
On sait que s’il existe une matrice carrée de même ordre ![]() que
que ![]() telle que
telle que ![]() ou telle que
ou telle que ![]() alors
alors ![]() est inversible et
est inversible et ![]()
On rappelle aussi qu’une matrice diagonale ou triangulaire ![]() est inversible si, et seulement si, le produit des termes diagonaux est non nul.
est inversible si, et seulement si, le produit des termes diagonaux est non nul.
Voici diverses méthodes pour montrer qu’une matrice carrée ![]() d’ordre
d’ordre ![]() est inversible et calculer son inverse :
est inversible et calculer son inverse :
![]() On peut résoudre le système
On peut résoudre le système ![]() c’est-à-dire étant donnée une matrice colonne
c’est-à-dire étant donnée une matrice colonne ![]() arbitraire à
arbitraire à ![]() lignes, existe t-il
lignes, existe t-il ![]() unique de type
unique de type ![]() telle que
telle que ![]() ? Si oui,
? Si oui, ![]() est inversible, sinon elle ne l’est pas. Lorsqu’elle est inversible, on obtient
est inversible, sinon elle ne l’est pas. Lorsqu’elle est inversible, on obtient ![]() en exprimant
en exprimant ![]() en fonction de
en fonction de ![]()
![]() Si l’on a un polynôme annulateur de
Si l’on a un polynôme annulateur de ![]() de terme constant
de terme constant ![]() on peut isoler
on peut isoler ![]() et factoriser par
et factoriser par ![]() le reste de l’expression pour faire apparaître une relation du type
le reste de l’expression pour faire apparaître une relation du type ![]() (ou
(ou ![]() ) et pour conclure que
) et pour conclure que ![]() est inversible d’inverse
est inversible d’inverse ![]()
Exemple : Montrer que la matrice 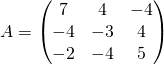 est inversible et calculer son inverse.
est inversible et calculer son inverse.
Réponse :
On vérifie facilement que ![]() (faites-le !). Ainsi, en « passant »
(faites-le !). Ainsi, en « passant » ![]() à droite de l’égalité, on a
à droite de l’égalité, on a
![]()
puis, sans oublier la matrice ![]() apr\`es
apr\`es ![]() (c’est une faute courante, il ne faut pas la faire !) :
(c’est une faute courante, il ne faut pas la faire !) :
![]()
Cela prouve que ![]() est inversible et
est inversible et ![]() Après calculs, on a
Après calculs, on a
![Rendered by QuickLaTeX.com \[A^{- 1} = \dfrac{1}{15} \begin{pmatrix} 1 & 4 & - 4 \\ 12 & 27 & -12 \\ 10 & 20 & - 5 \end{pmatrix}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c0dff53a40801b384bc273dab88b7352_l3.png)
Méthode 6 : Montrer qu’une matrice n’est pas inversible.
Pour montrer qu’une matrice n’est pas inversible, on peut essayer de trouver une combinaison linéaire non triviale entre les colonnes donnant ![]() Plus précisément, si
Plus précisément, si ![]() est une matrice de taille
est une matrice de taille ![]() dont les colonnes sont notées
dont les colonnes sont notées ![]() et si l’on trouve
et si l’on trouve ![]() non tous nuls tels que
non tous nuls tels que
![]()
alors la matrice ![]() n’est pas inversible et si
n’est pas inversible et si 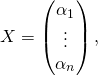 alors
alors ![]()
Si l’on ne trouve pas « à vu » les réels ![]() pour montrer que la matrice
pour montrer que la matrice ![]() n’est pas inversible, on montre que le système
n’est pas inversible, on montre que le système ![]() admet au moins une solution non nulle.
admet au moins une solution non nulle.
Exemple : Montrer que la matrice 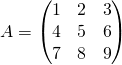 n’est pas inversible.
n’est pas inversible.
Réponse :
On pose 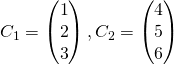 et
et 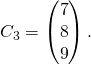 On remarque que
On remarque que ![]() ainsi
ainsi ![]() n’est pas inversible, dit autrement (c’est équivalent)
n’est pas inversible, dit autrement (c’est équivalent)
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \begin{pmatrix} 1 \\ - 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-db2554d07e24cf42b43174710c36230a_l3.png)
Si l’on ne devine pas la relation ![]() on peut chercher
on peut chercher ![]() et
et ![]() non tous nuls tels que
non tous nuls tels que ![]() soit résoudre le système :
soit résoudre le système :
![Rendered by QuickLaTeX.com \[\begin{cases} x + 2 y + 3 z & = 0 \\ 4 x + 5 y + 6 z & = 0 \\ 7 x + 8 y + 9 z & =0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d9357902a1cb3e03a3d3da5fbd308cac_l3.png)
En utilisant ![]() et
et ![]()
![Rendered by QuickLaTeX.com \[\begin{cases} x + 2 y + 3 z & = 0 \\ - 3 y - 6 z & = 0 \\ - 6 y - 12 z & =0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2f919ecdb39aa495fed05c258349c810_l3.png)
Et enfin, puisque la troisième équation est le double de la deuxième, on a
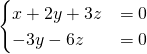
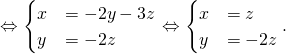
On retrouve l’égalité ![]() en prenant
en prenant ![]()
Regardez dès maintenant tous les autres cours en ligne de maths en ECG1 pour être sûr d’avoir bien assimilé toutes les notions de cours :

