Cours en ligne Physique-Chimie en Maths Spé

Chapitres Physique-Chimie en MP, PSI, PC, MPI, TSI, PT

Cours sur ondes électromagnétiques dans le vide en MP, PC, MPI, PSI, PT

L’investissement de temps dans l’étude du cours des ondes électromagnétiques en physique chimie est essentiel pour les étudiants en maths spé, car cette matière joue un rôle primordial dans leur programme. On va revoir quelques concepts de physique chimie : Solution OPPH PR, ondes stationnaires, ondes guidées, polarisation rectiligne et rayonnement du dipôle oscillant La prise de cours de soutien en CPGE avec des professeurs particuliers en physique chimie peut également être avantageuse pour les blocages en physique chimie.

Équation de Maxwell et d’Alembert : propagation ondes dans le vide

Méthode 1 : écriture des équations de Maxwell dans le vide.

Dans le vide de charge $\rho=0$ et de courants $\vec{j}=\vec{0}$

On en déduit les équations de Maxwell-Gauss et de Maxwell-Thomson

$\mathrm{div}\vec{E}=0$ et $\mathrm{div}\vec{B}=0$

Les équations de Maxwell-Faraday et de Maxwell-Ampère

$\displaystyle{\vec{\mathrm{rot}}\vec{E}=-\frac{\partial \vec{B}}{\partial t}}$ et

$\displaystyle{\vec{\mathrm{rot}}\vec{B}=\varepsilon_0\mu_0\frac{\partial \vec{E}}{\partial t}}$

Méthode 2 : établissement de l’équation de d’Alembert

On utilise

1. La relation d’analyse vectorielle

$\vec{\mathrm{rot}}\vec{\mathrm{rot}}\vec{A}=\vec{\mathrm{grad}}\mathrm{div}\vec{A}-\Delta\vec{A}$

2. Le théorème de Schwartz qui permet de permuter un opérateur de dérivation spatial et l’opérateur de dérivation temporelle.

On en déduit que $\vec{E}$ et $\vec{B}$ vérifient la même équation de d’Alembert

$\displaystyle{\Delta\vec{E}-\frac1{c_0^2}\frac{\partial^2\vec{E}}{\partial t^2}=\vec{0}}$

$\displaystyle{\Delta\vec{B}-\frac1{c_0^2}\frac{\partial^2\vec{B}}{\partial t^2}=\vec{0}}$

avec $\displaystyle{c_0=\frac1{\sqrt{\varepsilon_0\mu_0}}=3,00\cdot 10^8~\mathrm{m\cdot s^{-1}}}$

Exemple.

Établir l’EDA pour $\vec{E}$

COURS DE PHYSIQUE

Trouvez le professeur parfait de physique

Là pour vous guider, quel que soit votre niveau scolaire

Avis Google France ★★★★★ 4,9 sur 5

Solution OPPH PR en MP, PC, PSI, MPI

Méthode 1 : expliciter la solution OPPH PR en grandeurs réelles.

La solution Onde Plane Progressive Harmonique Polarisée Rectilignement s’écrit, pour le champ électrique

$\displaystyle{\vec{E}=E_0\vec{u}_x\cos\left(\omega t-kx+\varphi\right)}$

Son vecteur d’onde est $\vec{k}=k\vec{u}_x$

La relation de dispersion s’écrit $\displaystyle{\omega=kc_0}$

Elle est polarisée selon $\vec{u}_x$

Le champ magnétique vibre en phase avec le champ électrique

$\displaystyle{\vec{B}=B_0\vec{u}_y\cos\left(\omega t-kx+\varphi\right)}$

avec $\displaystyle{E_0=c_0B_0}$

$\displaystyle{\left(\vec{k},\vec{E},\vec{B}\right)}$ forme un trièdre orthogonal direct

La relation de structure s’écrit

$\displaystyle{\vec{B}=\frac{\vec{k}\wedge\vec{E}}{\omega}}$

Exemple.

1. Vérifier la transversalité de l’onde.

2. Vérifier la relation de dispersion.

Méthode 2 : expliciter la solution OPPH PR en grandeurs complexes.

On écrit

$\displaystyle{\vec{\underline{E}}=\vec{\underline{E}}_0\exp\left(i(\omega t-\vec{k}\cdot\vec{OM})\right)}$

En grandeurs complexes

$\displaystyle{\mathrm{div}\vec{\underline{A}}=-i\vec{k}\cdot\vec{\underline{A}}}$

$\displaystyle{\vec{\mathrm{rot}}\vec{\underline{A}}=-i\vec{k}\wedge\vec{\underline{A}}}$

En injectant dans les équations de Maxwell, on en déduit

* la transversalité des champs électrique et magnétique

* la relation de structure

* la relation de dispersion.

Exemple.

Démontrer la relation de structure en grandeurs complexes.

Méthode 3 : expliciter les propriétés énergétiques de l’OPPH.

Le vecteur de Poynting vaut

$\displaystyle{\vec{\Pi}=\frac{\vec{E}\wedge\vec{B}}{\mu_0}=\frac{E_0^2}{\mu_0c_0}\vec{u}_z\cos^2\left(\omega t-kx+\varphi\right)}$

Il a la direction et le sens de propagation de l’onde électromagnétique dans le vide.

Sa valeur moyenne dans le temps vaut

$\displaystyle{<\vec{\Pi}>=\frac{E_0^2}{2\mu_0c_0}\vec{u}_z}$

Il est exprimé en joules par mètre carré et par seconde. Son flux est égal à la puissance traversant la surface considérée.

Exemple.

Donner la valeur moyenne du vecteur de Poynting en fonction de $B_0$ et indépendamment de $E_0$

Ondes stationnaires, ondes guidées : ondes électromagnétiques vide

Méthode 1 : conditions aux limites pour les OEM

La présence de plaques métalliques conductrices parfaites impose des CL.

Le champ électrique est nul dans ces plaques.

La composante tangentielle du champ électrique est toujours continue.

S’il y a nullité des charges surfaciques, il y a continuité complète du champ électrique.

La composante normale du champ magnétique est toujours continue.

S’il y a nullité des courants surfaciques, il y a continuité complète du champ magnétique.

Exemple.

Montrer que le champ électrique à la surface d’une plaque parfaitement conductrice vaut

$\displaystyle{\vec{E}=\frac{\sigma}{\varepsilon_0}\vec{n}}$

avec $\sigma$ densité surfacique de charge et $\vec{n}$ vecteur normal dirigé de la plaque vers l’extérieur.

Méthode 2 : expliciter l’onde stationnaire entre deux plaques.

On cherche une solution de l’EDA dans le vide entre deux plaques parallèles métalliques parfaitement conductrices en $z=0$ et en $z=a$ sous la forme d’une onde stationnaire, produit d’une fonction de l’espace par une fonction du temps

$\displaystyle{\vec{E}(z,t)=E_0\vec{u}_xu(t)g(z)}$

On établit par séparation des variables que l’onde stationnaire est nécessairement harmonique

$\displaystyle{\vec{E}(z,t)=E_0\vec{u}_x\cos(\omega t+\varphi)\cos(kx+\psi)}$

avec la même relation de dispersion que pour la solution progressive $\omega=kc_0$

Il y a quantification de la pulsation temporelle $\omega$ et de la pulsation spatiale $k$ , en particulier

$\displaystyle{a=n\frac{\lambda}{2}}$ avec $n$ entier naturel non nul.

Exemple.

Donner les expressions de $\psi$ et de $k$ cohérentes avec les CL

Méthode 3 : étudier une solution du type propagation guidée

Entre deux plaques parallèles métalliques parfaitement conductrices, ou entre les armatures cylindriques d’une ligne coaxiale, on peut chercher une solution du type onde guidée.

1. On injecte la solution proposée dans les équations de Maxwell. Attention ! le formalisme complexe n’est en général pas adapté car ce n’est pas une OPPH.

2. On injecte la solution proposée dans l’EDA et on en déduit après simplification une équation différentielle qu’on résout en prenant en compte les CL imposées par les plaques métalliques.

3. On en déduit les ondes électrique et magnétique, puis le vecteur de Poynting.

4. En calculant le flux du vecteur de Poynting à travers une surface de référence, on en déduit l’énergie transportée par l’onde.

Exemple.

Entre les plaques métalliques parfaitement conductrices $y=0$ et $y=a$ on cherche une OEM sous la forme

$\displaystyle{\vec{E}=E_0\vec{u}_xf(x)\cos(\omega t)\cos(kz)}$

Quelle est l’équation différentielle vérifiée par $f(x)$ ?

PRENDRE DES COURS DE PHYSIQUE CHIMIE

C’est comprendre et réussir

Polarisation rectiligne

Méthode 1 : identifier mathématiquement une onde polarisée rectilignement.

L’OPPH PR peut être difficile à identifier dans une base cartésienne quelconque.

1. Pour savoir si une onde est polarisée rectilignement (PR), on doit vérifier que la direction du champ électrique est constante.

2. On peut alors écrire

$\vec{E}(M,t)=\vec{E}_0\cos(\omega t-\vec{k}\cdot\vec{OM}+\varphi)$

et on en déduit $\vec{k}$

2. Pour vérifier que l’onde est transverse, on doit vérifier $\mathrm{div}\vec{E}=0$ ou $\vec{k}\cdot\vec{E}=0$

Exemple.

L’onde 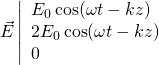$\displaystyle{\vec{E}\left|\begin{array}{l} E_0\cos(\omega t-kz) \\ 2E_0\cos(\omega t-kz) \\ 0 \end{array}\right.}$

est-elle plane ? polarisée rectilignement ? transverse ?

Méthode 2 : former une quasi OPPH PR au laboratoire

1. Le H de l’acronyme signifie « harmonique », l’onde doit donc être monochromatique, on peut donc sélectionner une longueur d’onde d’une lampe spectrale, par exemple grâce à un prisme ou à un filtre interférométrique de Fabry-Perot (celui qu’on utilise pour la raie verte du mercure). On obtient ainsi une onde quasi monochromatique.

2. On forme ensuite une source quasi-ponctuelle en concentrant la lumière vers un diaphragme grâce à un condenseur.

3. On place ensuite le diaphragme au foyer objet d’une lentille CV et on obtient un faisceau quasi cylindrique de lumière quasi-monochromatique, le vecteur d’onde est $\vec{k}=k\vec{u}$ où $\vec{u}$ est le vecteur unitaire selon l’axe optique.

4. On place un polariseur orthogonalement au faisceau.

Exemple.

Pourquoi le faisceau obtenu forme une quasi-onde plane ?

Méthode 3 : détecter une lumière PR au laboratoire

1. On place un polariseur orthogonalement au faisceau (supposé cylindrique) de lumière. Le polariseur est alors appelé un analyseur.

2. On fait pivoter la lame dans son plan. Si on observe une extinction complète dans une certaine direction, alors la lumière est PR dans la direction orthogonale à l’axe de l’analyseur.

3. Dans ce cas, on peut vérifier la loi de Malus : en notant $\alpha$ l’angle entre la direction de polarisation et celle de l’analyseur, et $I$ l’intensité lumineuse détectée

$\displaystyle{I=I_0\cos^2(\alpha)}$

Exemple.

En projetant $\vec{E}$ sur les axes orthogonaux $\vec{u}$ (direction de polarisation de l’analyseur, axe transparent) et $\vec{v}$ (direction orthogonale dans le plan de la lame, axe opaque), démontrer la loi de Malus.

Le programme de physique-chimie est en accès libre via les cours en ligne de physique-chimie en MP, les cours en ligne de physique-chimie en PSI ou encore les cours en ligne de physique-chimie en PT. Pour la filière PC, les cours sont scindés en 2 parties, à savoir, les cours en ligne de physique en PC et les cours en ligne de chimie en PC.

Rayonnement du dipôle oscillant

Méthode : décrire les caractéristiques de l’onde rayonnée par le dipôle oscillant.

On se place dans l’approximation dipolaire $a\ll\lambda\ll r$

1. L’expression n’est pas à mémoriser. L’onde est décrit en coordonnées sphériques. Le vecteur d’onde est selon $\vec{u}_r$ le champ électrique selon $\vec{u}_{\theta}$ et le champ magnétique selon $\vec{u}_{\varphi}$