Cours en ligne Physique-Chimie en Maths Spé

Chapitres Physique-Chimie en MP, PSI, PC, MPI, TSI, PT

Cours sur l’optique physique en MP, PSI, PC et MPI

Ce cours de physique chimie gratuit destiné aux étudiants en classes préparatoires en maths sup sera très utile pour aborder le sujet de l’optique physique. Nous allons revoir plusieurs notions en physique chimie, notamment Interférences à deux ondes, dispositif d’Young en prépa, Michelson, réseau de diffraction. Si vous souhaitez améliorer votre niveau en physique chimie, nous vous encourageons vivement à envisager nos cours de physique chimie.

Interférences à deux ondes en maths spé

Méthode 1. Superposition d’ondes complexes.

Il n’y a interférences que si

* les deux ondes ont même pulsation

* elles sont issues d’une même source

* leur décalage temporel est très inférieur au temps de cohérence, durée caractéristique des trains d’onde.

Sous ces hypothèses, les deux ondes complexes sont dites cohérentes. Elles interfèrent en $M$ comme des fragments du même train d’onde arrivant par deux chemins différents

$\stackrel{\frown}{(SM)_1}$ et $\stackrel{\frown}{(SM)_2}$

En notant

* $\lambda_0$ la longueur d’onde dans le vide de l’onde

* $\underline{a}_1$ la vibration complexe en $M$ issue de la source $S$ arrivant par le chemin 1

* et $\delta$ la différence de marche entre le chemin 2 et le chemin 1,

on a donc la formule clé :

$\displaystyle{\underline{a}_2=\underline{a}_1\exp\left(-i\frac{2\pi\delta}{\lambda_0}\right)}$

À partir de cette formule, on peut presque tout faire, en particulier établir la formule de Fresnel à deux ondes de même amplitude (cas d’un diviseur d’onde parfait), et celle des réseaux.

S’il existe un facteur d’atténuation $\beta$ (diviseur non parfait) entre les deux ondes alors

$\displaystyle{\underline{a}_2=\beta\underline{a}_1\exp\left(-i\frac{2\pi\delta}{\lambda_0}\right)}$

Démonstration de cours : formule de Fresnel à deux ondes cohérentes de même amplitude.

L’intensité lumineuse due à la seule onde (1) est

$I_1=K\underline{a}_1\underline{a}_1^*$

Celle due à la seule onde (2) est

$I_2=K\underline{a}_1\underline{a}_1^*$

Si on a $I_2=I_1=I_0$ (donc $\beta=1$ ) alors montrer que

$\displaystyle{I=K\underline{a}\underline{a}^*=2I_0\left(1+\cos\frac{2\pi\delta}{\lambda_0}\right)}$

UN APPRENTISSAGE DYNAMIQUE ET COMPLET EN PHYSIQUE

Le confort de l'apprentissage chez vous

Méthode 2. Formules de Fresnel pour les diviseurs d’onde.

Il existe une grande variété de diviseurs d’onde : Michelson, le dispositif d’Young qui sont explicitement au programme, mais aussi d’autres dispositifs à base de miroirs, de prismes ou de lentilles.

La principale difficulté est en général d’ordre géométrique : il faut déterminer la différence de marche $\delta$ entre les deux ondes qui interfèrent en un point $M$ de l’écran, repéré par une coordonnée métrique ou angulaire

( $r$ , $x$ , $y$ , $z$ , $\theta$ , $\varphi$ ).

Notons-la $y$ par exemple.

Ensuite, on applique à peu près toujours la même démarche.

1. On applique la formule de Fresnel

* Si $I_1=I_2=I_0$ alors

$\displaystyle{I=2I_0\left(1+\cos\frac{2\pi\delta}{\lambda_0}\right)}$

* Sinon

$\displaystyle{I=I_1+I_2+2\sqrt{I_1I_2}\cos\frac{2\pi\delta}{\lambda_0}}$

2. On se place maintenant dans le cas où $I_1=I_2$ . On cherche la position des franges brillantes en résolvant

$\displaystyle{I=I_{\mathrm{max}}=4I_0\Leftrightarrow \frac{2\pi\delta}{\lambda_0}=k\cdot 2\pi}$ avec $k$ entier

soit $p=k$ où $\displaystyle{p=\frac{\delta}{\lambda_0}}$ est l’ordre d’interférences.

On en déduit la position $y_k$ de la frange brillante d’ordre $k$ .

3. On en déduit la forme des franges brillantes définie par $y_k=\mathrm{cste}$

4. On en déduit l’éventuel interfrange $i=|y_{k+1}-y_k|$

5. Il est conseillé, mais pas systématiquement demandé, de tracer, à l’échelle, les franges visibles.

Démonstration de cours : contraste maximal des franges.

En posant $I_2=\alpha I_1$ montrer que le contraste des franges est maximal si $I_2=I_1$

Méthode 3. Utilisation de la loi de Malus

La loi de Malus s’énonce ainsi :

Les surfaces d’onde sont orthogonales aux rayons lumineux.

Voici la méthode préconisée pour simplifier le calcul de la différence de marche.

1. On trace, en partant de la source ponctuelle, les surfaces d’onde qui ont la forme d’arcs de cercle, puis, après traversée de lentilles, peuvent devenir des segments (quand les rayons sont parallèles), jusqu’à ce qu’on bute sur un obstacle, par exemple une pupille de diffraction.

2. On nomme les points qui apparaissent sur la figure, en privilégiant l’indice 1 pour les points sur le rayon 1, l’indice 2 pour le rayon 2.

3. On peut aussi rebrousser chemin, en partant du point $M$ sur l’écran et en invoquant le principe de retour inverse de la lumière.

Exemple.

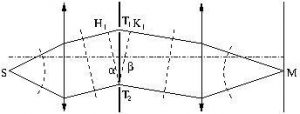
Voici deux rayons issus de $S$ , dans le plan focal objet de la lentille de gauche, qui interfèrent en $M$ , dans le plan focal image de la lentille de droite.

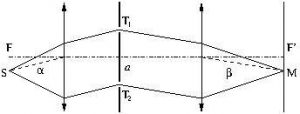
Faire la construction des surfaces d’onde et exprimer $\delta$ en fonction de $\alpha$ , $\beta$ et $a$ , dans l’hypothèse des petits angles.

Dispositif d’Young en prépa

Méthode 1. Calcul de la différence de marche sur un écran loin des fentes.

Un écran est placé à la distance $D$ des fentes d’Young distantes de $a\ll D$ . Une source ponctuelle monochromatique ( $\lambda_0$ ) est placée à égale distance des fentes d’Young.

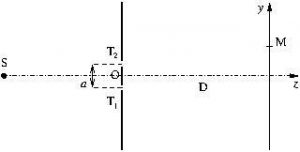
La différence de marche est

$\delta=[ST_1M]-[ST_2M]$

$\delta=[T_2M]-[T_1M]$

On prend l’indice de l’air égal à 1.

La méthode préconisée pour le calcul de la différence de marche est la méthode analytique.

On écrit les coordonnées des trois points

$T_1(0,-a/2)$ , $T_2(0,a/2)$ et $M(D,y)$

On en déduit les composantes des vecteurs

$\vec{T_1M}$ et $\vec{T_2M}$

puis les distances en calculant les normes

$T_1M=\|\vec{T_1M}\|$ et $T_2M=\|\vec{T_2M}\|$

On fait le DL à l’ordre 1 en $a/D\ll 1$ et on en déduit après simplifications

$\delta=\frac{ay}{D}$

Exemple.

Déterminer l’interfrange pour une source monochromatique de longueur d’onde dans le vide $\lambda_0$

Méthode 2. Calcul de la différence de marche dans les conditions de Fraunhoffer

Les conditions d’observation de Fraunhoffer correspondent à une observation à l’infini, dans le plan focal image d’une lentille convergente.

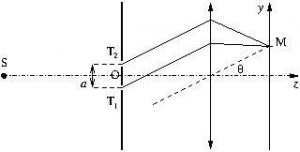
Par application de Malus,

$\delta=a\sin\theta$

Exemple.

Dans l’hypothèse des petits angles, exprimer $\delta$ en fonction de $a$ , $y$ et la distance focale image $f'$ de la lentille convergente.

Méthode 3. Utiliser le critère semi-quantitatif de brouillage des franges par élargissement spatial de la source

Lorsque la source est monochromatique mais large, on l’assimile à une distribution de sources incohérentes deux-à-deux.

Les franges d’interférences sont décalées et se brouillent.

Il y a brouillage si la variation d’ordre d’interférences $\Delta p$ mesurée sur la demi-largeur spatiale de la source est supérieure ou égale à $\frac12$

Voici comment procéder.

1. On construit les deux rayons issus d’un point $C$ au centre de la source et interférant en $M$ . On en déduit l’ordre d’interférences

$\displaystyle{p_C=\frac{\delta_C}{\lambda_0}}$

2. On construit les deux rayons issus d’un point $P$ à la périphérie de la source et interférant en $M$ . On en déduit l’ordre d’interférences

$\displaystyle{p_P=\frac{\delta_P}{\lambda_0}}$

3. On en déduit la variation

$\Delta p=|p_P-p_C|$

4. Il y a brouillage si $\Delta p\geq \frac12$

Justification qualitative.

En raisonnant sur les franges sombres et les franges brillantes données par $C$ et par $P$ , expliquer le brouillage des franges en $M$ si $\Delta p=\frac12$

Méthode 4. Utiliser le critère semi-quantitatif de brouillage des franges par élargissement spectral de la source

Lorsque la source est ponctuelle mais possède un spectre large, on l’assimile à une distribution de sources incohérentes deux-à-deux.

Les franges d’interférences sont décalées et se brouillent.

Il y a brouillage si la variation d’ordre d’interférences $\Delta p$ mesurée sur la demi-largeur spectrale de la source est supérieure ou égale à $\frac12$

Voici comment procéder.

1. On construit les deux rayons issus de la source et interférant en $M$ . On en déduit la différence de marche $\delta$

2. On exprime l’ordre d’interférences au centre de la bande spectrale, pour la longueur d’onde $\lambda_C$

$\displaystyle{p_C=\frac{\delta}{\lambda_C}}$

3. On exprime l’ordre d’interférences à la périphérie de la bande spectrale, pour la longueur d’onde $\lambda_P$

$\displaystyle{p_P=\frac{\delta}{\lambda_P}}$

4. On en déduit la variation

$\Delta p=|p_P-p_C|$

5. Il y a brouillage si $\Delta p\geq \frac12$

Exemple.

Une source ponctuelle possède une bande spectrale

$[\lambda_0-\Delta\lambda/2,\lambda_0+\Delta\lambda/2]$

avec $\Delta\lambda\ll \lambda_0$

Dans le dispositif des trous d’Young distants de $a$ en observation directe sur un écran distant de $D$ , exprimer la condition de brouillage en un point $M$ d’ordonnée $y$ .

COURS DE PHYSIQUE-CHIMIE

Nous avons sélectionné pour vous les meilleurs profs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES

Avis Google France ★★★★★ 4,9 sur 5

Michelson en prépa MP, MPI, PC, PSI et PT

Méthode 1. Faire le repliage partiel du Michelson

Le Michelson comporte une lame semi-réfléchissante et une compensatrice parallèle, et deux miroirs $M_1$ et $M_2$ .

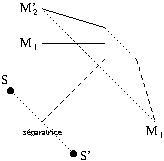
Faire le repliage du Michelson, c’est faire une construction géométrique permettant de se débarrasser du couple séparatrice-compensatrice pour simplifier le calcul de la différence de marche.

1. On construit le symétrique $S'$ de la source $S$ par rapport à la séparatrice.

2. On construit le symétrique $M'_1$ du miroir $M_1$ par rapport à la séparatrice.

On obtient ainsi une source ponctuelle $S'$ et deux miroirs (proches l’un de l’autre, et faisant un angle faible entre eux) $M'_1$ et $M_2$

Méthode 2. Dispositif du coin d’air

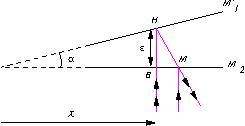
En coin d’air, les centres des deux miroirs $M'_1$ et $M_2$ sont confondus et ils forment entre eux un angle $\alpha$ très petit.

1. Sur le miroir $M_2$ , la différence de marche vaut

$\delta=2\varepsilon$

où $\varepsilon$ est l’épaisseur du coin d’air au point $M$ considéré.

2. Cette différence de marche ne dépend pas de la position de la source. Il n’y a donc pas brouillage même si la source est large, auquel cas on dit que les interférences sont localisées sur $M_2$

3. La frange brillante d’ordre $k$ entier est définie par $p=k$ soit

$2\varepsilon=k\lambda_0$

Les franges forment donc des lignes droites parallèles à l’arête du coin d’air, pour lesquelles $\varepsilon$ est constante, on les appelle donc les franges d’égale épaisseur.

4. En définissant un axe $(O,x)$ sur $M_2$ on a

$\varepsilon=x\tan\alpha\simeq \alpha x$

On en déduit que la frange brillante d’ordre $k$ est une droite d’équation

$\displaystyle{x_k=k\frac{\lambda_0}{2\alpha}}$

5. On en déduit l’interfrange

$\displaystyle{i=|x_{k+1}-x_k|=\frac{\lambda_0}{2\alpha}}$

6. Souvent, on forme l’image de $M_2$ sur un écran grâce à une lentille de projection. On en déduit la position des franges et l’interfrange en appliquant les relations de conjugaison pour la lentille.

Exemple.

La lentille de projection a pour distance focale $f'$ , elle est placée à la distance $D$ de $M_2$ et à la distance $D'$ de l’écran.

Exprimer la relation entre $D$ et $D'$ et l’interfrange $i'$ mesurés sur l’écran.

Méthode 3. Dispositif de la lame d’air

Le Michelson est en lame d’air si les deux miroirs $M'_1$ et $M_2$ sont parallèles et distants de $e$ .

1. On opère le repliage complet du Michelson en traçant les symétriques $S_1$ et $S_2$ de $S'$ par rapport respectivement à $M'_1$ et $M_2$ . On a donc $S_1S_2=2e$

2. On fait une observation à l’infini en plaçant l’écran dans le plan focal image d’une lentille convergente de centre $O$ et de distance focale $f'$ . Un point $M$ de l’écran est repéré par l’angle $i$ entre l’axe de la lentille et $(OM)$ . Les rayons qui interfèrent en $M$ sont parallèles entre eux issus de $S_1$ et de $S_2$

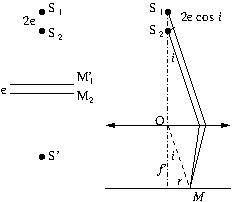
3. La différence de marche se calcule en traçant les surfaces d’onde issues de $M$ , en appliquant la loi de Malus et le principe de retour inverse de la lumière d’où

$\delta=2e\cos i$

4. Cette différence de marche ne dépend pas de la position de la source donc il n’y a pas brouillage quand la source est large, on dit dans ce cas que les interférences sont localisées à l’infini.

5. La frange brillante d’ordre $k$ est définie par $p=k$ avec $k$ entier soit

$2e\cos i=k\lambda_0$

Elle est donc définie par $i=\mathrm{cste}$ , c’est pourquoi on l’appelle frange d’égale inclinaison, elle forme un cercle de centre $F'$ sur l’écran.

6. La non linéarité du cosinus fait que l’interfrange n’est pas régulier, les cercles sont espacés au centre et de plus en plus serrés vers la périphérie.

Attention ! Le numéro de la frange ne correspond pas à l’ordre d’interférences.

Exemple.

Donner l’expression du rayon $r_k$ de la frange brillante d’ordre $k$ sur l’écran, en précisant les valeurs de $k$ possibles.

Méthode 4. Utiliser le Michelson pour mesurer des grandeurs physiques

Voici les principaux axes d’étude.

1. Mesure d’une très petite distance $e$

On mesure les rayons des franges en lame d’air et on en déduit $e$

2. Mesure d’un très petit angle $\alpha$

On mesure l’interfrange des franges en coin d’air et on en déduit $\alpha$

3. Mesure d’indice. On intercale sur l’un des bras du Michelson une cuve d’épaisseur connue.

On part du contact optique : $e=0$ .

On remplit la cuve du fluide dont on cherche l’indice. On compte le nombre de franges qui défilent et on en déduit l’indice du fluide.

4. Analyse d’un défaut.
On se place en coin d’air et on observe la déformation des franges là où se trouve le défaut. On en déduit les caractéristiques du défaut.

5. Mesure d’un doublet spectral (cas typique : doublet jaune du sodium).

On part du contact optique. On chariote et on observe un brouillage périodique des franges. On en déduit l’écart spectral des deux composantes du doublet.

6. Mesure de la largeur d’une raie (cas typique : raie verte du mercure).

On part du contact optique. On chariote et on observe un brouillage définitif des franges. On en déduit la largeur spectrale de la raie.

STAGE INTENSIF EN MATHS SPÉ

Profite de tes vacances pour gagner des points aux concours.

100% obtiennent une école d’ingénieur
58% admissibles Mines-Centrales
99% de recommandation à leurs amis

Avis Google France ★★★★★ 4,9 sur 5

Méthode 5. Michelson en lumière blanche

1. Quand on est rigoureusement au contact optique ( $e=0$ et $\alpha=0$ ), on observe le blanc d’ordre supérieur, c’est-à-dire que toutes les composantes du spectre sont en interférences constructives.

2. On chariote très doucement et $e$ atteint environ un micromètre. On observe alors les teintes de Newton. Pour déterminer la couleur, on cherche quelle est la longueur d’onde éteinte (en interférence destructive, $p$ demi-entier) et on en observe la couleur complémentaire dans le cercle chromatique.

3. On continue de charioter, $e$ atteint quelques micromètres à quelques dizaines de micromètres. On observe cette fois-ci une teinte blanche, mais avec un spectroscope, on distingue le spectre cannelé. On détermine le nombre de cannelures en cherchant le nombre de radiations éteintes dans le spectre de la lumière visible.

Exemple.

Si $e=400~\mathrm{nm}$ quelle est la teinte de Newton observée au centre de l’écran ?

En Maths Spé, il est essentiel d’être à jour sur tous les cours de physique-chimie au programme, sans quoi la réussite aux concours risque d’être compliquée. Pour vous accompagner dans vos révisions, nous vous proposons de nombreux cours en ligne de physique-chimie en PSI, des cours en ligne de MP en physique-chimie et même des cours en ligne de physique-chimie en PT. Nous n’avons pas oublier les étudiants de la filière PC, puisque nous proposons aussi des cours en ligne de physique en PC et des cours en ligne de chimie en PC.

Réseau de diffraction en CPGE

Méthode 1. Formule fondamentale des réseaux : aspect théorique

Attention ! Il est déconseillé de mener le calcul jusqu’au bout pour établir la formule fondamentale des réseaux, la méthode simplifiée (méthode 2) suffit.

Un réseau comporte $n$ traits par mètre, c’est-à-dire une fente tous les $a=1/d$ mètres, et $N$ traits au total.

On éclaire et on observe le réseau à l’infini, donc les rayons incidents sont tous parallèles et font un angle $i$ avec la normale, on observe dans une direction faisant un angle $\theta$ avec la normale.

1. La différence de marche entre deux rayons consécutifs est

$\delta=a(\sin i-\sin\theta)$

2. En appliquant la formule clé, en notant

$\underline{a}_0$

l’onde complexe issue de la fente numéro 0, l’onde issue de la fente numéro $k$ est

$\underline{a}_k=\underline{a}_0\exp(-ik\Phi)$

avec $\displaystyle{\Phi=\frac{2\pi\delta}{\lambda_0}}$

3. On en déduit, en sommant toutes ces ondes cohérentes

$\displaystyle{\underline{a}=\sum_{k=0}^{N-1}\underline{a}_k}$

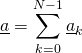
C’est la somme des termes d’une suite géométrique de raison $\exp(-i\Phi)$

On en déduit

$\displaystyle{I=K\underline{a}\underline{a}^*=I_0\frac{\sin^2(N\Phi)}{\sin^2\Phi}}$

On appelle cette expression la fonction de réseau.

4. On démontre (c’est assez pénible à faire) que cette fonction de réseau présente des pics dont la largeur relative diminue rapidement quand $N$ augmente.

Dès que $N$ est supérieur à 10 environ, on n’a plus qu’un « peigne de Dirac », avec des maxima de lumière dans des directions privilégiées définies par

$\Phi=p\cdot 2\pi$ soit

$a(\sin i-\sin \theta)=p\lambda$ , $p$ entier, ce qui forme la formule fondamentale des réseaux.

Méthode 2. Formule fondamentale des réseaux : aspect pratique

1.La différence de marche entre deux rayons consécutifs est

$\delta=a(\sin i-\sin\theta)$

2. S’il y a interférences constructives entre les rayons issus de deux fentes consécutives, par transitivité, il y a interférences constructives entre tous les rayons et donc maximum de lumière. C’est donc le cas si $\delta=p\lambda_0$ , $p$ entier.

3. On admet que cette condition suffisante est aussi nécessaire.

4. On en déduit la formule fondamentale des réseaux

$a(\sin i-\sin \theta)=p\lambda$ , $p$ entier,

Exemple.

Pour $i=0$ , combien de pics sont visibles ?

Complétez vos fiches de cours en révisant et en testant vos connaissances sur d’autres chapitres importants de physique-chimie au programme de maths spé :

Cours sur l’optique physique en MP, PSI, PC et MPI

Interférences à deux ondes en maths spé

Méthode 1. Superposition d’ondes complexes.

UN APPRENTISSAGE DYNAMIQUE ET COMPLET EN PHYSIQUE

Le confort de l'apprentissage chez vous

Méthode 2. Formules de Fresnel pour les diviseurs d’onde.

Méthode 3. Utilisation de la loi de Malus

Dispositif d’Young en prépa

Méthode 1. Calcul de la différence de marche sur un écran loin des fentes.

Méthode 2. Calcul de la différence de marche dans les conditions de Fraunhoffer

Méthode 3. Utiliser le critère semi-quantitatif de brouillage des franges par élargissement spatial de la source

Méthode 4. Utiliser le critère semi-quantitatif de brouillage des franges par élargissement spectral de la source

COURS DE PHYSIQUE-CHIMIE

Nous avons sélectionné pour vous les meilleurs profs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES

Michelson en prépa MP, MPI, PC, PSI et PT

Méthode 1. Faire le repliage partiel du Michelson

Méthode 2. Dispositif du coin d’air

Méthode 3. Dispositif de la lame d’air

Méthode 4. Utiliser le Michelson pour mesurer des grandeurs physiques

STAGE INTENSIF EN MATHS SPÉ

Profite de tes vacances pour gagner des points aux concours.

Méthode 5. Michelson en lumière blanche

Réseau de diffraction en CPGE

Méthode 1. Formule fondamentale des réseaux : aspect théorique

Méthode 2. Formule fondamentale des réseaux : aspect pratique

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales