Cours en ligne Physique-Chimie en Maths Spé
Chapitres Physique-Chimie en MP, PSI, PC, MPI, TSI, PT
Cours sur physique quantique en MP, PSI, PC, MPI
Résumé de cours Exercices et corrigés
Ce cours de physique chimie gratuit spécialement conçu pour les étudiants en maths spé vous sera très utile pour étudier la physique quantique. Au cours du cours en ligne de physique-chimie, nous aborderons les concepts suivants : Solutions stationnaires, grandeurs ![]() ,
, ![]() et
et ![]() , paquet d’ondes, potentiel constant par morceaux et oscillations quantiques. Si vous souhaitez améliorer vos notes, nous vous encourageons vivement à envisager nos cours à domicile en physique chimie.
, paquet d’ondes, potentiel constant par morceaux et oscillations quantiques. Si vous souhaitez améliorer vos notes, nous vous encourageons vivement à envisager nos cours à domicile en physique chimie.
Solutions stationnaires en maths spé
Méthode 1. Séparation des variables
Dans l’équation de Schrödinger (EDS en abrégé) unidimensionnelle pour une particule sans spin et dans un champ d’énergie potentielle indépendante du temps
![]()
![]()
On cherche une solution stationnaire
![]()
On injecte cette expression dans EDS, on divise par ![]() et on obtient
et on obtient
![]()
Cette égalité entre deux termes dont l’un ne dépend que de ![]() et l’autre que de
et l’autre que de ![]() implique leur égalité à une constante indépendante de
implique leur égalité à une constante indépendante de ![]() et de
et de ![]() , homogène à
, homogène à ![]() , on l’identifie à l’énergie
, on l’identifie à l’énergie ![]() de la particule. On en déduit
de la particule. On en déduit
![]()
![]()
Exemple.
Établir l’expression de ![]() . On prendra, en justifiant, la constante d’intégration égale à 1. En déduire la relation de Planck-Einstein.
. On prendra, en justifiant, la constante d’intégration égale à 1. En déduire la relation de Planck-Einstein.
Méthode 2. Résolution de l’EDS spatiale pour un potentiel constant
On pose ![]()
* Si ![]() alors
alors
![]()
*Si ![]() alors
alors
![]()
Exemple.
Donner les expressions de
* la pulsation spatiale ![]() dans le cas
dans le cas ![]()
* l’épaisseur de peau ![]() si
si ![]()
Méthode 3. Interpréter les solutions stationnaires de l’EDS
* La solution
![]()
est une onde progressive dans le sens des ![]() croissants
croissants
* La solution
![]()
est une onde progressive dans le sens des ![]() décroissants
décroissants
* La solution
![]()
est une onde stationnaire (parfois qualifiée d’évanescente selon le sens pour ![]() et le signe devant
et le signe devant ![]() ).
).
Exemple.
Pourquoi dit-on que
![]()
est progressive dans le sens des ![]() croissants ?
croissants ?
Grandeurs  ,
,  et
et 
Méthode 1. Densité de probabilité de présence
![]() est une grandeur complexe ondulatoire. Le carré de sa norme est la densité linéique de probabilité de présence
est une grandeur complexe ondulatoire. Le carré de sa norme est la densité linéique de probabilité de présence
![]()
où l’étoile désigne le conjugué. Par définition
![]()
où ![]() est la probabilité que la particule se trouve dans l’intervalle
est la probabilité que la particule se trouve dans l’intervalle ![]() à la date
à la date ![]() .
.
Exemple.
Montrer que pour une solution stationnaire
![]() de EDS, la densité linéique de probabilité de présence ne dépend pas de
de EDS, la densité linéique de probabilité de présence ne dépend pas de ![]()
Méthode 2. Normalisation et calcul d’une probabilité de présence sur un intervalle
La probabilité est normalisée
![]()
La probabilité de présence de la particule dans l’intervalle ![]() est
est
![]()
Exemple.
Calculer la norme du complexe ![]() pour la solution stationnaire
pour la solution stationnaire
![]() pour
pour ![]()
et ![]() partout ailleurs.
partout ailleurs.
Méthode 3. Vecteur densité de courant de probabilité de présence
Pour une onde progressive
![]()
le vecteur densité de courant de probabilité de présence est
![]()
![]()
Exemple.
Quelle est l’unité de ![]() ? En déduire son sens physique.
? En déduire son sens physique.
Paquet d’ondes en MP, PC, PSI, MPI
Méthode 1. Étude d’un paquet d’ondes pour une particule libre
Une particule libre est soumise à ![]() pour tout
pour tout ![]() et d’énergie
et d’énergie ![]() .
.
La solution stationnaire
![]()
avec ![]() et
et ![]() n’est pas normalisable. La particule est assimilée à un paquet d’ondes d’extension spatiale
n’est pas normalisable. La particule est assimilée à un paquet d’ondes d’extension spatiale ![]() et de largeur spectrale
et de largeur spectrale ![]() .
.
Un résultat de la théorie spectrale de Fourier donne ![]()
La vitesse de la particule s’identifie à la vitesse de l’enveloppe du paquet d’ondes, donc à la vitesse de groupe
![]()
Démonstrations de cours
Démontrer les trois résultats fondamentaux suivants.
1. Relation de de Broglie : en notant ![]() la quantité de mouvement de la particule
la quantité de mouvement de la particule
![]() donc
donc ![]()
2. Inégalité de Heisenberg spatiale
![]()
3. Énergie cinétique
![]()
Méthode 2. Densité de courant de probabilité de présence pour une particule libre.
En utilisant la relation de de Broglie
![]()
Exemple.
Vérifier sur cette expression l’unité et le sens physique de ![]() (voir partie 2, méthode 3).
(voir partie 2, méthode 3).
UN APPRENTISSAGE DYNAMIQUE ET COMPLET EN PHYSIQUE
Le confort de l'apprentissage chez vous
Potentiel constant par morceaux
Méthode 1. Solution stationnaire par morceaux
Le potentiel est constant par morceaux, il forme une fonction en escaliers sur la droite réelle. Soit ![]() l’énergie et
l’énergie et ![]() la masse d’une particule.
la masse d’une particule.
Pour chaque intervalle, on distingue deux cas.
* Si ![]() , on pose
, on pose ![]() et
et
![]()
![]()
soit ![]()
![]()
qu’on interprète par la superposition de deux ondes harmoniques se propageant dans le sens croissant et dans le sens décroissant des ![]() .
.
* SI ![]() , on pose
, on pose 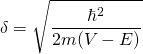 et
et
![]()
![]()
En particulier, si ![]() ,
, ![]()
On a donc deux constantes pour chaque intervalle. On écrit les relations de continuité en chaque point de discontinuité du potentiel.
* ![]() est toujours continue
est toujours continue
* Si la hauteur de la discontinuité du potentiel est finie, ![]() est continue.
est continue.
Exemple.
Le puits de potentiel infini est formé par
![]() si
si ![]() et
et ![]() ailleurs.
ailleurs.
Déterminer la solution générale (en supposant ![]() ) et les deux relations de continuité (sans résoudre le système).
) et les deux relations de continuité (sans résoudre le système).
Méthode 2. Exploiter les relations pour prouver la quantification de l’énergie
Il est parfois possible d’éliminer les constantes entre les relations de continuité, et d’en déduire une relation entre les pulsations spatiales (![]() ) et les épaisseurs de peau (
) et les épaisseurs de peau (![]() ) dans les différents intervalles. Comme ces grandeurs ne dépendent que de
) dans les différents intervalles. Comme ces grandeurs ne dépendent que de ![]() et des différents paramètres (les valeurs des potentiels et
et des différents paramètres (les valeurs des potentiels et ![]() ), on en déduit une équation dont l’unique inconnue est
), on en déduit une équation dont l’unique inconnue est ![]() .
.
La présence d’exponentielles complexes dans cette équation conduit à des équations trigonométriques, qui admettent des solutions discrètes, d’où quantification de ![]() . Il est fréquent qu’on recoure à une résolution graphique.
. Il est fréquent qu’on recoure à une résolution graphique.
Exemple.
Expliciter les valeurs quantifiées de ![]() ,
, ![]() et
et ![]() pour la particule dans le puits de potentiel infini.
pour la particule dans le puits de potentiel infini.
Méthode 3. Exploiter les relations pour calculer un coefficient de réflexion
Le cas d’école est la marche de potentiel.
En un point de discontinuité, on détermine le rapport entre le coefficient complexe de l’onde complexe « réfléchie » qui se propage dans le sens des ![]() décroissants et celui de l’onde complexe « incidente » qui se propage dans le sens des
décroissants et celui de l’onde complexe « incidente » qui se propage dans le sens des ![]() croissants.
croissants.
On en déduit le coefficient de réflexion en densités de courant entre l’onde réfléchie et l’onde incidente.
Exemple
Une particule d’énergie ![]() et de masse
et de masse ![]() aborde une marche de potentiel
aborde une marche de potentiel
(![]() pour
pour ![]() négatif)
négatif)
![]() (
(![]() pour
pour ![]() positif).
positif).
Déterminer le coefficient de réflexion et de transmission de l’onde en fonction de
![]()
et ![]()
On supposera que les particules arrivent de ![]()
Restez motivés et entrainez-vous grâce aux autres cours en ligne de Maths Spé à votre disposition, comme les cours en ligne de physique-chimie en MP, ou bien les cours en ligne de physique-chimie en PSI et bien sûr, les cours en ligne de physique-chimie en PT. Pour vous, les étudiants de PC, révisez sur les cours en ligne de chimie de PC ainsi que sur les cours en ligne de physique en PC.
STAGE INTENSIF EN PRÉPA SCIENTIFIQUE
Profite de tes vacances pour progresser en vue des concours.
96% de réussite aux concours
44% dans le TOP 10
99% de recommandation
Avis Google France ★★★★★ 4,9 sur 5
Oscillations quantiques
Méthode. Expliciter la superposition de deux solutions stationnaires et observer qu’elle n’est pas stationnaire
On forme la superposition de deux solutions stationnaires d’énergies différentes ![]() et
et ![]()
![]()
On exprime la densité de probabilité
![]()
On met en évidence les termes carrés
![]() et
et ![]()
qui sont indépendants du temps
et la somme des termes rectangles qui s’exprime par une fonction cosinusoÏdale du temps, de pulsation
![]()
Démonstration de cours que les oscillations quantiques
Démontrer la propriété énoncée.
L’année de maths spé est très courte et les concours arrivent très vite, d’intenses et régulières révisions sont donc indispensables. Revoyez par exemple, les chapitres suivants au programme de physique-chimie en maths spé :

