Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Polynômes en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Résumé de cours et méthodes – Polynômes
Méthode 1 : Egalité de deux polynômes.
Deux polynômes ![]() et
et ![]() sont égaux si, et seulement si,
sont égaux si, et seulement si, ![]() et s’ils ont les mêmes coefficients.
et s’ils ont les mêmes coefficients.
Exemple : Montrer l’égalité suivante, dite égalité de Vandermonde :
![Rendered by QuickLaTeX.com \[\text{Pour tout} \; n \in \mathbb N^*, \qquad\binom{2n}{n} = \sum_{k=0}^n \binom{n}{k}^2\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ea0c8a07df401aee603b897b4ba1f843_l3.png)
Indication : En partant de l’égalité ![]() on identifiera les coefficients de
on identifiera les coefficients de ![]()
Réponse :
![]() Développons
Développons ![]() à l’aide de la formule du binôme de Newton : on a
à l’aide de la formule du binôme de Newton : on a
![Rendered by QuickLaTeX.com \[\left( 1 + X \right)^{2n} = \sum_{k=0}^{2n} \binom{2n}{k} X^k.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-95282fdddefce3f113dfe11cf7750ce8_l3.png)
Le coefficient de
![]() Simplifions
Simplifions ![]() à l’aide du binôme de Newton : on a
à l’aide du binôme de Newton : on a
![]()
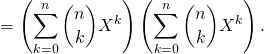
On rappelle que si 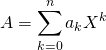 et
et 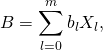 alors
alors 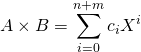 avec
avec ![]() Le coefficient de
Le coefficient de ![]() est
est 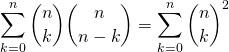 (n’hésitez pas à développer le produit si vous ne voyez pas pourquoi !)
(n’hésitez pas à développer le produit si vous ne voyez pas pourquoi !)
D’où :
![Rendered by QuickLaTeX.com \[\binom{2n}{n} = \displaystyle\sum_{k=0}^n \binom{n}{k}^2.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6f7461bc93c4e22ec4d5af031c1be1e9_l3.png)
Si vous êtes confronté à des lacunes en maths, nos profs de maths en ligne s’adressent spécialement aux étudiants de terminale pour les aider à surmonter les blocages en ECG1.
Méthode 2 : Sur l’ordre des racines d’un polynôme.
Nous rappelons que ![]() est racine d’ordre
est racine d’ordre ![]() (
(![]() ) de
) de ![]()
![]() et
et ![]()
![]() il existe un polynôme
il existe un polynôme ![]() tel que
tel que ![]() avec
avec ![]()
Conséquence : si ![]() et
et ![]()
![]() divise
divise ![]() si, et seulement si,
si, et seulement si, ![]() est racine d’ordre au moins
est racine d’ordre au moins ![]() de
de ![]() si, et seulement si,
si, et seulement si,
![]()
Exemple : Donner une condition nécessaire et suffisante sur ![]() pour que
pour que ![]() soit divisible par
soit divisible par ![]()
Réponse :
La condition : ![]() est divisible par
est divisible par ![]() signifie que
signifie que ![]() est racine d’ordre au moins
est racine d’ordre au moins ![]() pour
pour ![]() Ainsi, cela est équivalent à :
Ainsi, cela est équivalent à : ![]() Ces conditions donnent le système d’équations suivant :
Ces conditions donnent le système d’équations suivant :
![Rendered by QuickLaTeX.com \[\begin{cases} a + b + 1 & = 0 \\ \left( n + 1 \right) a + n b & =0 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e27614ed7f0b038dc2f50a331f08883b_l3.png)
Cela donne
Méthode 3 : Sur la division euclidienne.
La division euclidienne est une pratique fondamentale à maîtriser.
Nous rappelons aussi le résultat général : soient ![]() et
et ![]() deux polynômes de
deux polynômes de ![]() avec
avec ![]()
Alors il existe deux polynômes de ![]() disons
disons ![]() et
et ![]() uniques tels que :
uniques tels que :
![]()
avec
Exemple : Que vaut le reste ![]() de la division euclidienne de
de la division euclidienne de ![]() par
par ![]() ?
?
(i) ![]()
(ii) ![]()
(iii) ![]()
Réponse :
On remarque que ![]()
![]() ainsi
ainsi ![]() et
et ![]()
Méthode 4 : Une méthode pratique pour déterminer le reste de la division euclidienne.
Soient ![]() et
et ![]() deux polynômes de
deux polynômes de ![]() avec
avec ![]() On suppose que
On suppose que ![]() avec
avec ![]() des scalaires deux à deux distincts. On écrit alors
des scalaires deux à deux distincts. On écrit alors ![]() avec
avec ![]() ainsi
ainsi ![]() Puis en évaluant en
Puis en évaluant en ![]() pour
pour ![]() on a
on a
![]()
Cela donne un système de
Exemple : Que vaut le reste ![]() de la division euclidienne de
de la division euclidienne de ![]() par
par ![]() ?
?
(i) ![]()
(ii) ![]()
(iii) ![]()
Réponse : Comme ![]() le degré du reste est au plus
le degré du reste est au plus ![]() ainsi on pose
ainsi on pose ![]() Donc
Donc ![]() En évaluant cette relation en
En évaluant cette relation en ![]() et
et ![]() on a le système suivant :
on a le système suivant :
Méthode 5 : Factoriser un polynôme.
En conséquence du théorème de d’Alembert-Gauss, on rappelle qu’un polynôme se factorise dans ![]() comme produit de polynômes de degré
comme produit de polynômes de degré ![]() .
.
Dans ![]() pour factoriser un polynôme de degré
pour factoriser un polynôme de degré ![]() il faut chercher ses
il faut chercher ses ![]() racines (éventuellement confondues).
racines (éventuellement confondues).
Dans ![]() la situation est différente. On rappelle qu’un polynôme réel se factorise comme produit de polynômes de degré
la situation est différente. On rappelle qu’un polynôme réel se factorise comme produit de polynômes de degré ![]() et de polynômes de degré
et de polynômes de degré ![]() ayant un discriminant strictement négatif. Ainsi, pour factoriser un polynôme dans
ayant un discriminant strictement négatif. Ainsi, pour factoriser un polynôme dans ![]() on cherche ses racines réelles et complexes non réelles que l’on regroupe deux à deux.
on cherche ses racines réelles et complexes non réelles que l’on regroupe deux à deux.
Si ![]() est racine, alors
est racine, alors ![]() est aussi racine de
est aussi racine de ![]() et
et
![]() divise
divise ![]() .
.
Exemple : Factoriser dans ![]() le polynôme
le polynôme ![]()
Réponse :
Cherchons les racines de ![]() : il faut donc résoudre l’équation
: il faut donc résoudre l’équation ![]() On remarque que
On remarque que ![]() est solution particulière. Par la méthode 5 du chapitre Nombres Complexes, on récupère toutes les autres racines en multipliant
est solution particulière. Par la méthode 5 du chapitre Nombres Complexes, on récupère toutes les autres racines en multipliant ![]() par les racines
par les racines ![]() -ièmes de l’unit\’e. Comme le coefficient dominant est
-ièmes de l’unit\’e. Comme le coefficient dominant est ![]() on peut écrire
on peut écrire![]()
![]()
![]()
Pour factoriser ce polynôme dans ![]() il faut remarquer que
il faut remarquer que ![]() et
et ![]() En écrivant
En écrivant ![]()
![]()
![]()
et en développant, on obtient
![]()
![]()
![]()
![]() .
.
Méthode 6 : Calculer les racines carrées d’un nombre complexe en l’absence d’une forme exponentielle simple.
Pour factoriser un polynôme, on vient de voir qu’il faut trouver ses racines. Citons quelques approches (non exhaustives) pour démarrer !
![]() Pour un polynôme de degré au moins
Pour un polynôme de degré au moins ![]() il y a peut-être une racine « évidente » (par racine évidente, on entend
il y a peut-être une racine « évidente » (par racine évidente, on entend ![]() ou
ou ![]() ).
).
![]() Si l’on sait que
Si l’on sait que ![]() est racine d’un polynôme reel, alors
est racine d’un polynôme reel, alors ![]() est aussi racine (cette remarque n’a d’intérêt que si
est aussi racine (cette remarque n’a d’intérêt que si ![]() ).
).
![]() Pour les polynômes du type
Pour les polynômes du type ![]() en posant
en posant ![]() on se ramène \`a un polynôme de degré
on se ramène \`a un polynôme de degré ![]()
![]() Il est toujours bon de se rappeler que le polynôme
Il est toujours bon de se rappeler que le polynôme ![]() a pour racines les racines
a pour racines les racines ![]() -ièmes de l’unité.
-ièmes de l’unité.
Exemple : Quelles sont les racines du polynôme ![]() ?
?
(i) 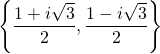
(ii) 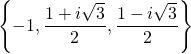
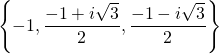
Réponse :
On remarque que ![]() est racine évidente de
est racine évidente de ![]() Ainsi
Ainsi ![]() se factorise par
se factorise par ![]() de la façon suivante :
de la façon suivante : ![]()
Par un simple calcul, on obtient les racines de ![]()
![]() et
et ![]()
Les racines de ![]() sont :
sont : ![]() et
et ![]()
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Méthode 7 : Montrer qu’un polynôme est nul.
Soit ![]() un polynôme de degré
un polynôme de degré ![]() On suppose que
On suppose que ![]() a au moins
a au moins ![]() racines distinctes, alors
racines distinctes, alors ![]() En particulier, si
En particulier, si ![]() a une infinité de racines, alors
a une infinité de racines, alors ![]()
Réponse : On pose ![]() On remarque que
On remarque que ![]()
Il est facile de montrer, par récurrence que ![]() pour tout entier naturel
pour tout entier naturel ![]() Le polynôme
Le polynôme ![]() admet donc une infinité de racines, c’est donc le polynôme nul, ce qui prouve que
admet donc une infinité de racines, c’est donc le polynôme nul, ce qui prouve que ![]() est donc constant.
est donc constant.
Réciproquement, il est clair que les polynômes constants vérifient la relation
![]()
L’ensemble des polynômes vérifiant la relation
Si vous êtes parfaitement au point sur ce chapitre, prenez de l’avance sur le programme de Maths en ECG1 avec les chapitres de maths suivants :

