Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Probabilités sur un univers fini en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Résumé de cours et méthodes – Probabilités sur un univers fini
1. Dénombrement et combinatoire
Méthode 1 : Tirages successifs avec remise.
Si l’on tire ![]() boules successivement et avec remise dans une urne contenant
boules successivement et avec remise dans une urne contenant ![]() boules, il y a
boules, il y a ![]() tirages possibles. On peut facilement s’en convaincre en raisonnant de la manière suivante : il y a
tirages possibles. On peut facilement s’en convaincre en raisonnant de la manière suivante : il y a ![]() choix possibles pour la première boule, il y a
choix possibles pour la première boule, il y a ![]() choix pour la deuxième, etc.
choix pour la deuxième, etc.
Ces tirages s’appellent des ![]() -listes sans répétition des
-listes sans répétition des ![]() boules. Il est conseillé de prendre des cours de soutien de maths pour progresser sur les probabilités sur un univers fini en ECG1
boules. Il est conseillé de prendre des cours de soutien de maths pour progresser sur les probabilités sur un univers fini en ECG1
Exemple : 1) Soient ![]() et
et ![]() avec
avec ![]() . Dénombrer le nombre d’applications de
. Dénombrer le nombre d’applications de ![]() vers
vers ![]()
2) On lance trois fois de suite un dé.
a) Combien y a-t-il de lancers possibles ?
b) Combien y a-t-il de lancers où le premier dé donne un multiple de ![]() ?
?
c) Combien y a-t-il de lancers où l’on obtient les chiffres ![]() et
et ![]() ?
?
Réponse :
1) Définir une application de ![]() vers
vers ![]() c’est associer à chaque élément de
c’est associer à chaque élément de ![]() un unique élément de
un unique élément de ![]() Autrement dit, cela revient à choisir successivement et avec remise
Autrement dit, cela revient à choisir successivement et avec remise ![]() fois (car
fois (car ![]() ) un élément de
) un élément de ![]() qui contient
qui contient ![]() éléments. Ainsi, il y a
éléments. Ainsi, il y a ![]() choix possibles donc il y a
choix possibles donc il y a ![]() applications de
applications de ![]() vers
vers ![]()
2) a) Chaque lancer donne ![]() résultats possibles, comme les trois lancers sont successifs, on en a au final
résultats possibles, comme les trois lancers sont successifs, on en a au final ![]() lancers possibles.
lancers possibles.
Méthode 2 : Tirages successifs sans remise.
Soient ![]() tels que
tels que ![]() Si l’on tire
Si l’on tire ![]() boules de manière successive et sans remise dans une urne contenant
boules de manière successive et sans remise dans une urne contenant ![]() boules, il y a
boules, il y a ![]() tirages possibles. On appelle
tirages possibles. On appelle ![]() -listes sans répétition des
-listes sans répétition des ![]() boules tout résultat d’un tel tirage et on note
boules tout résultat d’un tel tirage et on note ![]() le nombre de ces tirages.
le nombre de ces tirages.
On peut s’en convaincre en raisonnant de la façon suivante : il y a ![]() choix pour la première boule,
choix pour la première boule, ![]() pour la deuxième, etc. Pour la
pour la deuxième, etc. Pour la ![]() -ième, il y a
-ième, il y a ![]() choix.
choix.
En particulier, il y a ![]() façons de vider une urne contenant
façons de vider une urne contenant ![]() boules en tirant les boules l’une après l’autre.
boules en tirant les boules l’une après l’autre.
On retiendra que l’ordre importe.
Exemple : Les deux questions sont indépendantes.
1) Soient ![]() et
et ![]() avec
avec ![]() tels que
tels que ![]() Dénombrer le nombre d’applications injectives de
Dénombrer le nombre d’applications injectives de ![]() vers
vers ![]()
2) Au départ d’une course de ![]() mètres, il y a
mètres, il y a ![]() coureurs. Combien y a-t-il de podiums possibles ? On suppose qu’il n’y aura pas d’ex-æquo.
coureurs. Combien y a-t-il de podiums possibles ? On suppose qu’il n’y aura pas d’ex-æquo.
Réponse : 1) Définir une application de ![]() vers
vers ![]() injective, c’est prendre successivement et sans remise (pour bien définir une application injective)
injective, c’est prendre successivement et sans remise (pour bien définir une application injective) ![]() éléments de
éléments de ![]() Il y a donc
Il y a donc ![]() applications injectives de
applications injectives de ![]() vers
vers ![]() .
.
2) Définir un podium, c’est donner un premier, un deuxième et un troisième. Autrement dit, c’est effectuer « trois tirages successifs et sans remise des ![]() coureurs au départ ». Il y a donc
coureurs au départ ». Il y a donc ![]() podiums possibles.
podiums possibles.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
Méthode 3 : Tirages simultanés.
Soient ![]() tels que
tels que ![]() Le nombre de tirages simultanés de
Le nombre de tirages simultanés de ![]() boules dans une urne contenant
boules dans une urne contenant ![]() boules est égal à
boules est égal à ![]() tirages.
tirages.
On retiendra que l’ordre n’importe pas.
Exemple : a) De combien de façons peut-on donner une main de ![]() cartes d’un jeu de
cartes d’un jeu de ![]() cartes ?
cartes ?
b) Combien de ces mains contiendront exactement un roi ?
c) Combien de ces mains contiendront exactement un roi et deux reines ?
Réponse :
a) Donner une main de ![]() cartes à un joueur, cela revient à choisir simultanément
cartes à un joueur, cela revient à choisir simultanément ![]() cartes dans le jeu de
cartes dans le jeu de ![]() cartes : il y a
cartes : il y a ![]() mains possibles.
mains possibles.
b) Se donner une main contenant exactement un roi, c’est choisir un roi parmi les ![]() rois puis choisir simultanément
rois puis choisir simultanément ![]() cartes parmi les
cartes parmi les ![]() cartes restantes. Il y a donc
cartes restantes. Il y a donc ![]()
c) Choisir une main contenant exactement un roi et deux reines, c’est d’abord choisir un roi parmi les ![]() rois puis choisir deux reines parmi les
rois puis choisir deux reines parmi les ![]() et enfin choisir
et enfin choisir ![]() cartes parmi les
cartes parmi les ![]() cartes restantes (celles qui ne sont ni des rois ni des reines). Il y a donc
cartes restantes (celles qui ne sont ni des rois ni des reines). Il y a donc ![]() mains.
mains.
Méthode 4 : Introduire une bijection.
Il suffit de trouver une bijection entre ![]() l’ensemble à dénombrer, et un autre ensemble dont on connaît le nombre d’éléments.
l’ensemble à dénombrer, et un autre ensemble dont on connaît le nombre d’éléments.
Exemple : Soit ![]() et
et ![]() un entier tel que
un entier tel que ![]() Déterminer le nombre de
Déterminer le nombre de ![]() -listes strictement croissantes de
-listes strictement croissantes de ![]()
Réponse : On note ![]() et
et ![]() l’ensemble des parties de
l’ensemble des parties de ![]() contenant
contenant ![]() éléments.
éléments.
L’application ![Rendered by QuickLaTeX.com \begin{cases} \mathcal S_{n ,p} \to \mathcal P_p \left( [\![ 1, n ]\!] \right) \\ \left( i_1 , \cdots , i_p \right) \mapsto \left\{ i_1 , \cdots , i_p \right\} \end{cases}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b330e610452aca0e42fe5a11381f02ac_l3.png) est une bijection (toute partie à
est une bijection (toute partie à ![]() éléments peut être rangée d’une unique façon en une suite strictement croissante), donc
éléments peut être rangée d’une unique façon en une suite strictement croissante), donc
2. Probabilités sur un ensemble fini
Méthode 5 : Vérifier que l’on a défini une probabilité sur ![]() .
.
Soit ![]() un ensemble non vide, on rappelle que
un ensemble non vide, on rappelle que ![]() désigne l’ensemble des parties de
désigne l’ensemble des parties de ![]()
Pour montrer qu’une application ![]() définie sur
définie sur ![]() est une probabilité sur
est une probabilité sur ![]() , il faut montrer qu’elle vérifie les deux points :
, il faut montrer qu’elle vérifie les deux points :
![]()
![]()
![]() si
si ![]() et si
et si ![]() alors
alors ![]()
On notera, lorsque ![]() est fini que,
est fini que, ![]() est entièrement définie sur les ensembles de la forme
est entièrement définie sur les ensembles de la forme ![]() avec
avec ![]()
De plus, pour toute partie ![]() on a
on a
![]()
En particulier si ![]() on a
on a
![]()
Lorsque ![]() pour tout
pour tout ![]() on dit que l’on est sous l’hypothèse d’équiprobabilité. Dans ce cas, pour tout
on dit que l’on est sous l’hypothèse d’équiprobabilité. Dans ce cas, pour tout ![]() on a
on a
![]()
Exemple : Soit ![]() Soit
Soit ![]()
1) Déterminer ![]() tel que l’application
tel que l’application ![]() définie par : pour tout
définie par : pour tout ![]()
![]() définisse une probabilité sur
définisse une probabilité sur ![]()
2) Calculer ![]() où
où ![]() est constitué des nombres pairs de
est constitué des nombres pairs de ![]()
Réponse :
1) ![]() définit une probabilité si sur
définit une probabilité si sur ![]() , et seulement si,
, et seulement si, ![]() prend des valeurs positives et si
prend des valeurs positives et si
![]()
![Rendered by QuickLaTeX.com \[\displaystyle\sum_{k=0}^{2n} a 2^k = 1.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-185e30dc9a67ec18f641ade5ab5993e8_l3.png)
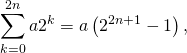 ainsi
ainsi 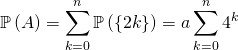
Méthode 6 : Savoir utiliser les relations fondamentales de probabilité.
Rappelons les relations qui servent tout le temps en probabilité, ![]() étant une probabilité sur
étant une probabilité sur ![]()
![]() et
et ![]() étant deux événements :
étant deux événements :
![]()
![]()
![]()
![]()
![]() la formule du crible pour
la formule du crible pour ![]() événements
événements ![]() et
et ![]() :
:
![]()
![]()
![]()
![]() ,
,
![]() si
si ![]() sont
sont ![]() événements deux à deux incompatibles, alors
événements deux à deux incompatibles, alors
![Rendered by QuickLaTeX.com \[\mathbb{P} \left( \displaystyle\bigcup_{k=1}^m A_k \right) = \displaystyle\sum_{k=1}^m \mathbb{P} \left( A_k \right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-83494d238daf1acb805d4a72e0c7abc2_l3.png)
Exemple : Dans une urne, on place ![]() jetons de couleur rouge numérotés de
jetons de couleur rouge numérotés de ![]() à
à ![]()
![]() jetons de couleur blanche numérotés de
jetons de couleur blanche numérotés de ![]() à
à ![]() et
et ![]() jetons de couleur noire numérotés de
jetons de couleur noire numérotés de ![]() à
à ![]() On tire simultanément
On tire simultanément ![]() jetons. On introduit les événements :
jetons. On introduit les événements : ![]() « on a obtenu deux numéros
« on a obtenu deux numéros ![]() « ,
« , ![]() « on a obtenu un seul numéro
« on a obtenu un seul numéro ![]() » et
» et ![]() « on a obtenu deux numéros distincts ».
« on a obtenu deux numéros distincts ».
Calculer ![]() et
et ![]()
Réponse :
On se place dans le cadre de l’équiprobabilité. ![]() est l’ensemble des tirages simultanés de
est l’ensemble des tirages simultanés de ![]() jetons parmi les
jetons parmi les ![]() jetons donc
jetons donc ![]()
L’événement
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 7 : Utiliser la formule des probabilités conditionnelles et la formule des probabilités composées.
1) Par définition, si ![]() n’est pas un événement impossible (i.e.
n’est pas un événement impossible (i.e. ![]() )
) ![]() Cette formule sert aussi sous la forme :
Cette formule sert aussi sous la forme :
![]()
On retiendra que l’application
![Rendered by QuickLaTeX.com \begin{cases} \mathcal P \left( \Omega \right) \to \left[ 0 , 1 \right] \\ B \mapsto \mathbb{P}_A \left( B \right) \end{cases}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6638443ea18a22983420b826caf79ac4_l3.png) définit une probabilité sur
définit une probabilité sur 2) Formule des probabilités composées.
Soient ![]() des événements tels que
des événements tels que ![]() Alors,
Alors,
![]()
Il faut penser à utiliser cette formule en particulier dans les cas suivants :
![]() dans les situations où il y a des urnes dont la composition change à chaque tour,
dans les situations où il y a des urnes dont la composition change à chaque tour,
![]() de manière générale, dans toutes les situations où ce qui se passe à l’instant
de manière générale, dans toutes les situations où ce qui se passe à l’instant ![]() dépend de ce qui se passe aux instants
dépend de ce qui se passe aux instants ![]() 1) Par définition, si
1) Par définition, si ![]() n’est pas un événement impossible (i.e.
n’est pas un événement impossible (i.e. ![]() )
) ![]() Cette formule sert aussi sous la forme :
Cette formule sert aussi sous la forme :
![]()
On retiendra que l’application
![Rendered by QuickLaTeX.com \begin{cases} \mathcal P \left( \Omega \right) \to \left[ 0 , 1 \right] \\ B \mapsto \mathbb{P}_A \left( B \right) \end{cases}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6638443ea18a22983420b826caf79ac4_l3.png) définit une probabilité sur
définit une probabilité sur Quelle est la probabilité de tirer ![]() boules blanches ?
boules blanches ?
Réponse :
On note ![]() l’événement « la
l’événement « la ![]() -ème boule tirée est blanche ».
-ème boule tirée est blanche ».
La probabilité recherchée est :
Clairement

