Chapitres Maths en ECG1

Cours : Raisonnement et vocabulaire ensembliste

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices Corrigés

Cours en ligne de Maths en ECG1

Résumé de cours et méthodes – Raisonnement et vocabulaire ensembliste

1. Quantificateurs, ensemble, logique et raisonnement

Méthode 1 : Utilisation des quantificateurs:

Il y a deux quantificateurs principaux : $\forall$ qui signifie « pour tout » et $\exists$ qui signifie « il existe ». A première vue, cela paraît simple mais il est indispensable de bien les maîtriser ! Compléter votre maîtrise avec des cours particuliers de maths en ligne pour les ECG1.

Il faut faire attention à l’ordre des quantificateurs et toujours les placer avant la proposition à laquelle ils se rapportent.

Exemple : Dire si la phrase mathématique suivante est vraie ou fausse et justifier :

$\exists x \in \mathbb{R}, \; \forall y \in \mathbb{R} , \; y \le x.$

Réponse :

Cette phrase est fausse ! L’ordre des quantificateurs est très important. Il faut reformuler la question de la manière suivante : « peut-on trouver $x \in \mathbb {R}$ , tel que tout pour $y \in \mathbb {R}$ , on ait $y \le x$ ? ».

Un tel $x$ ne peut pas être trouvé ! En effet, si un tel $x$ existait, il suffirait de prendre $y = x + 1$ pour avoir $y > x.$

Méthode 2 : Donner la négation d’une assertion :

Le point de base est de connaître la négation des quantificateurs.
On rappelle que la négation d’un « il existe » est « quel que soit » et que la négation d’un « quel que soit » est « il existe ».

Exemple : Soit l’assertion suivante :
$\exists M \in \mathbb{R} , \, \forall n \in \mathbb{N}, \, u_n \le M.$

Quelle est sa négation ?

Réponse : On applique les règles énoncées ci-dessus. On a :

$\forall M \in \mathbb{R}, \, \exists n \in \mathbb{N}, \, u_n > M,$

Méthode 3 : Implication, condition nécessaire, condition suffisante, CNS :

Soient $P$ et $Q$ deux assertions.

On appelle l’implication $P \Rightarrow Q$ l’assertion $\text{non} \left( P \right) \, \text{ou } \, Q.$ Le seul cas où l’implication $P \Rightarrow Q$ est fausse est le cas où $P$ est vraie et $Q$ est fausse.

Dans le cas où $P \Rightarrow Q$ est vraie, on dit que $P$ est une condition suffisante à $Q$ ou bien que $Q$ est une condition nécessaire à $P.$

On notera que la négation de $P \Rightarrow Q$ est l’assertion $P \, \text{et} \, \text{non} \left( Q \right).$

On dit que l’assertion $P \Leftrightarrow Q$ est vraie lorsque $P \Rightarrow Q$ et $Q \Rightarrow P$ le sont, c’est-à-dire lorsque $P$ et $Q$ sont vraies (respectivement fausses) simultanément.

En pratique :

$\bullet$ Pour montrer $P \Rightarrow Q,$ on montre que si $P$ est vraie, alors $Q$ est vraie aussi.
$\bullet$ Pour montrer $P \Rightarrow Q,$ il est équivalent de montrer que $\text{non} \left( Q \right) \Rightarrow \text{non} \left( P \right)$ (raisonnement par contraposée).
$\bullet$ Pour montrer $P \Leftrightarrow Q,$ on montre $P \Rightarrow Q$ et $Q \Rightarrow P.$ On fera bien attention à bien séparer les deux étapes.
$\bullet$ Pour montrer l’équivalence entre $3$ assertions $P, Q$ et $R,$ il suffit de montrer que $P \Rightarrow Q, Q \Rightarrow R$ et $R \Rightarrow P.$
$\bullet$ Pour faire un raisonnement par l’absurde pour démontrer que l’assertion $P$ est vraie, on suppose l’assertion $\text{non} \left( P \right)$ vraie et en poursuivant le raisonnement, on arrive à $\text{non} \left( P \right)$ est fausse. On dit que l’on a obtenu une contradiction, donc on conclut que $P$ est vraie.

Voici une liste (non exhaustive) où l’on pourra faire des raisonnements par équivalence :
$\bullet$ lorsque l’on résout une équation ou un système d’équations,
$\bullet$ lorsque l’on cherche l’ensemble de définition d’une fonction.

Exemple : Dire si l’assertion suivante est vraie ou fausse. Donner sa négation.
$\exists M \in \mathbb{R}, \; \forall x \in \mathbb{R}, \; x \le M.$

Réponse :

Cette assertion est fausse. En effet, si l’on prend $x = M + 1,$ on a $x >M.$ L’ordre des quantificateurs est important : ici $\exists M$ est placé avant $\forall x$ … La négation de cette assertion est :

$\forall M \in \mathbb{R}, \; \exists x \in \mathbb{R}, \; x > M.$

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

2. Applications

Méthode 4 : Ne pas se tromper lorsque l’on compose deux applications :

La composition est une nouvelle opération sur les applications. Soient trois ensembles non vides $E, F$ et $G$ et soient deux applications $f: F \to G$ et $g : E \to F.$ On définit l’application $f \circ g: E \to G$ par :

$\forall x \in E, \; f \circ g \left( x \right) = f \left( g \left( x \right) \right) .$

Exemple : Soient $f : \mathbb {R} \to \mathbb{R}$ définie par $f \left(x \right) = e^{x + 1}$ et $g : \mathbb R_+^* \to \mathbb R$ définie par $g \left( x \right) = \ln \left( x \right).$

Déterminer l’ensemble de définition de $f \circ g$ et la calculer si cela est possible.

Réponse :

$\mathbb R$ et pour tout $x \in \mathbb R,$ $\left( f \circ g \right) \left( x \right) = x - 1.$

Méthode 5 : Bijectivité :

$\bullet$ Pour montrer qu’une application est bijective, on montre qu’elle est injective et surjective. Les méthodes ci-dessus s’appliquent donc.

$\bullet$ Pour démontrer que $f$ est une bijection de $E$ sur $F,$ on peut aussi démontrer que, pour tout $y \in F,$ il existe un unique $x \in E$ tel que $y = f \left( x \right).$

$\bullet$ Dans le cas d’une fonction définie sur un intervalle $I$ de $\mathbb R,$ il suffit d’appliquer le théorème de la bijection : on prouve que $f$ est strictement monotone, continue sur l’intervalle $I.$ Alors $f$ est une bijection de $I$ sur $f \left( I \right).$

A ce titre, rappelons que :

$\star$ si $I = \left[ a , b \right]$ et si $f$ est croissante sur $I,$ $f \left( I \right) = \left[ f \left( a \right) , f \left( b \right) \right]$ et si $f$ est décroissante sur $I,$ $f \left( I \right) = \left[ f \left( b \right) , f \left( a \right) \right].$

Exemple : Soit $f : \mathbb R^2 \to \mathbb R^2$ définie par $f \left( x, y \right) = \left( x + y , x - y \right).$

$f$ est-elle bijective ?

Réponse :

On montre que $f$ est injective puis surjective.

$\bullet$ Injectivité:
On se donne deux couples de réels $\left( x , y \right)$ et $\left( x' , y' \right)$ tels que $f \left( x , y \right) = f \left( x' , y' \right).$ On montre que $x=x'$ et $y=y'.$
Comme $f \left( x , y \right) = f \left( x' , y' \right),$ on récupère le système d’équations suivant :

$\begin{cases} x + y =x' + y' \\ x-y = x' - y' \end{cases}.$

La somme de ces deux lignes donne

$2 x= 2 x'$ puis

$x=x'.$ Ensuite, on déduit

$y=y'.$

$f$ est bien injective.

$\bullet$ Surjectivité:

On se donne $\left( a , b \right) \in \mathbb {R}^2,$ on cherche $\left( x , y \right) \in \mathbb {R}^2$ tel que $\left( a, b \right) = f \left( x , y \right).$ On a donc le système suivant :

$\begin{cases} x + y =a \\ x-y = b \end{cases}.$

En sommant ces deux lignes, on a

$2 x=a + b$ puis

$x = \frac{a + b}{2}.$ Ensuite

$y = \frac{a - b}{2}.$ Etant donné que l’on a raisonné par condition nécessaire (on n’a pas fait de raisonnement par équivalence), il faut vérifier que

$f \left( x, y \right) = \left( a , b \right).$
La vérification est facile,

$f$ est bien surjective.

On a montré que

$f$ est injective et surjective, elle est donc bijective.

3. Récurrence

Méthode 6 : Récurrence simple :

Une récurrence s’articule autour de quatre étapes principales :
$\bullet$ On énonce proprement la proposition que l’on veut montrer.
$\bullet$ On initialise en montrant que $\mathcal P_{n_0}$ est vraie, en général on montre que la proposition est vraie lorsque $n$ est égal à $0$ ou $1.$
$\bullet$ En supposant la propriété vraie au rang $n,$ il faut montrer que la propriété est vraie au rang $n + 1.$ C’est l’hérédité.
$\bullet$ La conclusion.

Exemple : Montrer que pour tout $n \in \mathbb N,$ on a

$\sum_{k=0}^n k^2 = \frac{n \left( n+ 1 \right) \left( 2 n + 1 \right)}{6}.$

Réponse : On présente la récurrence comme suit :
$\bullet$ On introduit la proposition pour $n \in \mathbb N,$ $\mathcal P_n : "\sum_{k=0}^n k^2 = \frac{n \left( n+ 1 \right) \left( 2 n + 1 \right)}{6} ".$
$\bullet$ $\mathcal P_0$ est manifestement vraie, car $0=0.$
$\bullet$ On suppose que $\mathcal P_n$ est vraie pour un certain entier $n$ fix\’e. Montrons que $\mathcal P_{n +1}$ est vraie, c’est-à-dire, montrons que

$\sum_{k=0}^{n + 1} k^2 = \frac{ \left( n + 1 \right) \left( n+ 2 \right) \left( 2 n + 3 \right)}{6}.$

On a donc

$\begin{eqnarray*}\sum_{k=0}^{n + 1} k^2 &=& \sum_{k=0}^{n} k^2 + \left( n + 1 \right) ^2 \\&=& \frac{n \left( n+ 1 \right) \left( 2 n + 1 \right)}{6} +\left( n + 1 \right) ^2 (HR)\\&=& \frac{n \left( n+ 1 \right) \left( 2 n + 1 \right) + 6 \left( n + 1 \right)^2}{6} \\&=& \frac{\left( n + 1 \right) \left( n \left( 2 n + 1 \right) + 6 \left( n + 1 \right) \right)}{6} \\&=& \frac{\left( n + 1 \right) \left( 2n^2 + 7n + 6 \right)}{6} \\&=& \frac{\left( n + 1 \right) \left( n + 2 \right) \left( 2 n + 3 \right)}{6}.\end{eqnarray*}$

$\bullet$ Par le principe de raisonnement par récurrence, la proposition

$\mathcal P_n$ est vraie pour tout entier naturel

$n.$

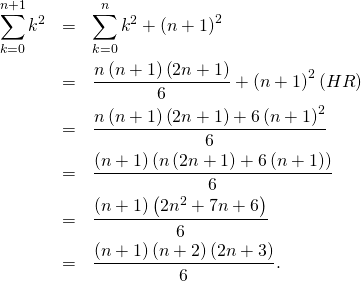
Méthode 7 : Récurrence forte :

La récurrence forte sert lorsque l’on a besoin de $\mathcal P_{n_0}, \mathcal P_{n_0 +1}, \cdots , \mathcal P_n$ pour montrer $\mathcal P_{n + 1}.$
$\bullet$ On énonce la proposition que l’on veut montrer.
$\bullet$ On initialise en montrant que $\mathcal P_{n_0}$ est vraie. En général, on montre que $\mathcal P_0$ est vraie.
$\bullet$ En supposant $\mathcal P_{n_0}, \mathcal P_{n_0 + 1} , \cdots , \mathcal P_n$ vraies, on montre que $\mathcal P_{n+ 1}$ est vraie.
$\bullet$ La conclusion.

Exemple :

Soit la suite $\left( u_n \right)_{n \in \mathbb N^*}$ définie par $u_1=2$ et pour tout $n \in \mathbb N^*,$

$u_{n + 1} = \frac{2}{n} \sum_{k=1}^n u_k .$

Montrer que pour tout $n \in \mathbb N,$ $u_n = 2n.$

Réponse : On procède par récurrence forte.
$\bullet$ Pour tout $n \in \mathbb {N}^*,$ on pose $\mathcal P_n$ : « $u_n = 2n$ « .
$\bullet$ $u_1 = 2 = 2 \times 1$ donc $\mathcal P_1$ est vraie.
$\bullet$ On suppose $\mathcal P_1, \mathcal P_2, \cdots , \mathcal P_n$ vraies et montrons que $\mathcal P_{n + 1}$ est vraie. On a

$\begin{eqnarray*}u_{n + 1} &=& \frac{2}{n} \sum_{k=1}^n u_k \\&=& \frac{2}{n} \sum_{k=1}^n 2 k \qquad \text{(HR)} \\&=& \frac{4}{n} \times \frac{n \left( n + 1 \right)}{2} \\&=& 2 \left( n + 1 \right).\end{eqnarray*}$

$\bullet$ Par le principe de raisonnement par récurrence, la proposition

$\mathcal P_n$ est vraie pour tout entier naturel

$n.$

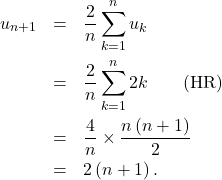
UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

4. Calcul de sommes et produits

Méthode 8 : Les sommes classiques :

Nous les rappelons ci-dessous (les lettres $a$ et $b$ désignent des réels et $x \in \mathbb R$ ) :
1) $\sum_{k=0}^n \binom{n}{k} a^k b^{n - k} = \left( a + b \right)^n,$ c’est la formule du binôme de Newton,
2) $\sum_{k=0}^n k = \frac{n \left( n + 1 \right)}{2}$
3) $\sum_{k=0}^n k^2 = \frac{n \left( n+ 1 \right) \left( 2 n +1 \right)}{6}$ ,
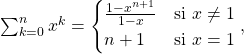4) $\sum_{k=0}^n x^k= \begin{cases} \frac{1 - x^{n + 1}}{1 - x} & \text{si } x \neq 1 \\ n + 1 & \text{si } x= 1 \end{cases},$ formule de la somme des termes d’une suite géométrique. Cette formule est encore valable pour $x \in \mathbb C.$
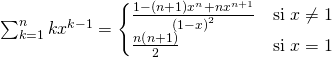5) $\sum_{k=1}^n k x^{k - 1} = \begin{cases} \frac{1- \left( n + 1 \right) x^n + n x^{n + 1}}{\left( 1 - x \right)^2} & \text{si} \; x \neq 1 \\ \frac{n \left(n + 1 \right)}{2} & \text{si} \; x = 1 \end{cases}$ , formule obtenue en dérivant celle de la somme des termes d’une suite géométrique (à ne pas retenir par coeur !) Cette formule est encore valable pour $x \in \mathbb C.$

Exemple :

Soit $n \in \mathbb N^*,$

Que vaut $\sum_{k=1}^n \binom{n}{k - 1} 2^k$ ?

Réponse :

Cela ressemble à un binôme de Newton ! La présence du $k- 1$ dans le coefficient binomial nous invite à faire le changement d’indice $i= k- 1.$ Ainsi

$S_2 = \sum_{i=0}^{n - 1} \binom{n }{i} 2^{i + 1}.$

Pour appliquer la formule du binôme, il faut que la somme se termine à $n$ et que le $2$ soit seulement à la puissance $i,$ d’où en faisant ces petits changements :

$S_2 = 2 \sum_{i=0}^{n - 1} \binom{n }{i} 2^{i }$
= $2 \left( \sum_{i=0}^{n } \binom{n }{i} 2^{i } - \binom{n }{n} 2^{n } \right)$

= $2 \left( \left( 2 + 1 \right)^n - 2^n \right)$

$2 \left( 3^n - 2^n \right).$

Méthode 9 : Les sommes télescopiques :

Cette méthode permet de simplifier facilement les sommes qui peuvent se mettre sous la forme $\sum_{k=p}^n \left( a_{k + 1} - a_k \right).$ En effet, on a

$\sum_{k=p}^n \left( a_{k + 1} - a_k \right) = a_{n + 1} - a_p.$

Exemple : Soit $n \in \mathbb N^*,$

Que vaut $\sum_{k=1}^n \left( \sqrt{k +1} -\sqrt{k} \right)$ ?

Réponse : $\sqrt{n + 1} - 1$

Méthode 10 : Les sommes doubles :

Pour calculer des sommes doubles $\sum_{i=1}^n \sum_{j=1}^p a_{ij},$ l’idée est de calculer en fixant $i$ la quantité $\sum_{j=1}^n a_{ij},$ puis de sommer les résultats ainsi obtenus.

Exemple :

Soit $n \in \mathbb N^*,$

Que vaut $\sum_{i=1}^n \sum_{j=1}^n \min \left( i , j \right)$ ?

Réponse : $\dfrac{n \left( n + 1 \right) \left( 2 n + 1 \right)}{6}$

Pour garder un bon niveau de mathématiques en ECG1, il est essentiel d’effectuer des révisions régulières, aidez-vous alors des cours en ligne suivants :

Cours : Raisonnement et vocabulaire ensembliste

Résumé de cours et méthodes – Raisonnement et vocabulaire ensembliste

1. Quantificateurs, ensemble, logique et raisonnement

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

2. Applications

3. Récurrence

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

4. Calcul de sommes et produits

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Cours : Raisonnement et vocabulaire ensembliste

Résumé de cours et méthodes – Raisonnement et vocabulaire ensembliste

1. Quantificateurs, ensemble, logique et raisonnement

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour réussir sa scolarité

En ligne ou à domicile

2. Applications

3. Récurrence

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension clés de la réussite

Cours de maths en ligne ou à domicile

4. Calcul de sommes et produits

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Les meilleurs profs de maths pour
réussir sa scolarité

La pratique et la compréhension
clés de la réussite