Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Séries numériques en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Résumé de cours et méthodes – Séries numériques
Méthode 1 : Plan d’étude des séries à termes positifs.
Soit ![]() une suite positive et on s’intéresse à la nature de la série
une suite positive et on s’intéresse à la nature de la série ![]() On peut essayer de suivre dans l’ordre les idées suivantes :
On peut essayer de suivre dans l’ordre les idées suivantes :
![]() Un cas simple mais rarement utilisable si
Un cas simple mais rarement utilisable si ![]() ne converge pas vers
ne converge pas vers ![]() alors la série
alors la série ![]() diverge grossièrement.
diverge grossièrement.
![]() Si nécessaire, on détermine un équivalent simple de
Si nécessaire, on détermine un équivalent simple de ![]() disons
disons ![]() On sait que
On sait que ![]() converge si, et seulement si,
converge si, et seulement si, ![]() converge.
converge.
![]()
![]()
![]() est-elle proportionnelle à une série de Riemann ? On rappelle que la série
est-elle proportionnelle à une série de Riemann ? On rappelle que la série ![]() converge si, et seulement si,
converge si, et seulement si, ![]()
![]()
![]()
![]() est-elle proportionnelle à une série géométrique ? On rappelle que
est-elle proportionnelle à une série géométrique ? On rappelle que ![]() converge si, et seulement si,
converge si, et seulement si, ![]()
![]() On peut aussi essayer de raisonner par inégalité en déterminant
On peut aussi essayer de raisonner par inégalité en déterminant ![]() telle que pour
telle que pour ![]() assez grand,
assez grand, ![]() Si
Si ![]() converge, alors
converge, alors ![]() converge.
converge.
Si l’on trouve ![]() tel que pour
tel que pour ![]() assez grand
assez grand ![]() et
et ![]() diverge, alors
diverge, alors ![]() diverge.
diverge.
![]() Si l’on trouve
Si l’on trouve ![]() tel que
tel que ![]() alors
alors ![]() converge.
converge.
En particulier si ![]() contient une exponentielle, on peut chercher si
contient une exponentielle, on peut chercher si ![]()
![]() Si l’on trouve
Si l’on trouve ![]() tel que
tel que ![]() alors
alors ![]() diverge.
diverge.
Piège : ![]() On le dit une fois pour toutes, montrer que
On le dit une fois pour toutes, montrer que ![]() ne prouve rien sur la nature de la série
ne prouve rien sur la nature de la série ![]() . Cela dit juste que la série
. Cela dit juste que la série ![]() ne diverge pas grossièrement mais il y a encore du travail pour montrer la convergence ou la divergence.
ne diverge pas grossièrement mais il y a encore du travail pour montrer la convergence ou la divergence.
![]() Attention à ne pas écrire
Attention à ne pas écrire ![]() sans avoir montré la convergence de la série. Cela n’aurait pas de sens !
sans avoir montré la convergence de la série. Cela n’aurait pas de sens !
Exemple : Etudier la nature des séries dont les termes généraux sont donnés ci-dessous :
1) ![]()
2) ![]()
Réponse : 1) On a ![]() Or la série
Or la série ![]() converge car c’est une série de Riemann. Comme
converge car c’est une série de Riemann. Comme ![]() et
et ![]() sont de même signe, on en déduit que la série
sont de même signe, on en déduit que la série ![]() converge.
converge.
2) On remarque que ![]() donc
donc ![]() Comme
Comme ![]() en posant
en posant ![]() on a
on a ![]() Donc
Donc
![]()
![]()
![]()
![]() .
.
Comme ![]() converge (Riemann) et que
converge (Riemann) et que ![]() et
et ![]() sont de même signe, on en déduit que la série
sont de même signe, on en déduit que la série ![]() converge.
converge.
Les notions liés aux séries numérique peuvent sembler complexes pour certains étudiants en ECG1, mais l’accompagnement en cours de maths à domicile peut s’avérer bénéfique.
Méthode 2 : Plan d’étude des séries à signe quelconque.
Mauvaise nouvelle pour vous, il n’y a pas beaucoup de résultat en ce sens dans votre programme… Le seul résultat est le suivant :
Si la série est absolument convergente (c’est-à-dire que la série ![]() converge), alors la série converge.
converge), alors la série converge.
Piège : Si ![]() et
et ![]() sont deux suites telles que
sont deux suites telles que ![]() et si la série
et si la série ![]() converge, alors la série
converge, alors la série ![]() ne converge pas, à priori. Ce résultat est vrai si l’on suppose les suites de signe constant.
ne converge pas, à priori. Ce résultat est vrai si l’on suppose les suites de signe constant.
Attention à ne pas l’utiliser lorsque les deux suites ne sont pas de signe constant.
Méthode 3 : Calculer la somme d’une série.
Il est indispensable de parfaitement connaître la somme des séries usuelles. Les voici :
![]()
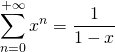 valable pour tout complexe
valable pour tout complexe ![]() tel que
tel que ![]()
![]()
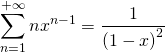 valable pour tout réel
valable pour tout réel ![]()
![]()
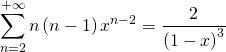 valable pour tout réel
valable pour tout réel ![]()
![]()
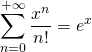 valable pour tout réel
valable pour tout réel ![]()
Le principe est assez simple, il faut jongler avec ces différentes formules. Citons cependant, en vrac, d’autres méthodes pouvant servir :
![]() faire apparaître une somme télescopique,
faire apparaître une somme télescopique,
![]() utiliser un changement d’indice ou se ramener aux séries précédentes.
utiliser un changement d’indice ou se ramener aux séries précédentes.
Exemple : Calculer les sommes suivantes (après avoir montré la convergence de la série) :
1) 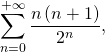
2) 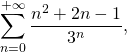
Réponse :
1) Si l’on remarque que : ![]() alors
alors
![]()
Comme les séries ![]() et
et ![]() convergent (c’est du cours !),
convergent (c’est du cours !), ![]() converge. De plus, il est facile de calculer sa somme :
converge. De plus, il est facile de calculer sa somme :
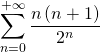
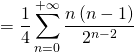
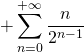
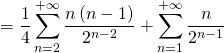
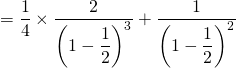
![]()
où dans la deuxième ligne, on a supprimé les termes nuls pour se ramener à des sommes connues.
2) Grâce aux croissances comparées, on peut voir que ![]() car
car ![]() donc
donc ![]() converge.
converge.
Pour le calcul de la somme, on peut voir que ![]() cela permet d’écrire (on vérifie à chaque introduction de somme de série, que l’on manipule une série convergente) :
cela permet d’écrire (on vérifie à chaque introduction de somme de série, que l’on manipule une série convergente) :
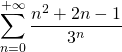
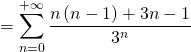

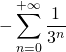
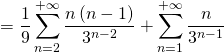
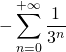
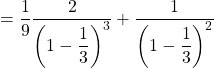
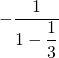
Méthode 4 : Faire une comparaison série-intégrale.
Cette méthode est très utile lorsque l’on demande donner un équivalent d’une somme (par exemple, donner un équivalent de 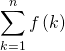 quand
quand ![]() tend vers
tend vers ![]() ). Pour cela, on procède comme suit :
). Pour cela, on procède comme suit :
![]() On s’assure que la fonction
On s’assure que la fonction ![]() est décroissante sur
est décroissante sur ![]() (à minima, on s’assure qu’elle est décroissante sur
(à minima, on s’assure qu’elle est décroissante sur ![]() avec
avec ![]() ),
),
![]() Si
Si ![]() on écrit (
on écrit (![]() étant décroissante) que :
étant décroissante) que :
![]()
![]() On intègre la relation précédente entre
On intègre la relation précédente entre ![]() et
et ![]() pour obtenir :
pour obtenir :
![]()
![]()
![]()
soit :
![]()
En remplaçant ![]() par
par ![]() on récupère :
on récupère :
![]()
Puis en regroupant les deux inégalités :
![]()
Puis en sommant entre ![]() et
et ![]() il vient que :
il vient que :
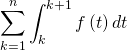


Puis en utilisant la relation de Chasles :
![]()

![]()
Le calcul des intégrales de gauche et de droite fournira souvent un équivalent de 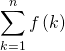 quand
quand ![]() tend vers
tend vers ![]() .
.
Remarque : Ce résultat n’est pas à apprendre par cœur mais à savoir retrouver rapidement. De plus, il faut savoir l’adapter en problème (il faut peut-être sommer de ![]() à
à ![]() par exemple).
par exemple).
Exemple :
Donner un équivalent de 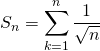 quand
quand ![]() tend vers
tend vers ![]()
Réponse :
Soit ![]() définie par
définie par ![]() Il est clair que
Il est clair que ![]() est décroissante sur
est décroissante sur ![]() On applique la relation de la méthode précédente en se limitant à une somme pour
On applique la relation de la méthode précédente en se limitant à une somme pour ![]() entre
entre ![]() et
et ![]() (si l’on ne s’en souvient pas, pas de panique, on la retrouve !) pour avoir :
(si l’on ne s’en souvient pas, pas de panique, on la retrouve !) pour avoir :
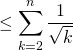
Comme
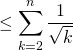
Pour faire apparaître
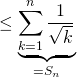
Il semble que
Comme
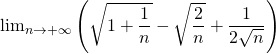
![]()
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Poursuivez vos efforts et gardez le bon cap dans vos révisons en vous aidant des nombreux autres cours en ligne de maths au programme d’ECG1 :

