Chapitres Maths en ECG1

Cours en ligne Maths en ECG1

Chapitres Maths en ECG1

Cours : Suites réelles en ECG1

Résumé de cours Exercices Corrigés

Cours en ligne de Maths en ECG1

Résumé de cours et méthodes – Suites réelles

1. Suites croissantes/décroissantes.

Méthode 1 : Suites convergentes et calcul de la limite de variation d’une suite

Pour montrer la monotonie d’une suite $\left( u_n \right)_{n \in \mathbb {N}},$ on peut étudier le signe de $u_{n + 1} - u_n$ : si le résultat est positif pour tout $n,$ alors la suite est croissante, si le résultat est négatif pour tout $n,$ alors la suite est décroissante.

Pour les suites à valeurs strictement positives, une autre possibilité est de comparer $\dfrac{u_{n + 1}}{u_n}$ et $1.$ Si pour tout $n,$ $\dfrac{u_{n + 1}}{u_n} \ge 1,$ alors la suite est croissante et si pour tout $n,$ $\dfrac{u_{n + 1}}{u_n} \le 1,$ elle est décroissante. Cette méthode sera bien adaptée si la définition de $u_n$ contient « des produits ».

Retrouvez nos profs de maths sur notre plateforme dédié à votre réussite scolaire en ECG1.

Exemple : Soient la suite $\left( u_n \right)_{n \in \mathbb{N}}$ définie par $u_n = \int_0^{\pi / 2} \cos^n \left( t \right) dt.$

Montrer que $\left( u_n \right)_{n \in \mathbb{N}}$ est décroissante.

Réponse :

On a
$u_{n+ 1} - u_n$

= $\int_0^{\pi / 2} \left( \cos^{n+ 1} \left( t \right) - \cos^n \left( t \right) \right) dt$

= $\int_0^{\pi / 2} \cos^n \left( t \right) \left( \cos \left( t \right) - 1 \right) dt \le 0,$

En effet sur $\left[ 0 , \pi / 2 \right],$ $\cos^n \left( t \right) \ge 0$ et $1 - \cos \left( t \right) \le 0,$

Donc on intègre une fonction négative, il s’ensuit que $\left( u_n \right)_{n \in \mathbb{N}}$ est décroissante.

Méthode 2 : Sens de variation d’une suite

Cette méthode est à réserver pour les suites de la forme $u_n = f\left( n \right).$ Auquel cas, si la fonction $f$ est croissante sur $\left[ 0 , +\infty \right[,$ alors la suite $\left( u_n \right)_{n \in \mathbb{N}}$ est croissante et si $f$ est décroissante sur $\left[ 0 , + \infty \right[,$ alors $\left( u_n \right)_{n \in \mathbb{N}}$ est décroissante.

Exemple : Soit la suite $\left( u_n \right)_{n \in \mathbb{N}^*}$ définie par $u_n = \dfrac{\ln n }{n}.$

Réponse : On pose $f \left( x \right) = \dfrac{\ln x}{x}$ pour $x > 0.$

Un rapide calcul donne $f' \left( x \right) = \dfrac{1 - \ln x}{x^2}.$ On a $f' \left( x \right) \ge 0$ si et seulement si $x \ge e.$ Ainsi la suite $\left( u_n \right)_{n \ge 3}$ est croissante.

Méthode 3 : Sens de variation d’une suite

Soit $I$ un intervalle de $\mathbb{R}$ et $f$ une fonction $f : I \to I.$ Soit $\left( u_n \right)_{n \in \mathbb{N}}$ définie par $u_{n + 1} = f \left( u_n \right)$ et $u_0 \in I$ donné.

$\bullet$ Si, pour tout $x \in I,$ on a $f \left( x \right) \le x,$ alors $\left( u_n \right)_{n \in \mathbb{N}}$ est décroissante.

$\bullet$ Si, pour tout $x \in I,$ $f \left( x \right) \ge x,$ alors $\left( u_n \right)_{n \in \mathbb{N}}$ est croissante.

Important : Il faut vérifier que l’intervalle $I$ est stable par $f,$ i.e. que pour tout $x \in I,$ $f \left( x \right) \in I.$

Exemple : Soit la suite $\left( u_n \right)_{n \in \mathbb{N}}$ définie par $u_{n + 1} = e^{u_n} - 1$ et $u_0 = 0.$ Quel est son sens de variation ?

Réponse :

Posons $f \left( x \right) = e^x - 1$ et $g \left( x \right) = f \left( x \right) - x.$ $f$ est une fonction définie sur $I= \mathbb{R}$ à valeurs dans $I$ .

L’étude du signe de $g'$ ( $g ' \left( x \right) = e^x - 1$ ) donne le tableau de variation suivant

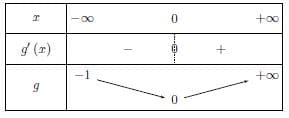
Ainsi pour tout $x \in \mathbb{R},$ on a $f \left( x \right) \ge x$ et donc $\left( u_n \right)_{n \in \mathbb{N}}$ est croissante.

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

Avis Google France ★★★★★ 4,8 sur 5

2. Suites majorées, minorées, bornées.

Méthode 4 : Trouver un majorant/minorant explicitement.

Un calcul direct suffit en général si l’on propose un majorant ou un minorant. Sinon, à vous de conjecturer ce majorant/minorant

Exemple : Montrer que la suite dont le terme général est défini par $u_n = \dfrac{3n +1}{ n +1}$ est majorée par $3.$

Réponse :

On a pour tout $n \in \mathbb{N}$

$u_n - 3 = \dfrac{-2}{n + 1} \le 0.$

Méthode 5 : Justifier un majorant/minorant en faisant un raisonnement par récurrence.

Cette méthode fonctionnera particulièrement bien pour les suites définies par récurrence.

Exemple :

Soit la suite $u$ définie par $u_{n + 1 } = \sin \left( u_n \right)$ et $u_0 = 1.$

Montrer que, pour tout entier $n \in \mathbb{N},$ $0 \le u_n \le 1.$

Réponse :

Procédons par récurrence.

Introduisons, pour $n \in \mathbb{N}$ la proposition $\mathcal P \left( n \right) : " 0 \le u_n \le 1 ".$

$\mathcal P \left( 0 \right)$ est manifestement vraie.

Supposons que $\mathcal P \left( n \right)$ est vraie pour un entier $n \in \mathbb{N}$ fixé.

Montrons que $\mathcal P \left( n + 1 \right)$ est vraie.

Par hypothèse, on a $0 \le u_n \le 1.$ Par croissance de la fonction $\sin$ sur $\left[ 0 , 1 \right],$ on a $\sin \left( 0 \right) \le \sin \left( u_n \right) \le \sin 1$ (ne pas oublier cet argument de croissance !) soit

$0 \le u_{n + 1 } \le \sin \left( 1 \right) \le 1.$

La proposition est donc démontrée par récurrence.

3. Suites convergentes et calcul de la limite.

Méthode 6 : Calcul de la limite pour les suites définies explicitement.

Si la suite est définie explicitement, l’existence et le calcul de la limite doivent pouvoir se faire directement, en utilisant les opérations sur les suites convergentes. En particulier, le produit d’une suite bornée par une suite qui converge vers $0$ converge vers $0.$

On n’oubliera pas les croissances comparées ! Les voici : pour tout $\alpha \in \mathbb{R}$ et $\beta > 0,$

$\lim_{n \to +\infty} \dfrac{ \left(\ln n \right)^{\alpha} }{n^{\beta}}= 0 , \lim_{n \to +\infty} \dfrac{n^{\alpha} }{ e^{ \beta n} }=0 \, \text{et}$ $\, \lim_{n \to +\infty} \dfrac{e^{ \alpha n }}{n!} = 0.$

Exemple :

Montrer que la suite

$\left( u_n \right)_{n \in \mathbb{N}}$ définie par

$u_n = \dfrac{\ln n + \left( - 1 \right)^n}{n}$ converge et calculer sa limite.

Réponse : On écrit $u_n = \dfrac{\ln n }{n} + \dfrac{ \left( - 1 \right)^n}{n}.$

On a, par croissance comparée, $\lim_{n \to +\infty} \dfrac{\ln n}{n} = 0$ et $\lim_{n \to +\infty} \dfrac{ \left( - 1 \right)^n}{n}=0$ comme produit d’une suite qui converge vers $0$ par la suite bornée $\left( \left( - 1 \right)^n \right)_{n \in \mathbb{N}^*}.$

La suite $\left( u_n \right)_{n \in \mathbb{N}^*}$ converge vers $0.$

Méthode 7 : Calcul de la limite pour les suites définies par récurrence.

Soit $f : I \to I$ une fonction continue et $u_{n + 1} = f \left( u_n \right)$ avec $u_0 \in I.$ On suppose que l’on a montré que la suite $\left( u_n \right)_{n \in \mathbb{N}}$ converge vers $l$ et que $l \in I.$ Alors $l$ vérifie $l = f \left( l \right).$ Il suffit alors de résoudre cette équation et de choisir parmi les solutions possibles.

Attention, la continuité de $f$ et le fait que $l \in I$ sont essentiels.

Exemple :

Soit la suite $\left( u_n \right)_{n \in \mathbb{N}}$ définie par $u_{n + 1}= \dfrac{u_n}{u_n + 1}$ et $u_0 = 2.$ Montrer que $\left( u_n \right)_{n \in \mathbb{N}}$ converge et calculer sa limite.

Réponse :

On montre par récurrence que $u_n > 0$ (faites-le !). Aussi

$\dfrac{u_{n+ 1 }}{u_n} = \dfrac{1}{u_n +1} \le 1.$

Ainsi $\left( u_n \right)_{n \in \mathbb{N}}$ est décroissante, minorée donc elle converge. On appelle $l$ sa limite, $l \ge 0$ comme limite d’une suite de réels positifs. Comme $x \mapsto \dfrac{x}{x + 1}$ est continue sur $\mathbb{R}_+,$ $l$ vérifie l’équation $l = \dfrac{l}{l+1}$ soit $l=0$ .

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

4. Suites classiques.

Méthode 8 : Etude des suites classiques.

1) Vous devez savoir étudier les suites arithmético-géométriques, c’est-à-dire définies par une relation du type :

il existe $\left( a , b \right) \in \mathbb{R}^2, a \neq 1,$ pour tout $n \in \mathbb{N},$ $u_{n + 1} = a u_n + b.$

On commence par déterminer le réel $C$ tel que $a C + b = C.$

On note ensuite si $n \in \mathbb{N}, w_n = u_n - C.$ On montre que $\left( w_n \right)_{n \in \mathbb{N}}$ est géométrique de raison $a.$ On en déduit $w_n$ puis $u_n = w_n + C.$

2) On peut généraliser ce résultat aux suites de la forme $u_{n + 1} = a u_n + P \left( n \right)$ où $a \neq 1$ et $P$ est une fonction polynôme.

On commence par chercher une solution particulière $\left( v_n \right)_{n \in \mathbb{N}}$ sous la forme $v_n = Q \left( n \right),$ $Q$ étant une fonction polynôme de même degré que $P.$

Puis on pose $w_n = u_n - v_n.$ On montre que la suite $\left( w_n \right)_{n \in \mathbb{N}}$ est géométrique de raison $a.$ On détermine $w_n$ puis $u_n.$

Exemple : Soit la suite $\left( u_n \right)_{n \in \mathbb{N}}$ définie par $u_{n + 1} = 2u_n + n^2 + 1$ et $u_0=1.$ Exprimer $u_n$ en fonction de $n.$

Réponse :

On applique la méthode ci-dessus avec $P \left( n \right) = n^2 + 1.$ On cherche une suite $\left( v_n \right)_{n \in \mathbb{N}}$ solution sous la forme $v_n = Q \left( n \right)$ où $Q$ est un polynôme de degré $2$ (le même que celui que $P$ ) ainsi $v_n = an^2 + b n +c.$

En traduisant $v_{n + 1}= 2 v_n + n^2 +1,$ on a

$a \left( n + 1 \right)^2 + b \left( n + 1 \right) + c$ $=2 \left( an^2 + bn + c \right) + n^2 + 1.$

En identifiant les coefficients devant $n^2, n$ et $1,$ on récupère le système d’équations suivant :

$\begin{cases} a& =2 a + 1 \\ 2 a + b & = 2b \\ a + b +c & = 2c + 1 \end{cases}.$

La résolution donne $a=-1, b=-2, c=-4.$ Pour tout $n \in \mathbb{N},$ $v_n = -n^2 - 2n - 4.$ Il est facile de vérifier que la suite $\left(u_n - v_n \right)_{n \in \mathbb{N}}$ est géométrique de raison $2,$ ainsi on a $u_n - v_n = 2^n \left( u_0 - v_0 \right)$ avec $v_0 = - 4.$ Puis

$u_n = 5 \times 2^n - n^2 - 2n - 4 .$

Le chapitre sur les suites réelles est un classique de maths en prépa HEC, mais il est important d’être parfaitement au point sur tous les autres chapitres de maths du programme, comme :

Cours : Suites réelles en ECG1

Résumé de cours et méthodes – Suites réelles

1. Suites croissantes/décroissantes.

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

2. Suites majorées, minorées, bornées.

3. Suites convergentes et calcul de la limite.

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

4. Suites classiques.

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales