Chapitres de maths en Terminale S2
Cours sur les nombres complexes en Terminale S2
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale S2
Ce résumé de cours proposé aux élèves qui préparent le bac S2 vous permettra de réviser toutes les notions nécessaires sur les nombres complexes.
1. Notation et définition des complexes en terminale S2
Tout nombre complexe possède un affixe noté ![]() et possède une représentation dans une base orthonormale. Ce nombre possède alors des coordonnées cartésiennes et des coordonnées polaires.
et possède une représentation dans une base orthonormale. Ce nombre possède alors des coordonnées cartésiennes et des coordonnées polaires.
Coordonnées cartésiennes d’un nombre complexe
Soit ![]() un repère cartésien (vecteurs fixes) du plan. Alors, tout point
un repère cartésien (vecteurs fixes) du plan. Alors, tout point ![]() d’affixe
d’affixe ![]() est déterminé par le couple
est déterminé par le couple ![]() tels que :
tels que :
![]()
Les réels ![]() sont les coordonnées cartésiennes du point
sont les coordonnées cartésiennes du point ![]() dans la base
dans la base ![]() .
.
Nous adopterons les appellations suivantes : ![]() est appelé partie réelle et
est appelé partie réelle et ![]() partie imaginaire.
partie imaginaire.
Voici l’écriture algébrique du nombre complexe ![]() :
:
![]()
Coordonnées polaires des nombres complexes
Soit un repère orthonormé ![]() :
:
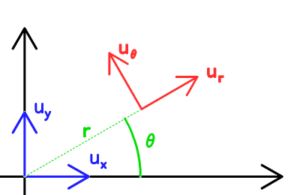
– le vecteur ![]() est un vecteur unitaire dirigé vers le vecteur
est un vecteur unitaire dirigé vers le vecteur ![]() ;
;
– le vecteur orthoradial ![]() est un vecteur unitaire orthogonal au vecteur
est un vecteur unitaire orthogonal au vecteur ![]() , avec un angle de
, avec un angle de ![]() dans le sens anti-horaire.
dans le sens anti-horaire.
Dans ce repère, le point A d’affixe ![]() est décrit par
est décrit par ![]() , avec
, avec ![]() et
et ![]() , tels que :
, tels que :
![]()
Nous pouvons alors écrire la forme trigonométrique du complexe ![]() :
:
![]()
Le nombre ![]() est le module de
est le module de ![]() , noté
, noté ![]() , et le réel
, et le réel ![]() est appelé l’argument de
est appelé l’argument de ![]() .
.
Nous pouvons alors écrire :
![]()
![]()
![]()
Voici la notation exponentielle du complexe :
![]()
![]()
Liens entre les coordonnées cartésiennes et polaires : module et argument
Il est possible de passer des coordonnées cartésiennes aux coordonnées polaires.
![]()
![]() , si
, si ![]()
![]() , si
, si ![]()
![]() , si
, si ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2 – Conjugué, argument et module d’un nombre complexe en terminale S2
L’ensemble des complexes ![]() contient donc l’ensemble des réels
contient donc l’ensemble des réels ![]() . Les lois d’addition et de multiplication s’appliquent dans
. Les lois d’addition et de multiplication s’appliquent dans ![]() .
.
Conjugué d’un nombre complexe
Soit ![]() , dont l’écriture algébrique est
, dont l’écriture algébrique est ![]() , avec
, avec ![]() .
.
Le complexe conjugué de ![]() , noté
, noté ![]() , est défini par:
, est défini par:
![]()
Soient ![]() et
et ![]() deux complexes :
deux complexes :
![]() est un nombre réel si et seulement si sa partie imaginaire est nulle, donc si et seulement si
est un nombre réel si et seulement si sa partie imaginaire est nulle, donc si et seulement si ![]() ;
;
![]() est imaginaire pur si et seulement si sa partie réelle est nulle, donc si et seulement si
est imaginaire pur si et seulement si sa partie réelle est nulle, donc si et seulement si ![]() ;
;
Les points d’affixes ![]() et
et ![]() sont symétriques par rapport à l’axe des abscisses :
sont symétriques par rapport à l’axe des abscisses :
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Si ![]() , alors
, alors ![]() ;
;
Si ![]() , alors
, alors ![]() ;
;
Si ![]() , alors
, alors ![]() .
.
Argument d’un complexe
Soient ![]() et
et ![]() deux nombres complexes non nuls. On note
deux nombres complexes non nuls. On note ![]() l’argument de
l’argument de ![]() .
.
![]() ssi
ssi ![]()
![]() ;
;
![]() est imaginaire pur si et seulement si
est imaginaire pur si et seulement si ![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Module d’un complexe en terminale S2
Soit ![]() . Le module de ce nombre est :
. Le module de ce nombre est :
![]()
Soient ![]() et
et ![]() deux complexes :
deux complexes :
![]() ;
;
![]() si et seulement si
si et seulement si ![]() ;
;
![]()
![]() ;
;
Si ![]() , alors
, alors ![]() ;
;
![]() ;
;
Si ![]() ,
, ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3 – Complexes et équations du second degré en terminale S2
Nous avons plusieurs cas à distinguer dans la résolution des équations du second degré
Cas n°1 : équation ![]() , avec
, avec ![]()
2 cas se présentent à nouveau selon le signe de ![]() .
.
1.1 : ![]()
Si ![]() , alors
, alors ![]() ;
;
Si ![]() , alors
, alors ![]() .
.
Nous avons alors :
![]()
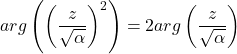
![]()
On en déduit que ![]() .
.
L’équation sur les arguments nous permet de déduire :
![]()
![]() ,
, ![]()
![]() ,
, ![]()
Le nombre ![]() est donc un nombre réel, dont le module vaut
est donc un nombre réel, dont le module vaut ![]() , et l’argument
, et l’argument ![]() ou
ou ![]() (module
(module ![]() ).
).
1.2 : ![]()
Dans ![]() ,
,
![]()
![]()
=![]()
On a donc, ![]() qui est un nombre imaginaire pur, de module
qui est un nombre imaginaire pur, de module ![]() , et d’argument
, et d’argument ![]()
![]() .
.
Cas n°2 : équation ![]() , avec
, avec ![]()
Calculons le discriminant du polynôme : ![]()
Les coefficients ![]() ,
, ![]() et
et ![]() sont réels, nous pouvons donc étudier le signe de
sont réels, nous pouvons donc étudier le signe de ![]() :
:
Si ![]() : le polynôme du 2nd degré admet deux racines réelles différentes :
: le polynôme du 2nd degré admet deux racines réelles différentes :
![]()
![]()
Si ![]() : le polynôme admet une racine réelle double :
: le polynôme admet une racine réelle double : ![]() ;
;
Si ![]() : le polynôme admet 2 racines complexes conjuguées :
: le polynôme admet 2 racines complexes conjuguées :
![]()
![]()
Retrouvez d’autres chapitres à travailler en cours de maths en terminale D :

