Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Variables aléatoires à densité en ECG 1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Ce résumé de cours et de méthodes proposé gratuitement vous fournit toutes les notions à maitriser et des exemples précis sur les variables aléatoires à densité en prépa ECG. Pour aller plus loin, n’hésitez pas à faire appel à un professeur particulier de maths à domicile ou en ligne pour attaquer la deuxième année de prépa ECG sereinement.
1. Généralités sur les variables aléatoires à densité en ECG
Dans ce paragraphe, ![]() est un espace probabilisé.
est un espace probabilisé.
\noindent Une application ![]() de
de ![]() dans
dans ![]() est une variable aléatoire réelle lorsque pour tout
est une variable aléatoire réelle lorsque pour tout ![]()
![]()
On suppose dans ce paragraphe que ![]() n’est ni fini, ni en bijection avec
n’est ni fini, ni en bijection avec ![]()
On définit la fonction de répartition ![]() par si
par si ![]()
![]()
![]()
La fonction de répartition ![]() de
de ![]() vérifie les propriétés suivantes :
vérifie les propriétés suivantes :
![]()
![]() est croissante sur
est croissante sur ![]()
![]()
![]() et
et ![]()
![]()
![]() est continue à droite en tout point
est continue à droite en tout point ![]() et admet une limite à gauche en
et admet une limite à gauche en ![]() égale à
égale à ![]()
![]() Si
Si ![]()
![]()
![]()
![]()
![]() caractérise la loi, c’est-à-dire que deux variables aléatoires
caractérise la loi, c’est-à-dire que deux variables aléatoires ![]() et
et ![]() suivent la même loi si et seulement si
suivent la même loi si et seulement si ![]()
![]() Lorsque
Lorsque ![]() est continue, pour tout
est continue, pour tout ![]()
![]() donc si
donc si ![]()
![]()
![]() et
et ![]()
![]() et
et ![]()
![]()
![]()
![]() Soient
Soient ![]() et
et ![]() deux variables aléatoires définies sur
deux variables aléatoires définies sur ![]() telles que ni
telles que ni ![]() ni
ni ![]() ne soit fini ou en bijection avec
ne soit fini ou en bijection avec ![]() On dit que
On dit que ![]() et
et ![]() sont indépendantes si pour tout
sont indépendantes si pour tout ![]()
![]()
![]()
Cette définition se généralise à ![]() (
(![]()
![]() ) variables aléatoires.
) variables aléatoires.
Méthode 1 : Montrer qu’une fonction est une densité.
![]() Pour montrer qu’une fonction
Pour montrer qu’une fonction ![]() définie sur
définie sur ![]() est une densité sur
est une densité sur ![]() il faut vérifier les deux hypothèses suivantes :
il faut vérifier les deux hypothèses suivantes :
![]()
![]() est continue sur
est continue sur ![]() sauf éventuellement en un nombre fini de points, et à valeurs positives,
sauf éventuellement en un nombre fini de points, et à valeurs positives,
![]() l’intégrale
l’intégrale ![]() converge et est égale à
converge et est égale à ![]()
![]() On se souviendra aussi que la densité caractérise la loi, c’est-à-dire que si deux variables aléatoires ayant respectivement
On se souviendra aussi que la densité caractérise la loi, c’est-à-dire que si deux variables aléatoires ayant respectivement ![]() et
et ![]() pour densité, si
pour densité, si ![]() et
et ![]() sont égales sauf en un nombre fini de points, alors
sont égales sauf en un nombre fini de points, alors ![]() et
et ![]() suivent une même loi.
suivent une même loi.
Exemple : Montrer que les fonctions suivantes sont des densités :
1) ![]() la fonction définie sur
la fonction définie sur ![]() par
par ![]()
![]()
2) Soit ![]()
![]() définie par
définie par 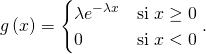
Réponse :
1) Vérifions les deux conditions pour avoir une densité.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 2 : Reconnaître une variable aléatoire à densité et en donner la loi.
Par définition, une variable à densité ![]() est une variable aléatoire telle qu’il existe une densité
est une variable aléatoire telle qu’il existe une densité ![]() telle que pour tout
telle que pour tout ![]()
![]()
![]()
![]() Lorsque l’on connaît la fonction de répartition de la variable
Lorsque l’on connaît la fonction de répartition de la variable ![]() pour montrer que
pour montrer que ![]() admet une densité, on montre que
admet une densité, on montre que ![]() est continue sur
est continue sur ![]() de classe
de classe ![]() sauf éventuellement en un nombre fini de points.
sauf éventuellement en un nombre fini de points.
Si ![]() est de classe
est de classe ![]() en
en ![]()
![]()
![]()
![]() Réciproquement si
Réciproquement si ![]() est une variable aléatoire à densité, sa fonction de répartition
est une variable aléatoire à densité, sa fonction de répartition ![]() est définie par
est définie par
![]()
![]()
La fonction ![]() est continue sur
est continue sur ![]() de classe
de classe ![]() en tout point où
en tout point où ![]() est continue, et en ces points
est continue, et en ces points ![]()
Pour donner la loi d’une variable aléatoire à densité, il suffit au choix de donner
![]()
![]() la fonction de répartition de
la fonction de répartition de ![]()
![]()
![]() une densité
une densité ![]() de
de ![]()
Important : on retiendra que si ![]() est une variable aléatoire à densité, pour tout
est une variable aléatoire à densité, pour tout ![]()
![]()
Piège : Si ![]() est une densité de
est une densité de ![]() toute fonction à valeurs positives égale à
toute fonction à valeurs positives égale à ![]() sauf en un nombre fini de points est aussi une densité de
sauf en un nombre fini de points est aussi une densité de ![]() On ne parle pas de la densité mais d’une densité.
On ne parle pas de la densité mais d’une densité.
Si ![]() est de classe
est de classe ![]() on choisira
on choisira ![]() et on pourra commettre l’abus de langage de parler de la densité de
et on pourra commettre l’abus de langage de parler de la densité de ![]() en choisissant cette densité.
en choisissant cette densité.
Méthode 3 : Calculer la fonction de répartition d’une variable aléatoire  .
.
Il y a deux méthodes selon les données de l’énoncé :
![]() si l’on connaît une densité
si l’on connaît une densité ![]() de
de ![]() on calcule la fonction de répartition de
on calcule la fonction de répartition de ![]() en utilisant
en utilisant ![]()
![]()
Lorsque l’expression de ![]() est définie par raccord sur les intervalles d’extrémités
est définie par raccord sur les intervalles d’extrémités ![]() on calcule
on calcule ![]() en étudiant les différents cas :
en étudiant les différents cas :
![]()
![]() sinon, on revient à la définition :
sinon, on revient à la définition : ![]()
![]() Il est souvent possible de prouver alors que
Il est souvent possible de prouver alors que ![]() admet une densité. Ce sera la méthode à adopter lorsque l’on définira
admet une densité. Ce sera la méthode à adopter lorsque l’on définira ![]() la fonction
la fonction ![]() étant continue sur
étant continue sur ![]() On déterminera la fonction de répartition de
On déterminera la fonction de répartition de ![]() en fonction de celle de
en fonction de celle de ![]() puis on cherchera à prouver que
puis on cherchera à prouver que ![]() admet une densité.
admet une densité.
Exemple :
Soit ![]() une variable aléatoire de fonction de répartition
une variable aléatoire de fonction de répartition ![]() définie par
définie par 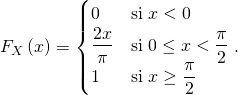
On note ![]()
Trouver la fonction de répartition ![]() de
de ![]() et montrer que
et montrer que ![]() admet une densité que l’on exprimera.
admet une densité que l’on exprimera.
Réponse : La fonction ![]() est continue sur
est continue sur ![]() (on vérifie qu’elle est continue aux points de raccord
(on vérifie qu’elle est continue aux points de raccord ![]() et
et ![]() ),
),
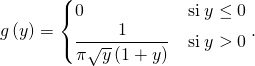
Méthode 4 : Montrer qu’une variable aléatoire à densité admet une espérance.
1) Soit ![]() une variable admettant une densité
une variable admettant une densité ![]() . Pour montrer que
. Pour montrer que ![]() admet une espérance, il faut montrer que l’intégrale
admet une espérance, il faut montrer que l’intégrale ![]() converge absolument.
converge absolument.
Si c’est le cas, on pose ![]()
![]()
2) Si ![]() et
et ![]() sont deux variables aléatoires indépendantes et à densité ayant chacune une espérance, alors la variable aléatoire
sont deux variables aléatoires indépendantes et à densité ayant chacune une espérance, alors la variable aléatoire ![]() admet une espérance et
admet une espérance et
![]()
![]()
Remarque : 1) Lorsque ![]() admet une densité
admet une densité ![]() continue sur
continue sur ![]() et nulle hors de
et nulle hors de ![]() alors
alors ![]() admet une espérance égale à
admet une espérance égale à ![]() puisque les intégrales
puisque les intégrales ![]() et
et ![]() sont absolument convergentes et nulles.
sont absolument convergentes et nulles.
2) Si ![]() est une variable à densité admettant une espérance et si
est une variable à densité admettant une espérance et si ![]()
![]() admet une espérance et
admet une espérance et ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Méthode 5 : Montrer qu’une variable aléatoire à densité admet une variance.
Soit ![]() une variable aléatoire admettant une densité
une variable aléatoire admettant une densité ![]()
Lorsque l’intégrale ![]() converge (elle converge aussi absolument), alors
converge (elle converge aussi absolument), alors ![]() admet une espérance et une variance.
admet une espérance et une variance.
On définit ![]() et la variance de
et la variance de ![]() par :
par :
![]()
![]()
On montre que ![]() et on appelle écart type de
et on appelle écart type de ![]()
![]()
![]()
Remarque : 1) Si ![]() admet une densité continue sur un segment
admet une densité continue sur un segment ![]() et nulle hors de
et nulle hors de ![]() alors
alors ![]() admet une variance car l’intégrale
admet une variance car l’intégrale ![]() est convergente, la fonction
est convergente, la fonction ![]() étant nulle hors de
étant nulle hors de ![]() et dans ce cas
et dans ce cas ![]()
![]() et
et ![]()
![]()
2) Si ![]() est une variable à densité admettant une variance et si
est une variable à densité admettant une variance et si ![]()
![]() admet une variance et
admet une variance et ![]()
![]()
2. Lois de variables à densité usuelles en prepa ECG
Méthode 6 : Sur la loi normale.
La loi normale est une loi assez importante pour faire quelques rappels.
Soient ![]() un réel et
un réel et ![]() un réel strictement positif.
un réel strictement positif.
1) On dit qu’une variable à densité suit une loi normale de paramètres ![]() et
et ![]() si elle admet une densité de la forme
si elle admet une densité de la forme ![]()
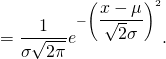
Dans ce cas, on a ![]()
![]() et
et ![]()
![]()
2) Les calculs étant plus simples pour la loi normale centrée réduite (avec ![]() et
et ![]() ), il est bon de savoir que
), il est bon de savoir que
![]() si
si ![]() suit la loi normale de paramètres
suit la loi normale de paramètres ![]() et
et ![]() alors
alors ![]() suit la loi normale centrée, réduite.
suit la loi normale centrée, réduite.
![]() si
si ![]() suit la loi normale centrée, réduite, et si
suit la loi normale centrée, réduite, et si ![]()
![]() suit une loi normale de paramètres
suit une loi normale de paramètres ![]() et
et ![]()
3) Si ![]() est la fonction de répartition de
est la fonction de répartition de ![]() de loi normale de paramètres
de loi normale de paramètres ![]() et
et ![]()
![]()
![]() la fonction
la fonction ![]() ne s’exprime pas à l’aide des fonctions usuelles, mais on peut en calculer les valeurs approchées en utilisant des tables de loi normale ou Scilab et en utilisant les propriétés suivantes :
ne s’exprime pas à l’aide des fonctions usuelles, mais on peut en calculer les valeurs approchées en utilisant des tables de loi normale ou Scilab et en utilisant les propriétés suivantes :
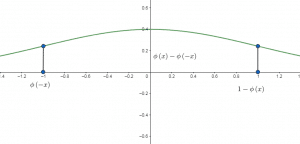
![]()
![]() pour tout
pour tout ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Si vous hésitez, tracez le graphe de la densité 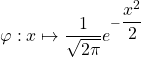 et interprétez les probabilités en termes d’aires de domaine compris entre le graphe de
et interprétez les probabilités en termes d’aires de domaine compris entre le graphe de ![]() et l’axe
et l’axe ![]()
Méthode 7 : Variable aléatoire et loi exponentielle.
La fonction de répartition, une densité de la loi exponentielle sont données par le tableau ci-dessus. Il en est de même de l’espérance et de la variance. Nous citons quelques propriétés qui sont importantes à retenir :
![]() Soit
Soit ![]() est une variable aléatoire admettant une densité.
est une variable aléatoire admettant une densité. ![]() est une variable aléatoire sans mémoire c’est-à-dire vérifiant
est une variable aléatoire sans mémoire c’est-à-dire vérifiant ![]()
![]()
![]()
![]()
si et seulement si ![]() suit une loi exponentielle.
suit une loi exponentielle.
![]() Si
Si ![]()
![]() suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre ![]() si et seulement si
si et seulement si ![]() suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre ![]()
Profitez des autres cours en ligne, exercices, et corrigés d’exercices en ECG1 en maths pour améliorer vos résultats de maths :

