Chapitres Maths en ECG1

Exercices et Corrigés : Espaces vectoriels en ECG1

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices Corrigés

Cours en ligne de Maths en ECG1

Corrigés – Espaces vectoriels et applications linéaires

Exercice 1 :

1) Linéarité :

Pour montrer que $f$ est linéaire, on se donne deux triplets $\left( x_1 , y_1 , z_1 \right), \left( x_2 , y_2 , z_2 \right)$ et un réel $\lambda.$ Montrons que

$f \left( \left( x_1 , y_1 , z_1 \right) + \lambda \left( x_2 , y_2 , z_2 \right) \right)$

$= f \left( x_1 , y_1 , z_1 \right) + \lambda f \left( x_2 , y_2 , z_2 \right).$
Il suffit d’écrire les choses !

$f \left( \left( x_1 , y_1 , z_1 \right) + \lambda \left( x_2 , y_2 , z_2 \right) \right)$ $= f \left( x_1 + \lambda x_2 , y_1 + \lambda y_2 , z_1 + \lambda z_2 \right)$

$= ( x_1 + \lambda x_2 - \left( y_1 + \lambda y_2 \right) - \left( z_1 + \lambda z_2 \right)$

$, y_1 + \lambda y_2 - 2 \left( z_1 + \lambda z_2 \right) )$

$= ( x_1 - y_1 - z_1 + \lambda \left( x_2 - y_2 - z_2 \right)$

$, y_1 - 2 z_1+ \lambda \left( y_2 - 2 z_2 \right) )$

$= \left( x_1 - y_1 - z_1 , y_1 - 2 z_1 \right)$

$+ \lambda \left( x_2 , y_2 - z_2 , y_2 - 2 z_2 \right)$

$= f \left( x_1 , y_1 , z_1 \right) + \lambda f \left( x_2 , y_2 , z_2 \right)$ .

Noyau : Pour trouver le noyau, il faut trouver les triplets

$\left( x, y , z \right)$ tels que

$f \left( x , y , z \right) = \left( 0 , 0 \right).$

$\left( x , y , z \right) \in \mathrm{Ker} \left( f \right)$

$\Leftrightarrow \begin{cases} x - y - z & = 0 \\ y - 2 z& = 0 \end{cases}$

$\Leftrightarrow \begin{cases} y & = 2 z \\ x & = y + z \end{cases}$

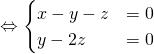
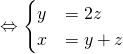
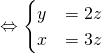$\Leftrightarrow \begin{cases} y & = 2 z \\ x & = 3z \end{cases}$ .Ainsi

$\left( x , y , z \right) = \left( 3 z, 2 z , z \right) = z \left( 3 , 2, 1 \right).$ D’où

$\mathrm{Ker} \left( f \right) = \mathrm{Vect} \left( \left( 3 , 2 , 1 \right) \right).$ En particulier, le noyau est de dimension

$1.$ Image: Le théorème du rang affirme que :

$\dim \mathrm{Ker} \left( f \right) + \dim \mathrm{Im} \left( f \right) = \dim \mathbb{R}^3 = 3.$

Comme $\dim \mathrm{Ker} \left( f \right) = 1,$ on a $\dim \mathrm{Im} \left( f \right) = 2.$ Ainsi $\mathrm{Im} \left( f \right) \subset \mathbb{R}^2$ et $\dim \left( \mathrm{Im} \left( f \right) \right) = \dim \left( \mathbb{R}^2 \right)= 2,$ donc

$\mathrm{Im} \left( f \right) = \mathbb{R}^2. <img src="https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-27b394a2ba7202079390b874a29cd6ae_l3.png" height="159" width="584" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f$ n'étant pas injective, elle n'est pas bijective. <div> 2) Linéarité :Soient $P , Q \in \mathbb{R}_2 \left[ X \right]$ et $\lambda \in \mathbb{R}.$ On a <div style="text-align: justify;">$g \left( P + \lambda Q \right)$ $= ( \left( P + \lambda Q \right) \left( 0 \right) , \left( P + \lambda Q \right) ' \left( 0 \right)$ $, \left( P + \lambda Q \right) '' \left( 0 \right) )$ $= ( P \left( 0 \right) + \lambda Q \left( 0 \right) , P ' \left( 0 \right) + \lambda Q ' \left( 0 \right)$ $ , P '' \left( 0 \right) + \lambda Q '' \left( 0 \right)) $ $= \left( P \left( 0 \right) , P ' \left( 0 \right) , P'' \left( 0 \right) \right)$ $+ \lambda \left( Q \left( 0 \right) , Q ' \left( 0 \right) , Q'' \left( 0 \right) \right) $ $= g \left( P \right) + \lambda g \left( Q \right)$.Noyau : Soit $P \in \mathbb{R}_2 \left[ X \right].\]" title="Rendered by QuickLaTeX.com"/>P \in \mathrm{Ker} \left( g \right)$

si, et seulement si, $P \left( 0 \right) = P ' \left( 0 \right) = P '' \left( 0 \right) = 0.$ Il s’ensuit que $0$ est racine d’ordre au moins $3$ pour $P.$ Comme $\deg P \le 2,$ il s’ensuit que $P = 0.$ On a montré que $\mathrm{Ker} \left( g \right) \subset \left\{ 0 \right\},$ l’inclusion réciproque étant claire, on a bien montré que $\mathrm{Ker} \left( g \right) = \left\{ 0 \right \}.$ Image : On commence par appliquer le théorème du rang :

$\dim \mathrm{Ker} \left( g \right) + \dim \mathrm{Im} \left( g \right) = \dim \mathbb{R}^3 = 3.$

Ainsi $\dim \mathrm{Im} \left( g \right) = 3.$ Finalement $\mathrm{Im} \left( g \right) \subset \mathbb{R}^3$ et $\dim \left( \mathrm{Im} \left( g \right) \right) = \dim \left( \mathbb{R}^3 \right) = 3,$ donc $\mathrm{Im} \left( g \right) = \mathbb{R}^3.$ En particulier, $g$ est bijective.

3) Linéarité :

La linéarité est laissé au lecteur.

Noyau : Soit

$\left( x , y \right) \in \mathbb{R}^2.$

$\left( x , y \right) \in \mathrm{Ker} \left( h \right)$ si, et seulement si,

$h \left( x , y \right) = \left( y , x \right) = \left( 0 , 0 \right).$ Cela est équivalent à

$x = y = 0.$ Ainsi

$\mathrm{Ker} \left( h \right) = \left\{ \left( 0 , 0 \right) \right\}$ et

$h$ est injective.

Image : On commence par appliquer le théorème du rang :

$\dim \mathrm{Ker} \left( h \right) + \dim \mathrm{Im} \left( h \right) = \dim \mathbb{R}^2 = 2.$

Ainsi $\dim \mathrm{Im} \left( h \right) = 2,$ et donc comme ci-dessus $\mathrm{Im} \left( h \right) = \mathbb{R}^2$ et $h$ est surjective.

$h$ est injective et surjective, elle est donc bijective.

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Exercice 2 :

1) Soit $u = \left( x , y , z \right) \in \mathbb{R}^3,$ alors

$f \left( u \right)$ $= f \left( x \left( 1 , 0 , 0 \right) + y \left( 0 , 1, 0 \right) + z \left( 0 , 0 , 1 \right) \right)$
$= x f \left( 1 , 0 , 0 \right) + y f \left( 0 , 1, 0 \right) + z f \left( 0 , 0 , 1 \right)$
$= x \left( 1 , - 1 , 2 \right) + y \left( - 3 , 2 , - 1 \right) + z \left( - 7 , 4, 11 \right)$
$= \left( x - 3 y - 7 z , - x + 2 y + 4 z , 2 x - y + 11 z \right)$

2) $\bullet$ Pour trouver les antécédents éventuels de $\left( - 1 , - 1, 8 \right),$ on résout l’équation $f \left( u \right) = \left( - 1 , - 1, 8 \right).$ On récupère le système

$\begin{cases} x - 3 y - 7 z & = - 1 \\ - x + 2 y + 4 z & = - 1 \\ 2 x - y + 11 z & = 8 \end{cases}.$

La résolution de ce système se fait grâce au pivot de Gauss. On trouve $\left( x , y ,z \right) = \left( 5 , 2 , 0 \right).$

$\bullet$ Pour trouver les antécédents éventuels de

$\left( - 2 , 1 , 3 \right),$ on résout l’équation

$f \left( u \right) = \left( - 1 , - 1, 8 \right).$ On récupère le système

$\begin{cases} x - 3 y - 7 z & = -2 \\ - x + 2 y + 4 z & =1 \\ 2 x - y + 11 z & = 3 \end{cases}.$

La résolution de ce système se fait grâce au pivot de Gauss. On trouve $\left( x , y ,z \right) = \left( - \dfrac35 , \dfrac25 , \dfrac15 \right).$

Injectivité : Pour montrer que

$f$ est injective, montrons que

$\mathrm{Ker} \left( f \right) = \left\{ \left( 0 , 0 , 0 \right) \right\}.$

$\left( x , y, z \right) \in \mathrm{Ker} \left( f \right)$ si, eu seulement si

$f \left( x , y , z \right) = \left( 0 , 0 , 0 \right).$ Cela donne le système:

$\begin{cases} x - 3 y - 7 z & = 0 \\ - x + 2 y + 4 z & =0 \\ 2 x - y + 11 z & = 0 \end{cases}.$

La résolution donne $x = y = z = 0.$ Ainsi $\mathrm{Ker} \left( f \right) \subset \left\{ \left( 0 , 0 , 0 \right) \right\}.$ L’inclusion réciproque étant claire, on a établi que $\mathrm{Ker} \left( f \right) = \left\{ \left( 0, 0 , 0n\right) \right\}$ et $f$ est injective.

Surjectivité : Le théorème du rang donne :

$\dim \mathrm{Ker} \left( f \right) + \dim \mathrm{Im} \left( f \right) = \dim \mathbb{R}^3 = 3.$

Or $\dim \mathrm{Ker} \left( f \right) = 0$ donc $\dim \mathrm{Im} \left( f \right) =3.$ Et, $\mathrm{Im} \left( f \right) \subset \mathbb{R}^3$ et ces deux espaces ont la même dimension, ils sont donc égaux. Donc $f$ est surjective.

En particulier,

$f$ est bijective.

Exercice 3 :

1) Soient $M , N \in \mathcal M_n \left( \mathbb{R} \right)$ et $\lambda \in \mathbb{R}.$ On a :

$\begin{eqnarray*} f \left( M + \lambda N \right) &=& A \left( M + \lambda N \right) \\ &=& AM + \lambda AN \\ &=& f \left( M \right) + \lambda f \left( N \right). \end{eqnarray*}$

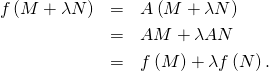
$f$ est donc linéaire.

2) Soit $g : \mathcal M_n \left( \mathbb{R} \right) \to \mathcal M_n \left( \mathbb{R} \right)$ définie par $g \left( M \right) = A^{- 1} M.$

Calculons

$f \circ g.$ Pour

$M \in \mathcal M_n \left( \mathbb{R} \right),$ on a

$\left( f \circ g \right) \left( M \right) = f \left( g \left( M \right) \right) = f \left( A^{-1} M \right) = A A^{- 1} M = M.$

Il s’ensuit que $f \circ g =i d.$ Donc $f$ est bijective et $f^{- 1} =g.$

3) Si

$f$ est surjective alors en particulier la matrice

$I_n$ admet un antécédent par

$f,$ disons

$N \in \mathcal M_n \left( \mathbb{R} \right).$ Ainsi

$f \left( N \right) = M N = I_n .$

Donc $M$ est inversible et $M^{- 1} = N.$

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Exercice 4 :

1) Déjà $E$ est non vide car la suite nulle est bien dans $E.$

Soient

$\left( u_n \right)_{n \in \mathbb{N}}$ et

$\left( v_n \right)_{n \in \mathbb{N}}$ deux suites de

$E$ et

$\lambda \in \mathbb{R}.$ Montrons que la suite

$u + \lambda v \in E.$ Pour tout

$n \in \mathbb{N},$ on a :

$\left( u_{n + 2 } + \lambda v_{n + 2 } \right)$

$= u_{n + 2 } + \lambda v_{n + 2}$

$= 3 u_{n + 1 } - 2 u_n + \lambda \left( 3 v_{n + 1} - 2 v_n \right)$

$= 3 \left( u_{n + 1} + \lambda v_{n + 1} \right) - 2 \left( u_n + \lambda v_n \right)$ .

Il s’ensuit que la suite

$u + \lambda v \in E.$

2) Pour montrer que

$\varphi$ est un isomorphisme, montrons que

$\varphi$ est injective et surjective.

Injectivité :

Soit

$u \in E$ tel que

$\varphi \left( u \right) = \left( u_0 , u_1 \right) = \left( 0 , 0 \right),$ montrons que

$u = 0,$ i.e. montrons que pour tout

$n \in \mathbb{N}, u_n = 0 .$ Pour cela, on procède par récurrence double : on pose

$\mathcal P_n$ : «

$u_n = 0$ « .

$\bullet$

$\mathcal P_0$ et

$\mathcal P_1$ sont vraies, par hypothèse.

$\bullet$ Supposons

$\mathcal P_n$ et

$\mathcal P_{n + 1}$ vraies et montrons que

$\mathcal P_{n + 2}$ est vraie.

Les hypothèses

$\mathcal P_n$ et

$\mathcal P_{n + 1}$ signifient

$u_n = u_{n + 1} = 0.$

Or, on a

$u_{n + 2 } = 3 u_{n + 1 } - 2 u_n = 0,$ d’où

$u_{n + 2 =0}$ et

$\mathcal P_{n + 2}$ est vraie.

$\bullet$ On a bien montré que pour tout

$n \in \mathbb{N}, u_n = 0$ donc

$\varphi$ est injective.

Surjectivité :

Soit

$\left( a , b \right) \in \mathbb{R}^2.$ Pour voir que

$\varphi$ est surjective, soit la suite

$u$ définie par

$u_{n + 2} = 3 u_{n + 2} - 2 u_n$ pour tout

$n \in \mathbb{N}$ et

$u_0 = a$ et

$u_1 = b.$ De sorte que

$\varphi \left( u \right) = \left( u_0 , u_1 \right) = \left( a , b \right).$ Ainsi

$\varphi$ est surjective.

3) Comme

$\varphi$ est un isomorphisme, on a

$\dim \left( E \right) = \dim \left( \mathbb{R}^2 \right) =2.$

4) On procède par analyse-synthèse. Soit

$\left( q^n \right)_{n \in \mathbb{N}}$ (avec

$q \in \mathbb{R}$ ) une suite géométrique de

$E.$ Ainsi, pour tout

$n \in \mathbb{N},$ on a

$q^{n+ 2} = 3 q^{n + 1} - 2 q^n.$

On remarque que

$q= 0$ est une solution possible.

Supposons maintenant

$q \neq 0.$ On simplifie par

$q^n,$ on récupère l’équation

$q^2 = 3q - 2,$ soit

$q^2 - 3 q + 2 = 0.$ Cette équation est simple à résoudre et donne deux solutions

$q = 1$ et

$q = 2.$

Réciproquement, il est simple de vérifier que les suites

$\left( 0 \right)_{n \in \mathbb{N}}, \left( 1 \right)_{n \in \mathbb{N}}$ et

$\left( 2^n \right)_{n \in \mathbb{N}}$ sont bien dans

$E.$

5) On pose les suites

$u$ et

$v$ définies par

$u_n = 1$ et

$v_n = 2^n.$ Montrons que la famille

$\left( u , v \right)$ est libre. On se donne

$a, b \in \mathbb{R}$ tels que

$a u + b v = 0$ et montrons que

$a= b =0.$

La relation

$a u + b v = 0$ signifie que pour tout

$n \in \mathbb{N},$

$a + b \times 2^n = 0.$ En prenant pour valeurs

$n = 0$ et

$n= 1,$ on obtient le système suivant :

$\begin{cases} a + b & = 0 \\ a + 2 b & = 0 \end{cases}.$

La résolution de ce système donne

$a =b = 0.$

La famille

$\left( u , v \right)$ est une famille libre dans un espace vectoriel de dimension

$2,$ c’est donc une base.

On retrouve le résultat portant sur les suites récurrentes linéaires d’ordre

$2.$

Ne restez pas sur vos acquis, et continuez vos révisons et vos entraînements sur les chapitres de maths à suivre au programme d’ECG1 :