Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés : Fonctions réelles à variables réelles en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Fonctions réelles à variables réelles
Exercice 1 :
1) On a une forme indéterminée de la forme ![]() . La présence de
. La présence de ![]() au dénominateur nous fait penser à un taux d’accroissement. Posons
au dénominateur nous fait penser à un taux d’accroissement. Posons ![]() ainsi :
ainsi :
![Rendered by QuickLaTeX.com \[\dfrac{x + \dfrac1x - 2}{x - 1} = \dfrac{f \left( x \right) - f \left( 1 \right)}{x - 1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-800d53cd361662bacf95dd7f07b21688_l3.png)
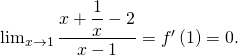
2) Il est classique que ![]() De m\^eme
De m\^eme ![]() Comme
Comme
![]()
on a
![]()
![Rendered by QuickLaTeX.com \[\dfrac{x^2 + e^x}{x^2 + 1} = \dfrac{x^2 \left( 1 + \dfrac{e^x}{x^2} \right)}{x^2 \left( 1 + \dfrac{1}{x^2} \right)} = \dfrac{ 1 + \dfrac{e^x}{x^2} }{1 + \dfrac{1}{x^2} }.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7c0ceeab4915a8cdd5c0a58e169cffa6_l3.png)
5) On s’intéresse d’abord à ![]() En utilisant l’expression conjuguée de
En utilisant l’expression conjuguée de ![]() qui est
qui est ![]() on a :
on a :
Comme
![Rendered by QuickLaTeX.com \[\lim_{x \to + \infty} e^{ \dfrac{1}{\sqrt{x + 1} + \sqrt{x}} } = 1,\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9ecbebfa2d44a6bfdf2abe065755e65e_l3.png)
et
![]()
6) Il y a une puissance, on commence par mettre l’expression sous forme exponentielle, pour ![]() on a :
on a :
ainsi
![]()
Alors, par produit, ![]()
![Rendered by QuickLaTeX.com \[\lim_{x \to 0} e^{\dfrac{\ln \left( 1 + \sin \left( x \right) \right)}{x}} = e.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-72449ecc82cb86769d0c220f37b6c48f_l3.png)
7) Pour ![]() on a
on a
![]()
Or ![]() c’est le taux d’accroissement de la fonction
c’est le taux d’accroissement de la fonction ![]() en
en ![]() et
et ![]() grâce à une croissance comparée. D’où
grâce à une croissance comparée. D’où
![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 :
1) Montrons que ![]()
![]()
2) On forme le taux d’accroissement ![]() En procédant de la même façon que ci-dessus, on montre
En procédant de la même façon que ci-dessus, on montre ![]()
3) Un simple calcul donne, pour ![]()
![]() On a, comme avant,
On a, comme avant, ![]() il suffit donc montrer que
il suffit donc montrer que ![]() n’admet pas de limite en
n’admet pas de limite en ![]()
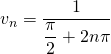 de sorte que
de sorte que Exercice 3 :
Posons ![]() On a
On a ![]() et
et ![]() Comme
Comme ![]() est continue sur
est continue sur ![]() comme différence de deux fonctions continues sur
comme différence de deux fonctions continues sur ![]() , le théorème des valeurs intermédiaires assure qu’il existe
, le théorème des valeurs intermédiaires assure qu’il existe ![]() tel que
tel que ![]() soit
soit ![]()
Exercice 4 :
1) Il est clair que ![]() est continue sur
est continue sur ![]() et
et
2) Pour ![]() on pose
on pose ![]() : «
: « ![]() « .
« .![]() Si l’on prend
Si l’on prend ![]() on a
on a ![]() soit
soit ![]() Ainsi
Ainsi ![]() est vraie.
est vraie.
![]() Supposons
Supposons ![]() vraie, montrons que
vraie, montrons que ![]() vraie. Pour cela, écrivons
vraie. Pour cela, écrivons
![]()
![]()
![]()
![]()
![]() .
.
Ainsi ![]() est donc vraie pour tout
est donc vraie pour tout ![]()
3) Pour ![]()
![]() soit
soit ![]() et
et ![]()
4) Il est facile de montrer par récurrence que pour tout ![]() et pour tout
et pour tout ![]() on a
on a ![]() Ainsi, si
Ainsi, si ![]() et
et ![]() on a
on a
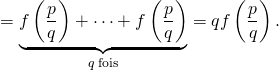
Or,
Par la question 4, on a ![]() Or
Or ![]() De plus,
De plus, ![]() car la fonction
car la fonction ![]() est continue en
est continue en ![]()
6) On vient de montrer que pour tout ![]() on a
on a ![]() Ainsi, les seules fonctions solutions sont les fonctions linéaires.
Ainsi, les seules fonctions solutions sont les fonctions linéaires.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Ne relâchez pas vos efforts et assurez-vous de bien connaître vos cours, en vous exerçant sur les autres exercices des chapitres de maths en ECG1 :

