Chapitres Maths en ECG1
Chapitres Maths en ECG1
Corrigés : Nombres complexes en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Corrigés – Nombres complexes
Exercice 1 :
![]() Il est facile de voir que
Il est facile de voir que ![]()
![]() On a
On a ![]() et
et ![]() d’où
d’où ![]()
![]() On a
On a ![]() et
et ![]() d’où
d’où ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Produit scalaire
1) Mettons ![]() sous forme exponentielle.
sous forme exponentielle.
On a ![]() Ainsi, si l’on pose
Ainsi, si l’on pose ![]() avec
avec ![]() de sorte que
de sorte que ![]() On résout
On résout
![]()
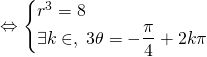
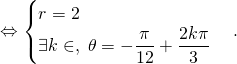
On obtient trois valeurs pour ![]() dans un intervalle de longueur
dans un intervalle de longueur ![]() :
: ![]() et
et ![]() et on obtient trois solutions :
et on obtient trois solutions :
![]()
2) 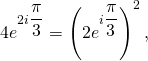 une racine évidente est
une racine évidente est ![]() donc les deux solutions sont
donc les deux solutions sont ![]() et
et ![]()
3) On pose ![]() On a donc la nouvelle équation :
On a donc la nouvelle équation : ![]() Cette équation est facile à résoudre et donne deux solutions :
Cette équation est facile à résoudre et donne deux solutions : ![]() et
et ![]()
L’équation ![]() admet
admet ![]() solutions :
solutions : ![]() et
et ![]() De la même fa\c{c}on, l’équation
De la même fa\c{c}on, l’équation ![]() donne deux solutions :
donne deux solutions : ![]() et
et ![]()
Finalement, l’équation admet ![]() solutions :
solutions : ![]() et
et ![]()
4) On calcule
![]()
![]() Ainsi, il y a deux racines
Ainsi, il y a deux racines ![]() et
et ![]()
5) On a ![]()
![]() .
.
Calculons maintenant les racines carrées de ![]() méthode 6. Soient
méthode 6. Soient ![]() et
et ![]() deux réels tels que
deux réels tels que ![]()
En développant, on a ![]() soit en identifiant les parties réelles et les parties imaginaires :
soit en identifiant les parties réelles et les parties imaginaires :
![Rendered by QuickLaTeX.com \[\begin{cases} a^2 - b^2 & = - 12 \\ ab & = 8 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-38adea933857dbc3dc4e74c9340a6fe5_l3.png)
En utilisant le module dans l’égalité ![]() on récupère
on récupère ![]() On a finalement les relations suivantes :
On a finalement les relations suivantes :
![Rendered by QuickLaTeX.com \[\begin{cases} a^2 - b^2 & = - 12 \\ ab & = 8 \\ a^2 + b^2 & = 20 \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-73bf0ee2b52618456a0a66d6394c74cb_l3.png)
En sommant la première et la troisième ligne, on a ![]() soit
soit ![]() ou
ou ![]() En utilisant la relation
En utilisant la relation ![]() on a
on a ![]() (si
(si ![]() ) ou
) ou ![]() (si
(si ![]() ).
).
Finalement les deux racines carrées de ![]() sont
sont ![]() et
et ![]()
Les racines de l’équation sont donc :
![]() et
et ![]()
Exercice 3 :
On rappelle que les racines ![]() -ièmes de l’unité sont de la forme :
-ièmes de l’unité sont de la forme : ![]() avec
avec ![]()
Somme :
On calcule 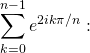
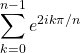
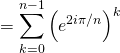
On calcule 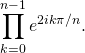
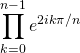
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 4 :
L’inégalité à prouver est équivalente à :
![]()
Pour s’en convaincre, il suffit de remplacer ![]() par
par ![]() Pour prouver cette dernière inégalité, on introduit
Pour prouver cette dernière inégalité, on introduit ![]() le point d’affixe
le point d’affixe ![]() ,
, ![]() le point d’affixe
le point d’affixe ![]() et
et ![]() le point d’affixe
le point d’affixe ![]()
![]() Si
Si ![]() ou
ou ![]() l’inégalité est claire (il y a même égalité).
l’inégalité est claire (il y a même égalité).
![]() On suppose donc
On suppose donc ![]() et
et ![]() Ainsi, l’inégalité à prouver est :
Ainsi, l’inégalité à prouver est :
![]()
Or dans un triangle, la longueur d’un des côtés est inférieure à la somme des longueurs des deux autres côtés, cela prouve l’inégalité précédente et termine l’exercice.
Pour plus d’exercices et corrigés d’exercices de maths en ECG1, rendez-vous sur les autres cours en ligne d’ECG1 :

