Cours en ligne Physique en Maths Sup
Chapitres Physique en MPSI, PCSI, MP2I, PTSI
Exercices corrigés électricité : régime sinusoïdal forcé en maths sup
Résumé de cours Cours en ligne de physique en Maths Sup
L’étude du régime sinusoïdal forcé en électricité représente un volet fondamental dans les programmes des classes préparatoires aux grandes écoles scientifiques en maths sup, offrant une compréhension approfondie des phénomènes électriques soumis à des courants sinusoïdaux forcés et de leurs applications dans divers domaines de la physique appliquée. Si vous rencontrez des difficultés dans ce domaine, n’hésitez pas à envisager des cours particuliers en physique chimie.
Si vous ne parvenez pas à trouver immédiatement le professeur idéal, notre équipe se tiendra à votre disposition pour vous accompagner dans cette recherche. Notre engagement est de vous fournir l’enseignant le mieux adapté à vos besoins spécifiques en électricité.
Exercices corrigés : Imdépances, Quadripôles et Filtrage
Plan des exercices sur le régime sinusoïdal forcé :
A. Impédances
B. Étude de circuits en RSF
C. Étude de résonance
D. Quadripôles et filtrage
COURS EN PREPA MATHS SUP
Les meilleurs professeurs particuliers en CPGE
POUR ACCÉLÉRER MA PROGRESSION EN PRÉPA
Avis Google France ★★★★★ 4,9 sur 5
A. Impédances
Ex. 1 Bouchon.
Un dipôle est qualifié de bouchon s’il se comporte comme un interrupteur ouvert à une certaine fréquence.
1. Quel est le dipôle bouchon à très basse fréquence ?
2. Quel est le dipôle bouchon à très haute fréquence ?
3. Montrer qu’une association bobine-condensateur judicieuse est un bouchon pour une fréquence particulière qu’on exprimera en fonction de ![]() et de
et de ![]()
Correction :
Un dipôle bouchon doit avoir une impédance qui tend vers l’infini pour la fréquence choisie.
1. ![]()
donc un condensateur est un bouchon à très basse fréquence.
2. ![]()
donc une bobine est un bouchon à très haute fréquence.
3. L’association L//C a pour impédance
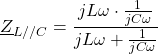
![]()
donc elle tend vers l’infini quand ![]() tend vers la pulsation propre
tend vers la pulsation propre![]()
Ex. 2. Association LC//LC.
1. À partir de deux inductances ![]() et
et ![]() et de deux capacités
et de deux capacités ![]() et
et ![]() , on définit les quatre grandeurs
, on définit les quatre grandeurs
![]()
![]()
![]()
![]()
Que représentent-elles ?
2. On forme un dipôle ![]() en branchant
en branchant ![]() et
et ![]() en série et un dipôle
en série et un dipôle ![]() en branchant
en branchant ![]() et
et ![]() en série. Le dipôle D est l’association parallèle de
en série. Le dipôle D est l’association parallèle de ![]() et de
et de ![]() . Montrer que l’impédance de est nulle ou infini pour
. Montrer que l’impédance de est nulle ou infini pour ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() en précisant les expressions de
en précisant les expressions de ![]() ,
, ![]() et
et ![]()
B. Étude de circuits en RSF
Ex. 1. Circuit simple en RSF.
Dans le circuit suivant, ![]() est associée à
est associée à
![]()
avec ![]() et
et ![]()
et on donne les modules des impédances ![]() ,
, ![]() et
et
![]() . Déterminer
. Déterminer ![]() .
.
![]()
![]() est associée à
est associée à ![]() avec
avec ![]() et
et ![]() et on donne les modules des impédances
et on donne les modules des impédances ![]() ,
, ![]() et
et ![]() . Déterminer
. Déterminer ![]() . » width= »230″ height= »107″ />
. » width= »230″ height= »107″ />
Correction :
On applique le diviseur de tension (ddt) en grandeurs complexes 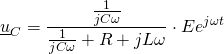
![]()
![]()
![]()
![]()
![]()
donc ![]()
Ex. 2. Circuit R, L C parallèle.
Dans le circuit suivant, ![]() est associée à
est associée à
![]()
avec ![]() et
et ![]()
et on donne les modules des impédances ![]() ,
, ![]() et
et
![]() . Déterminer l’amplitude de
. Déterminer l’amplitude de ![]() .
.
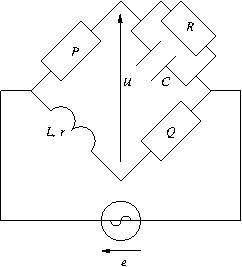
Ex. 3. Pont de Maxwell-Wheatstone.
Dans le circuit
suivant, on cherche à déterminer les caractéristiques de la bobine,
assimilée à l’association série d’une inductance L et d’une résistance r.
On règle les valeurs de R et de C pour que la tension u soit nulle.
Exprimer L et r en fonction de P, Q, R et C.
STAGE INTENSIF MATHS SUP
Profite de tes vacances pour progresser en maths et physique
96% de réussite aux concours
84% dans le TOP 10
99% de recommandation à leurs amis
Avis Google France ★★★★★ 4,9 sur 5
C. Étude de résonance
Ex. 1. Résonance de tension dans un RLC série.
On considère un circuit RLC série alimenté par un générateur de tension alternative sinusoïdale ![]() .
.
On se place en régime sinusoïdal forcé.
1. On pose ![]()
![]() et
et ![]()
Montrer que ![]() et
et ![]() sont sans dimension.
sont sans dimension.
Exprimer ![]() ,
, ![]() et
et ![]()
en fonction de ![]() et
et ![]() .
.
2. Exprimer ![]() en fonction de
en fonction de ![]() ,
, ![]() et
et ![]()
En déduire l’expression de la tension maximale ![]() en fonction de
en fonction de ![]() ,
, ![]() et
et ![]() .
.
3. On pose ![]()
Étudier cette fonction en discutant selon la valeur de ![]() (on se limite à
(on se limite à ![]() positif).
positif).
Commenter en termes de résonance. Conclure.
Correction :
1. Les homogénéités se vérifient par exemple en écrivant que ![]() et
et ![]() sont homogènes à des temps.
sont homogènes à des temps.
On obtient en remplaçant par les expressions ![]()
![]()
![]()
2. Par la loi du diviseur de tension 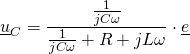
![]()
![]()
En passant aux modules![]()
3. ![]()
On calcule la dérivée ![]()
![]()
Elle a donc le signe de ![]()
Elle s’annulle donc toujours en ![]() .
.
Premier cas : ![]()
![]() est la seule annulation de
est la seule annulation de ![]() ,
, ![]() est strictement décroissante, il n’y a pas de résonance.
est strictement décroissante, il n’y a pas de résonance.
Deuxième cas : ![]()
La dérivée s’annule en ![]() et en
et en ![]()
La fonction présente un maximum en ![]() , et
, et ![]() donc
donc ![]() : c’est une surtension aux bornes du condensateur, il y a résonance.
: c’est une surtension aux bornes du condensateur, il y a résonance.
Ex. 2. Résonance dans un circuit complexe.
On considère le dipôle ci-dessous.
On pose ![]()
![]() et
et ![]()
On en déduit (voir corrigé de l’ex 1) que
![]()
![]()
![]()
1. Exprimer le module Z de son impédance en fonction de ![]() et
et ![]()
2. Montrer que pour certaines valeurs de Q, Z prend une valeur extrémale non nulle.
D. Quadripôles et filtrage
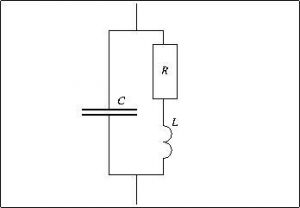
Ex. 1. Quadripôles simples.
1. Déterminer les fonctions de transfert des deux quadripôles suivants sous la forme de fractions rationnelles en ![]() .
.
2. On pose ![]() dans le premier cas,
dans le premier cas, ![]() ,
, ![]() et
et ![]()
dans le second cas, montrer que respectivement
![]()
![]()
3. Dresser les diagrammes de Bode en gain correspondants en prenant ![]() dans le second cas.
dans le second cas.
Ex. 2. Analyse fréquentielle.
Un circuit électrique série ![]() est alimenté par une tension
est alimenté par une tension ![]() périodique de période
périodique de période ![]() . La tension de sortie est la tension aux bornes du résistor.
. La tension de sortie est la tension aux bornes du résistor.
1. Déterminer la fonction de transfert ![]()
2. Dresser le diagramme de Bode en gain. Préciser la nature du filtre et la pulsation de coupure.
3. Le signal d’entrée a une composante continue ![]() .
.
À quelle condition le quadripôle peut-il être considéré comme un moyenneur ?
4. Le signal d’entrée s’écrit
![]()
![]()
où ![]() est une tension électrique donnée et
est une tension électrique donnée et ![]() .
.
Dresser l’allure du spectre en amplitude du signal d’entrée et celle du signal de sortie.
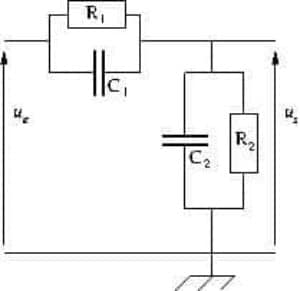
Ex. 3. Quadripôle à deux niveaux d’atténuation.
Dans le quadripôle ci-dessous, on donne ![]() et
et ![]()
On pose ![]() ,
, ![]() et on définit la pulsation réduite
et on définit la pulsation réduite ![]() .
.
On donne le diagramme de Bode asymptotique du quadripôle.
1. Donner l’expression de la fonction de transfert ![]()
en fonction de ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() .
.
2. En donnant l’équivalent à basse et à haute fréquence de ![]() , déterminer les valeurs de
, déterminer les valeurs de ![]() et
et ![]() .
.
3. On envoie en entrée un signal comportant deux composantes harmoniques de fréquences respectives ![]() et
et ![]() , d’amplitudes respectives
, d’amplitudes respectives ![]() et
et ![]() . En expliquant votre raisonnement, tracer l’allure des chronogrammes de
. En expliquant votre raisonnement, tracer l’allure des chronogrammes de ![]() et de
et de ![]() .
.
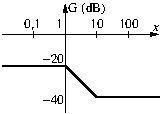
Ex. 4. Filtre de Butterworth [Oral Centrale 2019]
1. Un filtre de Butterworth a pour module de fonction de transfert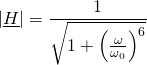
Tracer l’allure de son diagramme de Bode en gain et donner l’intérêt
de ce type de filtre.
2. Justifier qu’un filtre de fonction de transfert ![]()
avec ![]()
est un filtre de Butterworth.
3. À quelle condition sur ![]() le filtre suivant est-il un filtre de Butterworth ?
le filtre suivant est-il un filtre de Butterworth ?
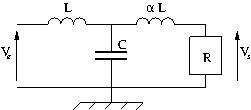
Pour réussir en Maths Sup, il est essentiel de ne pas perdre le rythme de travail ni la motivation. Nos cours en ligne de physique en Maths Sup, sont faits pour vous accompagner et vous aider tout au long de l’année. Jetez donc un œil aux prochains chapitres du programme :
- Exercices sur la mécanique du point maths sup
- Exercice les méthodes énergétiques
- Exercices corrigé maths sup : la loi du moment cinétique
- Exercices : les particules chargées maths sup
- Exercices : les forces centrales maths sup
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut


