Chapitres de maths en Terminale S2
Exercices et corrigés sur la géométrie dans l’espace en Terminale S2
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale S2
N’hésitez pas à consulter et à travailler les exercices corrigés sur la géométrie dans l’espace en terminale S2.
QCM sur la géométrie dans l’espace en terminale S2
Dans le repère orthonormé ![]() de l’espace, on considère les points
de l’espace, on considère les points ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]()
Question 1 :
Le plan ![]() est parallèle
est parallèle
a. au plan ![]()
b. au plan ![]()
c. au plan ![]()
d. aucune des trois propositions proposées ci-dessus n’est correcte.
Question 2 :
Une équation paramétrique de la droite ![]() est
est
a. 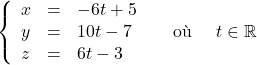
b. 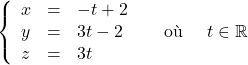
c. 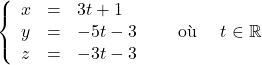
d. aucune des trois propositions proposées ci-dessus n’est correcte.
Question 3 :
Une équation cartésienne du plan passant par ![]() et perpendiculaire à
et perpendiculaire à ![]() est
est
a. ![]()
b. ![]()
c. ![]()
d. aucune des trois propositions proposées ci-dessus n’est correcte.
Exercices distance d’un point à un plan en terminale S2
Soit ![]() le plan d’équation :
le plan d’équation :
![]() :
: ![]()
Question 1 :
Déterminer l’expression analytique de la projection orthogonale ![]() sur le plan
sur le plan ![]() .
.
Question 2 :
Pour tout point ![]() de l’espace, on note
de l’espace, on note ![]() son image par
son image par ![]() .
.
Montrer que pour tout point ![]() ,
, ![]()
Pour tout point ![]() ,
, ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé du QCM de terminale S2 géométrie dans l’espace
Question 1 :
On sait que ![]() \qquad
\qquad ![]() et
et ![]()
De plus ![]() soit
soit ![]()
![]() soit
soit ![]()
![]() soit
soit ![]()
Donc ![]()
Donc ![]()
![]() donc
donc ![]()
![]() donc
donc ![]()
Donc 3 vecteurs du plan ![]() sont normaux à
sont normaux à ![]()
Donc ![]() est normal au plan
est normal au plan ![]()
Donc ![]() est parallèle au plan
est parallèle au plan ![]()
Question 2 :
Les méthodes classiques de détermination d’une équation paramétrique de droite (utiliser l’expression ![]() ou
ou ![]() ) ne conduisent pas à l’une des équations proposées en a. b. ou c.
) ne conduisent pas à l’une des équations proposées en a. b. ou c.
Comme une représentation paramétrique n’est pas unique, nous devons donc tester chaque représentation paramétrique proposée afin de voir si les coordonnées des points ![]() et
et ![]() respectent cette représentation
respectent cette représentation
a. 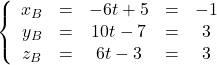
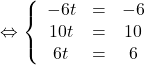
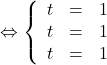 donc
donc ![]() appartient bien à la droite de cette représentation.
appartient bien à la droite de cette représentation.
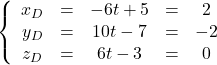
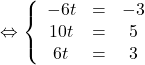
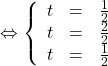 donc
donc ![]() appartient bien à la droite de cette représentation.
appartient bien à la droite de cette représentation.
Question 3 :
Soit ![]() le plan passant par
le plan passant par ![]() et perpendiculaire à
et perpendiculaire à ![]()
On a donc ![]() qui est un vecteur normal à
qui est un vecteur normal à ![]()
Donc l’équation cartésienne de ![]() est de la forme
est de la forme ![]()
Soit ![]()
On sait que ![]()
Donc ![]()
Donc l’équation cartésienne de ![]() est de la forme
est de la forme
![]()
![]()
Corrigé des exercices géométrie dans l’espace
Corrigé de l’exercice la distance d’un point à un plan
Question 1 :
Soit ![]() un point de l’espace et
un point de l’espace et ![]() sont image par
sont image par ![]() . On sait que
. On sait que ![]() , donc ses coordonnées vérifient:
, donc ses coordonnées vérifient:
![]() . De plus,
. De plus, ![]() est orthogonal à
est orthogonal à ![]() (par définition de la projection orthogonale), donc
(par définition de la projection orthogonale), donc
![]() est colinéaire au vecteur normal de
est colinéaire au vecteur normal de ![]() ,
, 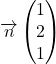 . Il existe donc un réel
. Il existe donc un réel ![]() tel que
tel que ![]() , ou encore:
, ou encore:
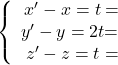
![]()
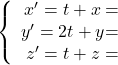
![]()
![]()
![]()
Finalement, une expression analytique de la projection orthogonale ![]() sur
sur ![]() est:
est:
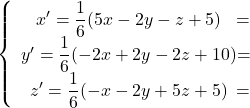
Question 2 :
Soit ![]() . Le point
. Le point ![]() étant le projeté orthogonal de
étant le projeté orthogonal de ![]() sur
sur ![]() , nous avons
, nous avons ![]() .
.
D’après le théorème de Pythagore, nous avons:
![]()
De plus, on constate que ![]() si et seulement si
si et seulement si ![]() , c’est-à-dire si, et seulement si
, c’est-à-dire si, et seulement si ![]() .
.
Retrouvez d’autres exercices et corrigés des cours de maths niveau terminale S2 :

