Mon parcours pour réussir en maths
J'aprends le cours par coeur
Je travaille avec un prof de maths
Je travaille entre chaque séance
Avis Google France
★★★★★ 4,8 sur 5
Exercices corrigés vecteurs en seconde
Résumé de cours Exercices et corrigés
Cours en ligne de Seconde Générale
Abordez les vecteurs sous un nouvel angle avec nos exercices spécialement élaborés pour les élèves de seconde. Ces activités vous guideront à travers des applications concrètes et variées, essentielles pour exceller en géométrie. Pour ceux qui cherchent à renforcer davantage leur compréhension, prendre des cours particuliers avec un cours de maths particulier peut apporter une aide adaptée et approfondie sur les vecteurs et sur les autres chapitres de seconde, accélérant ainsi l’apprentissage et la maîtrise de ces concepts essentiels.
Exercices 1 pour apprendre les vecteurs en maths seconde
Soient ![]() et
et ![]() quatre points du plan.
quatre points du plan.
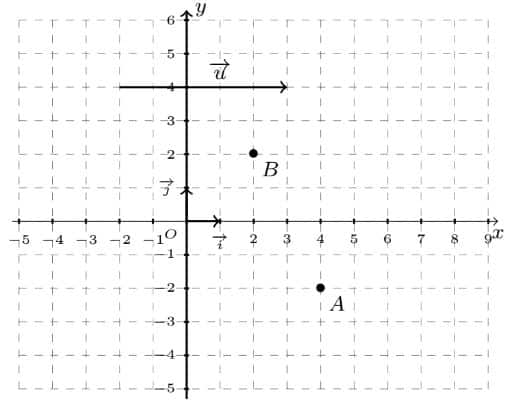
1. Par lecture graphique, donner le réel ![]() tel que
tel que ![]() .
.
2. Soit ![]() un point du plan tel que
un point du plan tel que ![]() .
.
Construire le vecteur ![]() , le vecteur
, le vecteur ![]() et le vecteur
et le vecteur ![]() .
.
3. Déterminer les vecteurs ![]() et
et ![]() en fonction de
en fonction de ![]() et
et ![]() .
.
4. Déterminer les réels ![]() et
et ![]() pour que
pour que ![]() .
.
Avis Google France ★★★★★ 4,8 sur 5COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Entrainement 2 de maths pour la seconde : Les vecteurs
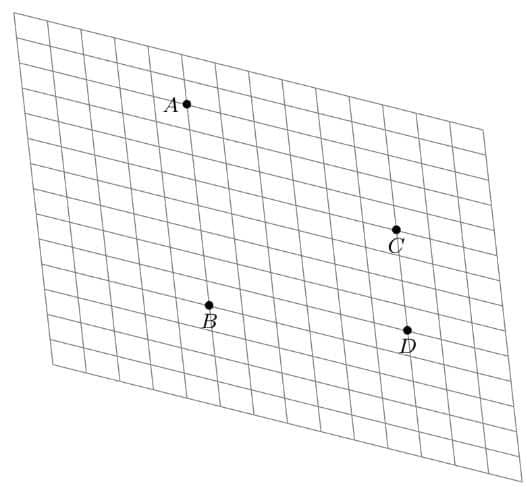
Un quadrilatère ![]() est un parallélogramme si et seulement si l’une des égalités suivantes est satisfaite :
est un parallélogramme si et seulement si l’une des égalités suivantes est satisfaite :
![]() Les côtés opposés ont la même mesure et sont parallèles
Les côtés opposés ont la même mesure et sont parallèles
![]() Les côtés opposés ont la même mesure et sont parallèles
Les côtés opposés ont la même mesure et sont parallèles
![]() La diagonale est égale à la somme des deux côtés
La diagonale est égale à la somme des deux côtés
![]() La diagonale est égale à la somme des deux côtés
La diagonale est égale à la somme des deux côtés
Soient ![]() un parallélogramme de centre
un parallélogramme de centre ![]() .
.
Montrer que ![]() .
.
Exercice 3 de seconde en maths à propos des vecteurs
Le plan est muni d’un repère orthonormé ![]() .
.
On considère le vecteur ![]() représenté sur la figure ci-après et deux points
représenté sur la figure ci-après et deux points ![]() et
et ![]() .
.
1. Construire le point ![]() , l’image du point
, l’image du point ![]() par la translation de vecteur
par la translation de vecteur ![]() ;
;
Puis le point ![]() , l’image du point
, l’image du point ![]() par la translation de vecteur
par la translation de vecteur ![]() .
.
2. Déterminer la nature du quadrilatère ![]() .
.
3. Par lecture graphique, donner les coordonnées des points ![]() et
et ![]() .
.
4. Calculer les coordonnées du point ![]() , le centre du quadrilatère
, le centre du quadrilatère ![]() .
.
5. Déterminer les coordonnées des vecteurs ![]() et
et ![]() .
.
Que peut-on en conclure ?
Quiz 4 de maths en seconde sur les vecteurs
Le plan est muni d’un repère orthonormé ![]() .
.
On considère ![]() ,
, ![]() et
et ![]() trois points du plan.
trois points du plan.
La fonction du script suivant ne demande aucun argument, mais demandera à l’utilisateur de saisir six nombres.

1. Compléter les pointillées à la ligne 11 et à la ligne 12.
2. Que reçoit-elle la variable det ?
3. Quelles sont les valeurs de renvoi de cette fonction?
4. Que renvoie cette fonction pour ![]() ,
, ![]() et
et ![]() .
.
Justifier votre réponse par des calculs.
STAGE INTENSIF SECONDE
Travailler les maths en seconde générale en stage de vacances
–> Stage de perfectionnement ou de remise à niveau
–> Préparer la spécialité maths dès la 2nde
–> Petits groupes en stage de maths en seconde
Avis Google France ★★★★★ 4,9 sur 5
Corrigé du test 1 sur les vecteurs de niveau seconde en maths
1. Par lecture graphique, on constate que ![]() .
.
Donc, pour que ![]() , on a
, on a ![]() .
.
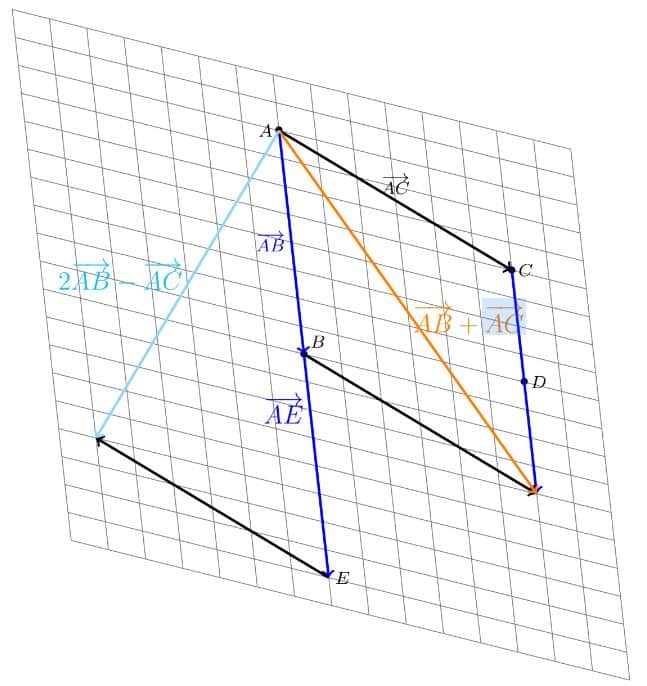
2. Le graphique est donné à la fin de l’exercice.
3. Par la relation de Chasles, ![]() :
:
D’après la question 1., ![]() .
.
Ce qui donne ![]() .
.
D’après la question 1., ![]() .
.
4. Soient les réels ![]() et
et ![]() . Par la relation de Chasles:
. Par la relation de Chasles: ![]() .
.
Comme ![]() ,
, ![]() et
et ![]() et
et
![]() ,
,
Alors ![]() .
.
Ce qui donne ![]() .
.
Par conséquent, ![]()
Avec ![]() et
et ![]() .
.
Réponse 2 sur les vecteurs pour réviser les maths en seconde
On a un parallélogramme ![]() de centre
de centre ![]() . On garde le vecteur
. On garde le vecteur ![]() , puis on utilisera la relation de Chasles pour décomposer les autres vecteurs, en passant par le point
, puis on utilisera la relation de Chasles pour décomposer les autres vecteurs, en passant par le point ![]() .
.
Alors :
![]()
![]()
![]()
![]()
![]()
Ainsi, ![]() .
.
Corrigé du test 3 de maths en seconde : Les vecteurs
On munit le plan d’un repère orthonormé ![]() . On donne le vecteur
. On donne le vecteur ![]() ainsi que deux points
ainsi que deux points ![]() et
et ![]() .
.
1. En plaçant les points ![]() et
et ![]() , on obtient la figure suivante :
, on obtient la figure suivante :
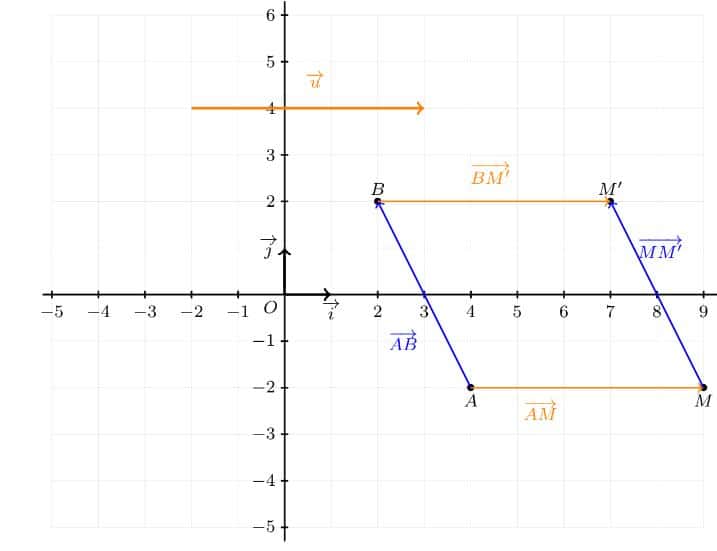
2. On considère le quadrilatère ![]() . Alors:
. Alors:
Sachant que 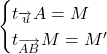 ,
,
On a 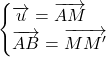
Par la relation de Chasles, ![]() ;
;
Par la relation de Chasles, ![]() ;
;
Sachant que ![]() ,
,
![]() .
.
Ce qui donne ![]() . Ce qui montre que le quadrilatère
. Ce qui montre que le quadrilatère ![]() est un parallélogramme.
est un parallélogramme.
3. Par lecture graphique :
Les coordonnées du point ![]() sont
sont ![]() ;
;
Les coordonnées du point ![]() sont
sont ![]() ;
;
Les coordonnées du point ![]() sont
sont ![]() ;
;
Les coordonnées du point ![]() sont
sont ![]() .
.
On a le point ![]() , le centre du parallélogramme
, le centre du parallélogramme ![]() .
.
Alors, ![]() est le milieu des diagonales
est le milieu des diagonales ![]() et
et ![]() .
.
Avec le segment ![]() ,
, ![]()
![]() .
.
Donc
![]()
![]() .
.
Ce qui conduit à 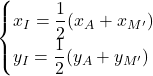
Donc, les coordonnées du point ![]() sont
sont ![]() .
.
En utilisant les coordonnées des points ![]() et
et ![]() :
:
Le vecteur ![]() a pour coordonnées
a pour coordonnées
![]() ;
;
Le vecteur ![]() a pour coordonnées
a pour coordonnées
![]() ;
;
Le vecteur ![]() a pour coordonnées
a pour coordonnées
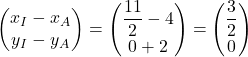 ;
;
Le vecteur ![]() a pour coordonnées
a pour coordonnées
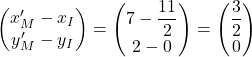 .
.
On conclut que ![]() et
et ![]() sont des vecteurs égaux. De même pour
sont des vecteurs égaux. De même pour ![]() et
et ![]() .
.
Correction à l’entrainement 4 de maths niveau seconde sur les vecteurs
On considère le repère ![]() et les points
et les points ![]() ,
, ![]() et
et ![]() du plan.
du plan.
1. On a le programme complété :

2. La variable det reçoit la valeur du déterminant des vecteurs ![]() et
et ![]() .
.
3. Cette fonction renvoie à une booléenne qui prend la valeur True ou False selon l’alignement des vecteurs ![]() et
et ![]() .
.
Avec les points ![]() ,
, ![]() et
et ![]() , cette fonction retourne True. Donc, les points
, cette fonction retourne True. Donc, les points ![]() et
et ![]() sont alignés.
sont alignés.
En effet, en posant ![]() , on a:
, on a:
![]()
![]()
![]()
Alors, la variable det reçoit la valeur ![]() .
.
Retrouvez d’autres exercices en ligne de maths seconde sur notre site :
- Quelques exercices sur les équations de droites en seconde
- Pourcentages : entrainement gratuit pour la seconde
- Révision des statistiques pour les maths en seconde
- Cours maths seconde sur les probabilités
- Test et correction de maths en seconde sur les ensembles et intervalles
- Cours complet de maths en seconde sur les équations de droites
- Fiche de cours de maths en seconde pour maitriser les pourcentages