Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Avis Google France
★★★★★ 4,8 sur 5

Cours sur les statistiques en seconde

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Seconde générale

Les cours sur les statistiques, font partie des cours importants de mathématique en seconde générale. Découvrez toutes les définitions indispensables pour réussir en maths en 2nde et préparer au mieux la classe de première en spécialité ! N’hésitez pas à envisager un professeur particulier maths peut être une excellente option si vous souhaitez approfondir vos acquis des notions mathématiques.

Cours statistiques en seconde : vocabulaire

Une étude statistique commence par un recueil de données. On utilise le vocabulaire suivant pour décrire cette étude :

Série statistique : Ensemble des valeurs collectées.

Population : Ensemble sur lequel porte l’étude statistique.

Individus : Éléments qui composent la population.

Échantillon : Partie de la population.

Caractère étudié : Propriété que l’on observe sur les individus. Les différentes valeurs obtenues sont appelées valeurs du caractère ou modalités, souvent notées $x_1$ , $x_2,\ldots x_p$ . On distingue deux types de caractères.

Un caractère peut être qualitatif (situation de famille, sexe, couleur des yeux, type d’habitation).

Un caractère peut être quantitatif. Il est dit discret lorsqu’il ne prend que des valeurs isolées (nombre d’enfants, notes dans une classe…).

Il est dit continu lorsqu’il peut prendre théoriquement toutes les valeurs d’un intervalle (taille, temps d’écoute…) ; dans ce cas, les valeurs sont regroupées en intervalles appelés des classes.

Effectif : Pour une valeur du caractère (modalité ou classe), on appelle effectif le nombre d’individus de la population ayant cette valeur.

On note souvent $n_1$ , $n_2,\ldots n_p$ les effectifs respectifs des modalités $x_1$ , $x_2,\ldots x_p$ .

Effectif total : Nombre total d’individus de la population (ou de l’échantillon). Il est égal à $n_1+n_2+\ldots +n_p$ , souvent noté $N$ .

Fréquence : Pour une valeur du caractère (modalité ou classe), on appelle fréquence le quotient de l’effectif de cette valeur par l’effectif total.

On note souvent $f_1$ , $f_2,\ldots,\ f_p$ les fréquences respectives des modalités $x_1$ , $x_2,\ldots x_p$ ,

Donc : $f_1=\dfrac{n_1}{N}$ , $f_2=\dfrac{n_2}{N}$ ,… $f_p=\dfrac{n_p}{N}$

On en déduit que $0\leq f_1\leq 1$ , $0\leq f_2\leq 1,\ldots,$ $0\leq f_p\leq 1$ , et $f_1+f_2+\ldots f_p=1$ .

Valeurs extrêmes : Valeurs minimales et maximales d’un caractère quantitatif.

Effectif cumulé : Pour une valeur $x$ d’une série statistique quantitative, l’effectif cumulé croissant (respectivement décroissant) de $x$ est la somme des effectifs des valeurs inférieures (respectivement supérieures) ou égales à $x$ .

Fréquence cumulée : Pour une valeur $x$ d’une série statistique quantitative, la fréquence cumulée croissante (respectivement décroissante) de $x$ est la somme des fréquences des valeurs inférieures (respectivement supérieures) ou égales à $x$ .

Exemple avec des notes :

Dans le tableau suivant sont regroupées les notes obtenues par les élèves d’une seconde lors du contrôle 1 (éventuellement arrondies pour simplifier l’étude) :

Dans cet exemple :

La série statistique est l’ensemble des notes collectées.

La population est l’ensemble des élèves de seconde.

Les individus sont chacun des élèves de seconde Turner.

Le caractère étudié est le résultat obtenu au contrôle 1.

Les modalités sont les valeurs chiffrées des notes obtenues au contrôle 1.

L’effectif total est le nombre d’élèves de la classe, à savoir 34.

Les valeurs extrêmes sont 4 et 19.

Exemple avec des notes :

Pour une meilleure lisibilité et pour simplifier l’étude, on peut commencer par compter le nombre d’individus ayant obtenu chaque note :

Remarque

Dans le tableau précédent, la somme des fréquences est supérieure à 1 à cause des arrondis.

Exemple : série continue
On a interrogé un échantillon de 4812 Français concernant la durée hebdomadaire d’écoute de la télévision (en heures) :

Le caractère étudié, à savoir la durée d’écoute, est quantitatif continu : il peut prendre théoriquement toutes les valeurs de l’intervalle $[0~;~50]$ .

Les données sont regroupées en classes $[0~;~10]$ ,

$[10~;~15[$ ,

$[15~;~20[$ ,

$[20~;~30[$ et $[30~;~50]$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Représentations graphiques : statistiques en maths 2nde

Séries à caractère quantitatif discret

Diagramme en bâtons

Dans un diagramme en bâtons, on représente une série statistique discrète par des segments dont la hauteur est proportionnelle à l’effectif de la valeur qu’ils représentent.

Exemple

On continue à travailler avec les données de l’exemple sur les notes. Voici le diagramme en bâtons de cette série :

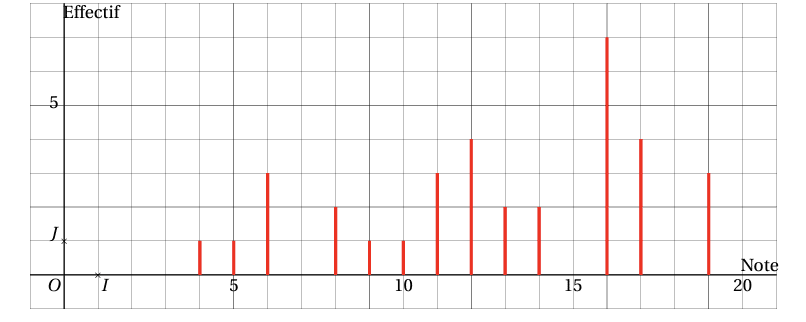
Diagramme circulaire

Exemple

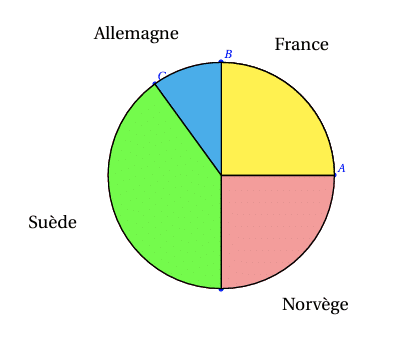
Dans une compétition d’athlétisme, quatre pays s’affontent : la France, l’Allemagne, la Suède et la Norvège.

On note le pourcentage de médailles obtenues par chacun des pays :

Représenter le diagramme circulaire associé à cette série statistique :

Pour cela, nous avons besoin des angles ; nous les calculons par proportionnalité, sachant que 100 % correspondent à 360 degrés.

Nuage de points

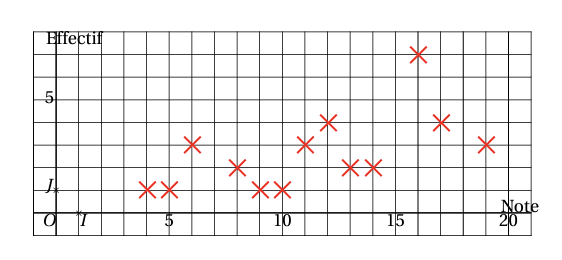
Dans un nuage de points, on représente une série statistique discrète par des points dont les abscisses sont les valeurs du caractère, et les ordonnées sont les effectifs correspondants, parfois reliés par des segments.

Exemple
On travaille toujours avec les données de l’exemple sur les notes. Voici le nuage de points de cette série :

Autre exemple, tiré du sujet de baccalauréat Polynésie :

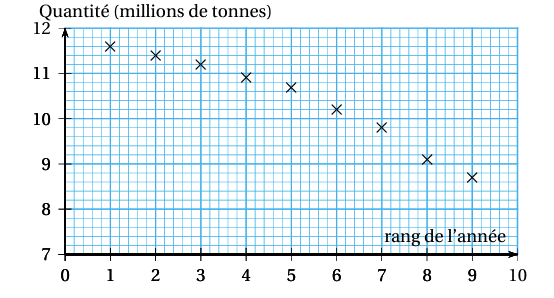
Le tableau ci-dessous donne les quantités de super sans plomb livrées et vendues en France (les quantités sont exprimées en millions de tonnes).

On représente alors les données sous forme de nuage de points en mettant en abscisses le rang de l’année et en ordonnées les quantités en (millions de tonnes)

Séries à caractère quantitatif continu : Histogramme

Dans un histogramme, on représente une série statistique continue par des rectangles dont la largeur correspond à l’amplitude de chaque classe et dont l’aire est proportionnelle à l’effectif de la classe.

Exemple

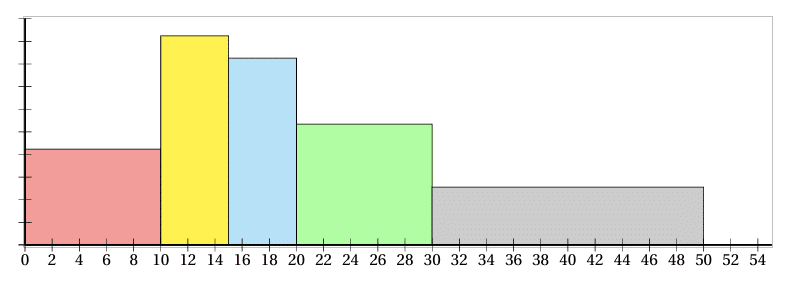
On travaille avec les données de l’exemple sur la durée d’écoute de la télévision.

Voici l’histogramme de cette série :

Remarque

Lorsque les classes ont toutes la même amplitude, la hauteur de chaque rectangle est proportionnelle à l’effectif de la classe qu’il représente. On dit alors que l’histogramme est à pas constant.

Polygone d’effectifs ou de fréquences cumulés

Le polygone des effectifs cumulés croissants (respectivement décroissants) d’une série statistique continue est la ligne brisée qui joint les points du plan dont les abscisses sont les bornes de chaque classe et dont les ordonnées sont les effectifs cumulés croissants (respectivement décroissants) de ces valeurs.

Le polygone des fréquences cumulées croissantes (respectivement décroissantes) d’une série statistique continue est la ligne brisée qui joint les points du plan dont les abscisses sont les bornes de chaque classe et dont les ordonnées sont les fréquences cumulées croissantes (respectivement décroissantes) de ces valeurs.

Ces représentations donnent l’allure de la répartition des valeurs de la série.

Exemple

La situation est toujours celle de l’exemple série continue. Le tableau des effectifs cumulés croissants est le suivant :

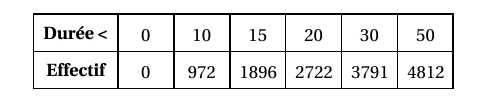
D’où le polygone des effectifs cumulés croissants

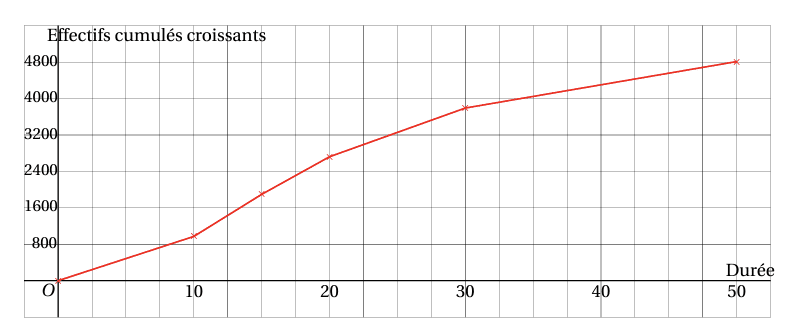
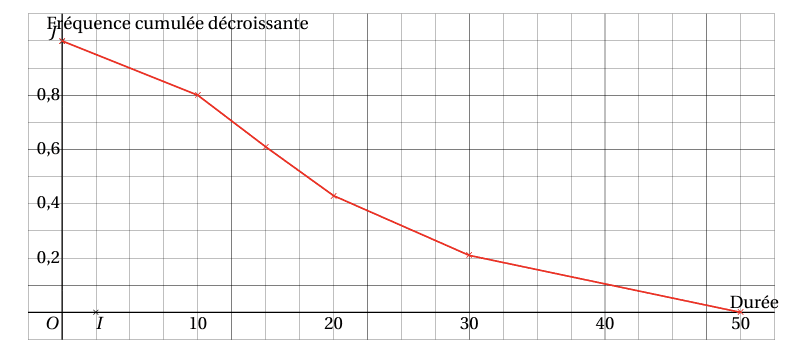
Traitons à présent le cas des fréquences cumulées décroissantes :

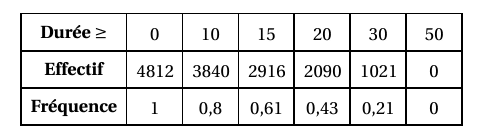
D’où le polygone des fréquences cumulées décroissantes :

Paramètres statistiques : résumé de cours en seconde maths

Paramètres de position

Définition

Un mode d’une série statistique est une valeur de la série dont l’effectif est strictement supérieur à celui des autres valeurs.

Remarque

Dans une série statistique, il peut y avoir plusieurs modes.

Exemple

Dans l’exemple sur les notes, le mode est 16.

Moyenne

On considère une série statistique donnée par le tableau suivant :

Définition

La moyenne de cette série statistique est le réel noté $\overline{x}$ défini par

$\overline{x}=\dfrac{n_1x_1+n_2x_2+\ldots+n_px_p}{n_1+n_2+\ldots n_p}$

= $\dfrac{n_1x_1+n_2x_2+\ldots+n_px_p}{N}$

En notant $N=n_1+n_2+\ldots+n_p$ l’effectif total de la série.

Propriété

On peut également calculer la moyenne à l’aide des fréquences :

$\overline{x}$ = $x1f_1+x_2f_2+\ldots+x_pf_p.$

Exemple

Avec les données de l’exemple ??, la moyenne de la classe est :

$\overline{x}=\dfrac{1\times 4+1\times 5+3\times 6+2\times 8+1\times 9+1\times 10+3\times 11+4\times 12+2\times 13+2\times 14+7\times 16+4\times 17+3\times 19}{34}$

$=\dfrac{434}{34}$

Une valeur approchée de $\overline{x}$ à $10^{-2}$ près est 12,76.

STAGE INTENSIF SECONDE

Travailler les maths en seconde générale en stage de vacances

–> Stage de perfectionnement ou de remise à niveau
–> Préparer la spécialité maths dès la 2nde
–> Petits groupes en stage de maths en seconde

Avis Google France ★★★★★ 4,9 sur 5

Médiane

Définition

La médiane $M$ d’une série statistique est un réel qui partage cette série en deux parties telles que :

Au moins 50 % des valeurs sont inférieures ou égales à la médiane ;

Au moins 50 % des valeurs sont supérieures ou égales à la médiane.

Propriété

En pratique, on adopte la démarche suivante pour déterminer la médiane $M$ d’une série statistiques d’effectif total $N$ :

On range d’abord les $N$ valeurs du caractère par ordre croissant.

Si $N$ est pair, $N=2p$ , $M$ est la moyenne des deux valeurs $\og$ centrales $\fg$ de la série,

C’est-à-dire $M=\dfrac{x_N+x_{N+1}}{2}$ .

Si $N$ est impair, $N=2p+1$ , $M$ est la valeur centrale de la série, c’est-à-dire $x_{p+1}$ .

Exemple

Dans l’exemple exemple notes, l’effectif total est 34, c’est-à -dire pair. $34=2\times 17$ .

La médiane est donc la moyenne des deux valeurs centrales de la série, à savoir les 17ème et 18ème valeurs.

Donc $M=\dfrac{13+13}{2}=13$ ,

Ce qui signifie qu’au moins la moitié des notes est inférieure ou égale à 12, et qu’au moins la moitié des notes est supérieure ou égale à 12.

Exemple

En France, dans le secteur privé et semi-public (SNCF, Poste, Caisse d’épargne…), le salaire net mensuel médian est de 1528 €, (ce qui signifie que la moitié des salariés de ces entreprises touchent moins que cette valeur) alors que le salaire net mensuel moyen est de 1903,5 €. (somme de tous les salaires divisée par le nombre de salariés).

Paramètres de dispersion : Étendue

Définition

L’étendue d’une série statistique est la différence entre sa plus grande et sa plus petite valeur.

Exemple

Dans l’exemple sur les notes, l’étendue est égale à $19-4=15$ .

Quartiles

Définition

On considère une série statistique.

Le premier quartile $Q_1$ est la plus petite valeur de la série telle qu’au moins 25 % des données soient inférieures ou égales à $Q_1$ .

Le troisième quartile $Q_3$ est la plus petite valeur de la série telle qu’au moins 75 % des données soient inférieures ou égales à $Q_3$ .

Exemple

On considère toujours les données de l’exemple « exemple notes ».

$34\times \dfrac{25}{100} = 8,5$ donc le premier quartile $Q_1$ de la série est la 9ème valeur,

D’où $Q_1 = 10$ , ce qui signifie qu’au moins un quart des notes sont inférieures ou égales à 10 (en réalité 9 notes, soit environ 26 %).

$34\times\dfrac{75}{100} = 25,5$ donc le troisième quartile $Q_3$ de la série est la 26ème valeur,

D’où $Q_3 = 16$ , ce qui signifie qu’au moins trois quarts des notes sont inférieures ou égales à 16 (en réalité 27 notes, soit environ 79 %).

Remarque

Le fait que le partage théorique en 25 %, 50 % et 75 % de la série statistique à l’aide des indicateurs

$Q_1$ , $M$ et $Q_3$ ne soit pas tout à fait exact provient du fait que la série comporte des valeurs identiques.

Ce phénomène a tendance à s’amoindrir lors d’une étude sur une population plus importante avec un caractère dont les modalités sont plus disparates.

Écart interquartile

Définition

On considère une série statistique de premier quartile $Q_1$ et de troisième quartile $Q_3$ .

On appelle intervalle interquartile l’intervalle $[Q_1~;~Q_3]$ .

On appelle écart interquartile la différence $Q_3-Q_1$ .

Exemple

Dans l’exemple « exemple notes », l’intervalle interquartile est $[10~;~16]$ et l’écart interquartile est $Q_3-Q_1 = 16-10 = 6$ .

Retrouvez d’autres cours en ligne de maths seconde sur notre site :

Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Cours sur les statistiques en seconde

Cours statistiques en seconde : vocabulaire

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Représentations graphiques : statistiques en maths 2nde

Séries à caractère quantitatif discret

Diagramme circulaire

Nuage de points

Séries à caractère quantitatif continu : Histogramme

Paramètres statistiques : résumé de cours en seconde maths

Paramètres de position

Moyenne

STAGE INTENSIF SECONDE

Médiane

Paramètres de dispersion : Étendue

Quartiles

Écart interquartile

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales