Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Nombres complexes en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Résumé de cours et méthodes – sommes trigonométriques, linéarisation
Méthode 1 : Passer de la forme algébrique à la forme exponentielle et réciproquement.
Pour passer de la forme algébrique ![]() (supposé non nul avec
(supposé non nul avec ![]() ) à la forme exponentielle (
) à la forme exponentielle (![]() ), il faut commencer par factoriser par le module du nombre complexe et essayer de reconnaître un argument. On commencera donc par calculer
), il faut commencer par factoriser par le module du nombre complexe et essayer de reconnaître un argument. On commencera donc par calculer ![]() et on trouvera un réel
et on trouvera un réel ![]() tel que :
tel que :
![]()
Le passage de la forme exponentielle à la forme algébrique est plus simple, il suffit de calculer l’exponentielle.
Exemple : Soit ![]()
Mettre sous forme exponentielle le nombre complexe suivant : ![]() .
.
Réponse :
En factorisant par ![]() on a
on a
![]()
Ici, on pourrait penser que l’on a fini, il faut quand même vérifier que
Comme ![]() on a bien
on a bien ![]()
Méthode 2 : Utiliser l’écriture exponentielle d’un nombre complexe.
On utilisera cette méthode pour calculer les puissances d’un nombre complexe.
Exemple : Calculer ![]()
Réponse : On pourrait utiliser la formule du binôme de Newton mais après on serait bloqué…
On écrit ![]() sous forme exponentielle, ainsi
sous forme exponentielle, ainsi ![]() puis
puis ![]() . Comme
. Comme ![]() on a
on a
![]()
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Méthode 3 : Calculer des sommes trigonométriques.
Si l’on doit calculer des sommes faisant apparaître des ![]() et/ou des
et/ou des ![]() il faut penser à utiliser les formules d’Euler :
il faut penser à utiliser les formules d’Euler :![]() et
et ![]()
Ou bien de manière équivalente, on a :
![]()
Exemple : Soient ![]() et
et ![]() ,
,
Réponse :
Pour cela, écrivons![]()
= 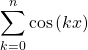
= 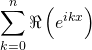
= 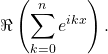
Cette dernière somme est la somme des termes d’une suite géométrique de raison ![]() , ainsi
, ainsi![]()
= 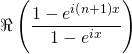
=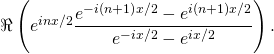
En appliquant les formules d’Euler, on a finalement :
![]()
= 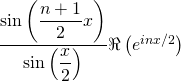
= 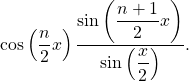
N’hésitez pas à suivre des cours de maths particuliers pour vous perfectionner en maths en ECG1.
Méthode 4 : Linéariser des ![]() et
et ![]() .
.
On utilise les formules d’Euler rappelées ci-dessus pour pouvoir obtenir une expression linéarisée (c’est-à-dire qu’il n’y a plus de puissances mais seulement des termes de la forme ![]() et/ou
et/ou ![]() ) de
) de ![]() et/ou
et/ou ![]() .
.
Il faudra se souvenir de cette méthode, notamment pour le calcul de primitives d’expressions polynomiales en ![]() et/ou
et/ou ![]()
Exemple : Que vaut ![]() après linéarisation ?
après linéarisation ?
Réponse : On utilise la formule d’Euler puis le binôme de Newton et on écrit
![]()
=![]()
=![]()
=![]()
Méthode 5 : Utiliser les racines ![]() -ièmes de l’unité.
-ièmes de l’unité.
Dans ![]() l’équation
l’équation ![]() admet exactement
admet exactement ![]() solutions : les racines
solutions : les racines ![]() -ièmes de l’unité
-ièmes de l’unité
![]()
Intéressons-nous à la résolution dans ![]() de l’équation
de l’équation ![]() avec
avec ![]() et
et ![]()
Si l’on écrit ![]() (forme exponentielle), alors il suffit de trouver une solution particulière de l’équation
(forme exponentielle), alors il suffit de trouver une solution particulière de l’équation ![]() Par exemple,
Par exemple, ![]() convient.
convient.
Exemple : Quel est l’ensemble des solutions de l’équation :
![]()
Réponse :
![Rendered by QuickLaTeX.com \left\{^{1 / 7} e^{i \dfrac{\pi}{2 21}} \times e^{2i k \pi / 7 }, \, k \in [\![ 0 , 6 ]\!] \right\}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-df8dc314713372943bb005466f334a1f_l3.png)
Méthode 6 : Calculer les racines carrées d’un nombre complexe en l’absence d’une forme exponentielle simple.
Rappelons que la notation ![]() n’a pas de sens ! D’ailleurs, un nombre complexe non nul admet deux racines carrées (c’est-à-dire qu’il existe deux nombres
n’a pas de sens ! D’ailleurs, un nombre complexe non nul admet deux racines carrées (c’est-à-dire qu’il existe deux nombres ![]() tels que
tels que ![]() ).
).
Exemple :
Quelles sont les racines carrées de ![]() ?
?
(i) ![]()
![]()
(ii) ![]()
![]()
(iii) ![]()
![]()
Réponse :
Soit ![]() tel que
tel que ![]() =
= ![]() =
=![]()
Cela nous donne ![]() =
= ![]()
En calculant le module, on obtient ![]() soit
soit ![]() Nous avons ainsi les relations suivantes :
Nous avons ainsi les relations suivantes :
![Rendered by QuickLaTeX.com \[\begin{cases} a^2 - b^2 & = 3 \\ a^2 + b^2 & =\sqrt{13} \\ 2ab & = 2 \\ \end{cases}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a3b36a294699e533b43bccf9790223f2_l3.png)
En sommant les deux premières lignes, on a ![]()
![]() Si
Si ![]() alors la troisième équation donne
alors la troisième équation donne ![]()
![]() Si
Si ![]() alors la troisième équation donne
alors la troisième équation donne ![]()
Les deux racines carrées de ![]() sont, après avoir utilisé l’expression conjuguée,
sont, après avoir utilisé l’expression conjuguée, ![]() et
et ![]()
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
Les mathématiques sont une matière difficile, pour réussir en ECG1 il est fondamental de bien connaître l’ensemble de ces cours de maths. Servez-vous des nombreux autres cours en ligne pour garder un bon niveau :

