Cours en ligne Physique en Maths Sup

Chapitres Physique en MPSI, PCSI, MP2I, PTSI

Cours de Physique : Superposition en Maths Sup

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de physique en Maths Sup

Ce cours gratuit de physique chimie en CPGE vous assistera pour revoir le cours de la superposition en maths sup. N’hésitez pas à prendre un prof particulier en physique chimie pour bénéficier d’une attention individualisée et d’un soutien adapté à vos besoins spécifiques. Vous aurez la liberté, l’efficacité et un soutien scolaire innovant pour maîtriser pleinement les concepts de superposition en MPSI, PCSI, PTSI.

Résumé de cours et méthodes – maths sup superposition

Plan :

A. Interférences
B. Battements (PCSI)
C. Ondes stationnaires
D. Diffraction
E. Polarisation (PCSI)

Tu veux réussir en physique chimie ?

Accède aux meilleurs exercices et résumés de cours

Travaille sur les annales en autonomie

Fais toi accompagner en cours à domicile

Les élèves que nous aidons en cours de physique -chimie à domicile recommandent à 98% nos profs

Avis Google France
★★★★★ 4,9 sur 5

A. Interférences

1. Principe d’interférences, division d’ondes.
Il ne peut y avoir de phénomène d’interférences qu’entre deux ondes de même pulsation. C’est pourquoi il faut disposer expérimentalement d’un diviseur d’onde :
* diviseur d’amplitude où en un point de l’espace l’onde se divise en deux fractions
* diviseur de front d’onde où deux pupilles prélèvent en deux lieux distants deux fractions d’une même onde étendue.

Exemple.
En optique, il existe deux familles de diviseur d’onde :
* le miroir semi-réfléchissant
* les dispositifs organisant une déviation distincte selon l’endroit où la lumière arrive.
À quelle famille appartiennent-ils ?

Correction :

La division de l’onde se fait en un même point dans le cas du miroir semi-réfléchissant (un photon sur deu est réfléchi, un sur deux traverse).
C’est donc un diviseur d’amplitude.
Dans le second cas, on prélève une fraction de l’onde en deux endroits différents, c’est un diviseur de front d’onde.

2. Principe de superposition.
En un point $M$ de l’espace où arrivent deux ondes issues de la division d’une même onde, le signal résultant est le somme des deux signaux :
c’est le principe de superposition et sa traduction mathématique est
$s(M,t)=s_1(M,t)+s_2(M,t)$

Exemple.
$s_1(M,t)=A\cos(\omega t+\varphi)$
et $s_2(M,t)=A\cos(\omega t-\varphi)$
Quelle est l’onde résultante ?

Correction :

$s(M,t)=2A\cos\varphi\cos(\omega t)$
Son amplitude $2A\cos\varphi$ est donc inférieure à la somme $2A$ des amplitudes des deux ondes.

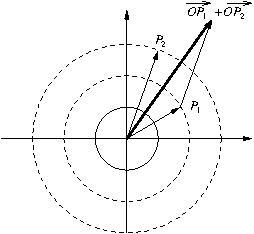
3. Construction de Fresnel.
L’onde résultant de l’interférence de deux ondes de même pulsation et de même phase à l’origine, donc résultant de la division d’une même onde sinusoïdale (ou monochromatique) peut s’écrire sous la forme
$s(M,t)=A_1\cos(\omega t+\varphi_1)+$

$A_2\cos(\omega t+\varphi_2)$
$\varphi_1\neq\varphi_2$ en général car le délai de propagation de l’onde de la source à $M$ pour la fraction (1) de l’onde est différent de celui pour la fraction (2). Leurs phases sont distinctes, on dit qu’elles sont déphasées.
On peut exprimer

$s(M,t)=A\cos(\omega t+\varphi)$
en utilisant les formules de trigonométrie, mais il est plus rapide d’utiliser une construction graphique :
la construction de Fresnel.

On construit ainsi deux vecteurs dans le plan $(O,x,y)$ , $\vec{OP_1}$ de coordonnées polaires
$(r=A_1,\theta=\varphi_1)$

et $\vec{OP_2}$ de coordonnées polaires
$(r=A_2,\theta=\varphi_2)$ .

Le vecteur $\vec{OP_1}+\vec{OP_2}$
a pour coordonnées polaires $r=A$ et $\theta=\varphi$ .

Exemple.
Quelle est l’amplitude et la phase de la superposition de
$2\cos(\omega t+\pi/6)$ et $3\cos(\omega t+\pi/3)$ ?

Correction :

On lit sur le schéma $A\simeq 4,7$ et $\varphi\simeq 50^{\circ}$

4. Interférences constructives, destructives.
Deux cas particuliers sont à mentionner.
* Si $\varphi=\varphi_2=n\cdot 2\pi$ avec $n$ entier

alors les deux vecteurs de Fresnel sont colinéaires et $A=A_1+A_2$
On dit qu’il y a interférences constructives.
* Si $\varphi=\varphi_2=\pi+n\cdot 2\pi$ avec $n$ entier

alors les deux vecteurs de Fresnel sont anticolinéaires et $A=|A_1-A_2|$
On dit qu’il y a interférences destructives.

Exemple.
Quel type d’interférences observe-t-on entre
$s_1(M,t)=A\cos(\omega t+2\pi/3)$
et $s_2(M,t)=A\sin(\omega t+\pi/6)$ ?

Correction :

La propriété de trigonométrie
$\cos(\alpha-\pi/2)=\sin\alpha$
permet d’écrire
$s_2(M,t)=A\cos(\omega t+\pi/6-\pi/2)$
$s_2(M,t)=A\cos(\omega t-\pi/3)=-s_1(t)$
On en déduit $s(M,t)=0$
il y a interférences destructives.

COURS DE PHYSIQUE-CHIMIE

Nous avons sélectionné pour vous les meilleurs profs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES

Avis Google France ★★★★★ 4,9 sur 5

B. Battements (PCSI)

1. Description algébrique des battements.
Le phénomène de battements intervient lorsqu’on superpose deux signaux de même amplitude, mais de fréquences très proches
$f_1=f_0(1-\varepsilon)$
et $f_2=f_0(1+\varepsilon)$
avec $\varepsilon\ll 1$
On observe alors un signal de fréquence $f_0$ modulé par une enveloppe dont l’amplitude varie avec une très petite fréquence (donc une très grande période).

Démonstration de cours.
Montrer le résultat énoncé en utilisant les formules de trigonométrie.

Correction :

On a
$s_1(t)=C\cos(2\pi f_0t-2\pi\varepsilon f_0t)$
$s_2(t)=C\cos(2\pi f_0t+2\pi\varepsilon f_0t)$
Or $\cos(p-q)=\cos p\cos q+\sin p\sin q$
$\cos(p+q)=\cos p\cos q-\sin p\sin q$
donc
$s(t)=s_1(t)+s_2(t)$
$=2C\cos(2\pi f_0t)\cos(2\pi\varepsilon f_0t)$
On peut donc l’assimiler à une fonction sinusoïdale de fréquence $f_0$ dont l’amplitude varie au cours du temps entre $0$ et $2C$

2. Description graphique des battements.
La fonction mathématique qui décrit les battements est le produit
* d’une fonction « nerveuse » (de grande fréquence) appelée la porteuse
$s_P(t)=\cos(2\pi f_0t)$
de période $T_p=1/f_0$
* et d’une fonction qui module l’amplitude appelée l’enveloppe
$s_e(t)=2C\cos(2\pi\varepsilon f_0t)$
de période
$T_e=1/(\varepsilon f_0)=T_p/\varepsilon \gg T_p$

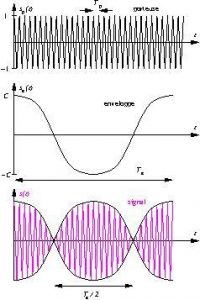
Réciproquement, à partir du graphe du signal, il est possible de retrouver les deux fréquences proches.
On mesure les périodes de la porteuse et de l’enveloppe et on en déduit les valeurs de $f_0$ et de $\varepsilon$

Exemple.
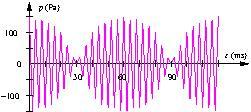
Voici le graphe d’un signal faisant apparaître un battement. Déterminer les fréquences de deux signaux superposés.

Correction :

La période de l’enveloppe vaut $T_p=120~\mathrm{ms}$ (attention au piège !).
Pendant cette période, on dénombre 32 vibrations de la porteuse donc
$\varepsilon=1/32$
$T_e=3,75~\mathrm{ms}$
et $f_0=1/T_e=267~\mathrm{Hz}$

C. Ondes stationnaires

1. Superposition de deux ondes $\pm k$
La superposition sur un axe $(O,x)$ de deux ondes de même pulsation, de même amplitude et de sens de propagation opposés donne une onde stationnaire :
$C\cos(\omega t-kx)+C\cos(\omega t+kx)=$
$2C\cos(\omega t)\cos(kx)$
Il faut bien distinguer cette forme mathématique de la forme décrivant une onde progressive.

Celle-ci est le produit d’une fonction de $x$ seulement (terme spatial) par une fonction de $t$ seulement (terme temporel).

L’onde stationnaire a-t-elle la propriété de double périodicité, temporelle et spatial ?

$T=\frac{2\pi}{\omega}$
$\lambda=\frac{2\pi}{k}$
et $\lambda=cT$

2. Corde fixée à ses deux extrémités.
C’est un cas important où la solution du type onde stationnaire est adaptée. Une corde définie par $x\in[0,L]$ est le siège d’une onde transversale de vibration $y(x,t)$ qui se propage à la célérité $c$
Elle est fixe à ses deux extrémités donc
$\forall t,~y(0,t)=y(L,t)=0$
On cherche une solution stationnaire
$y(x,t)=C\cos(\omega t+\varphi)\cdot\cos(kx+\psi)$
Elle est fixe à ses deux extrémités donc
$\forall t,~y(0,t)=y(L,t)=0$ soit
$\forall t,~C\cos(\omega t+\varphi)\cdot \cos\psi=0$
$\forall t,~C\cos(\omega t+\varphi)\cdot \cos(kL+\psi)=0$
$\cos\psi=0$ et $\psi$ étant une phase, il est inutile de la donner avec un « modulo »
On choisit $\psi=-\pi/2$ par exemple
On a donc $\cos(kL-\pi/2)=0$
soit $\sin(kL)=0$ donc il y a quantification (apparition d’un nombre entier) $kL=n\pi$ avec $n$ entier naturel non nul. On en déduit la quantification des autres paramètres
$k=n\pi/L$
$L=n\lambda/2$
$\omega=n\pi c/L$
$f=\pi c/(2L)$
On a donc
$y(x,t)=C\cos(\omega t+\varphi)\sin(n\pi x/L)$
Il y a donc des noeuds de vibration pour $x=L/n$ et une forme de corde en $n$ fuseaux.

$x\in[0,L]$ est le siège d’une onde transversale de vibration $y(x,t)$ qui se propage à la célérité $c$ Elle est fixe à ses deux extrémités donc $\forall t,~y(0,t)=y(L,t)=0$ On cherche une solution stationnaire $y(x,t)=C\cos(\omega t+\varphi)\cdot\cos(kx+\psi)$ Elle est fixe à ses deux extrémités donc $\forall t,~y(0,t)=y(L,t)=0$ soit $\forall t,~C\cos(\omega t+\varphi)\cdot \cos\psi=0$ $\forall t,~C\cos(\omega t+\varphi)\cdot \cos(kL+\psi)=0$ $\cos\psi=0$ et $\psi$ étant une phase, il est inutile de la donner avec un ``modulo » On choisit $\psi=-\pi/2$ par exemple On a donc $\cos(kL-\pi/2)=0$ soit $\sin(kL)=0$ donc il y a quantification (apparition d’un nombre entier) $kL=n\pi$ avec $n$ entier naturel non nul. On en déduit la quantification des autres paramètres $k=n\pi/L$ $L=n\lambda/2$ $\omega=n\pi c/L$ $f=\pi c/(2L)$ On a donc $y(x,t)=C\cos(\omega t+\varphi)\sin(n\pi x/L)$ Il y a donc des noeuds de vibration pour $x=L/n$ et une forme de corde en $n$ fuseaux. » width= »309″ height= »270″ />

3. Corde de Melde.
C’est une forme proche du cas précédent, mais cette fois, l’extrémité est fixe $y(L,t)=0$ et on impose une vibration par un excitateur $y(0,t)=C_0\cos(\omega t)$
On en déduit
$\forall t,~C\cos(\omega t+\varphi)\cdot \cos\psi=C_0\cos(\omega t)$
$\forall t,~C\cos(\omega t+\varphi)\cdot \cos(kL+\psi)=0$
donc $kL+\psi=\pi/2$ par exemple

donc $\forall t,$

$C\cos(\omega t+\varphi)\cdot \sin(kL)=C_0\cos(\omega t)$
donc $\varphi=0$ par exemple et
$\displaystyle{C=\frac{C_0}{\sin(kL)}}$

Démonstration de cours.

Montrer qu’il y a résonance si la pulsation de l’excitateur est égal à l’une des pulsations propres de la corde fixée à ses deux extrémités.

Correction :

Il y a résonance quand l’amplitude $C$ tend vers l’infini donc quand $\sin(kL)=0$ soit $k=n\frac{\pi}{L}$ avec $n$ entier soit $\omega=n\pi c/L$ qui correspond bien aux pulsations du cas précédent.

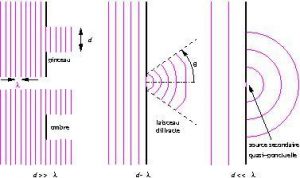
D. Diffraction

Le phénomène de diffraction intervient lorsqu’une onde plane incidente, de longueur d’onde $\lambda$ rencontre une paroi transpercée d’une fente ou d’un trou de largeur $d$ .
* Si $d\gg \lambda$ , l’onde est simplement réduite à une onde de largeur $d$
* Si $d$ est supérieur ou de l’ordre de $\lambda$ , l’onde est diffractée selon un dièdre ou un cône d’angle $\theta$ défini par
$\sin\theta\simeq\frac{\lambda}{d}$
* Si $d$ est inférieur ou très inférieur à $\lambda$ , la pupille se comporte comme une source ponctuelle et l’onde est diffractée dans toutes le directions dans le demi-espace en aval de la pupille.

$diffraction physique maths sup$

Exemple.
Lorsqu’un individu parle ou chante, pourquoi l’entend-on même si on n’est pas en face de lui ?

On donne :
* largeur de la bouche $d\simeq 5~\mathrm{cm}$
* célérité du son dans l’air $c=340~\mathrm{m\cdot s^{-1}}$
* fréquence typique de la voix $f=300~\mathrm{Hz}$

Correction :

On calcule $\lambda=c/f\simeq 1~\mathrm{m}$ donc $\lambda/d=20$ et la diffraction se fait bien dans toutes les directions.

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

E. Polarisation (PCSI)

1. Onde polarisée et polariseur.
Une onde électromagnétique plane et monochromatique (une seule couleur, une seule longueur d’one ou pulsation associée) est représentée par un champ électrique transversal.
Si l’onde se propage dans la direction et le sens de l’axe $(O,x)$ alors le champ électrique est orthogonal à cet axe et possède deux composantes selon $\vec{u}_y$ et $\vec{u}_z$
$\displaystyle{\vec{E}(M,t)=\left|\begin{array}{l}0 \\ E_y(x,t) \\ E_z(x,t)\end{array}\right.}$
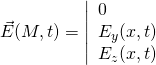
C’est donc la superposition de deux ondes progressives
$\vec{E}=E_y(x,t)\vec{u}_y+E_z(x,t)\vec{u}_z$
avec $E_y(x,t)=A\cos(\omega t-kx+\varphi_y)$
et $E_z(x,t)=B\cos(\omega t-kx+\varphi_z)$
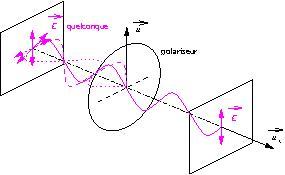
Il est possible de sélectionner une de ces deux ondes en utilisant une lame polarisante, ou polariseur.
Cette lame possède un axe privilégié, appelé axe transparent (par exemple $\vec{u}_y$ ) tel que si on la place orthogonalement à la direction de propagation de l’onde
(ici $\vec{u}_x$ ) la lame laisse passer la composante parallèle à son axe transparent (ici $\vec{u}_y$ ), et bloque la composante perpendiculaire (ici $\vec{u}_z$ )
Le champ de l’onde qui traverse cette lame vaudra donc
$\vec{E}'=E_y(x,t)\vec{u}_y+0\vec{u}_z$
Une telle onde est dite polarisée rectilignement.

Exemple.

Que se passe-t-il si on place un polariseur d’axe transparent $\vec{u}_z$ face à une onde polarisée selon $\vec{u}_y$ et se propageant dans la direction et le sens de $\vec{u}_x$ ?

Correction :

Il y a extinction complète car l’onde est polarisée selon l’axe opaque, et sa composante sur l’axe transparent est nulle.

2. Loi de Malus.
Lorsqu’une onde polarisée rectilignement dans la direction $\vec{u}$ et d’intensité lumineuse $\mathcal{I}$ traverse un polariseur d’axe transparent $\vec{u}_y$ , l’intensité de la lumière émergeante est
$\mathcal{I}'=\mathcal{I}\cos^2\alpha$
avec $\alpha=(\vec{u}_x,\vec{u})$

Exemple.
Quel est le rapport $\mathcal{I}'/\mathcal{I}$ si $\alpha =\pi/4$ ?

Correction :

Par application de la loi de Malus, ce rapport vaut
$\mathcal{I}'/\mathcal{I}=\cos^2\frac{\pi}{4}=\frac12$

Si vous sentez que vous avez quelques difficultés en physique en Maths Sup, ne tardez pas à travailler dessus. Effacez vos difficultés le plus tôt possible vous permettra de pouvoir suivre vos 2 années de prépa sereinement. Pour cela, n’hésitez pas à consulter ces quelques chapitres disponibles totalement gratuitement :

Cours de Physique : Superposition en Maths Sup

Résumé de cours et méthodes – maths sup superposition

Plan :

Tu veux réussir en physique chimie ?

Accède aux meilleurs exercices et résumés de cours

Travaille sur les annales en autonomie

Fais toi accompagner en cours à domicile

A. Interférences

COURS DE PHYSIQUE-CHIMIE

Nous avons sélectionné pour vous les meilleurs profs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES

B. Battements (PCSI)

C. Ondes stationnaires

D. Diffraction

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

E. Polarisation (PCSI)

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales