Chapitres Maths en ECS2
Cours : Algèbre bilinéaire en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Formes bilinéaires, Produit scalaire, Orthogonalité & Espace euclidien
1. Formes bilinéaires
Méthode 1 : Qu’est-ce qu’une forme bilinéaire sur ![]() ?
?
C’est une application ![]() qui à un couple
qui à un couple ![]() d’éléments de
d’éléments de ![]() associe un réel,
associe un réel, ![]() , qui vérifie les deux propriétés suivantes:
, qui vérifie les deux propriétés suivantes:
(i) pour ![]() fixé dans
fixé dans ![]() , l’application
, l’application ![]() définie par:
définie par: ![]() ,
, ![]() , est linéaire;
, est linéaire;
(ii) pour ![]() fixé dans
fixé dans ![]() , l’application
, l’application ![]() définie par:
définie par: ![]() ,
, ![]() , est linéaire.
, est linéaire.
La propriété (i) peut s’énoncer sous la forme: ![]() est linéaire par rapport à la deuxième variable, ou encore
est linéaire par rapport à la deuxième variable, ou encore ![]() est linéaire à droite, et la propriété (ii) sous la forme:
est linéaire à droite, et la propriété (ii) sous la forme: ![]() est linéaire par rapport à la première variable, ou
est linéaire par rapport à la première variable, ou ![]() est linéaire à gauche.
est linéaire à gauche.
N’hésitez pas à solliciter l’aide d’un professeur particulier de maths si vous éprouvez le moindre blocaquage en s’entrainant.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Exemple : ![]() est-elle une forme bilinéaire sur
est-elle une forme bilinéaire sur ![]() si pour tout
si pour tout ![]() :
:
(i) ![]() ?
?
(ii) ![]() ?
?
(iii) ![]() ?
?
Réponse :
(i) Non
(ii) Non
(iii) Oui
Méthode 2 : Quand ![]() est de dimension finie et muni d’une base, comment calculer
est de dimension finie et muni d’une base, comment calculer ![]() si
si ![]() est bilinéaire?
est bilinéaire?
Si ![]() ,
, ![]() , est une base de
, est une base de ![]() ,
, ![]() est complètement connue quand on connait les
est complètement connue quand on connait les ![]() :
:
si ![]() et
et ![]() sont les coordonnées de
sont les coordonnées de ![]() et
et ![]() dans cette base,
dans cette base,
![]() où
où ![]() .
.
Exemple : ![]() ,
, ![]() est la base canonique,
est la base canonique, ![]() est bilinéaire et
est bilinéaire et ![]() .
.
Donner l’expression de ![]() .
.
Réponse : ![]() .
.
Méthode 3 : Comment définir et utiliser la matrice d’une forme bilinéaire ?
![]() Si
Si ![]() est une forme bilinéaire sur
est une forme bilinéaire sur ![]() , si
, si ![]() est une base de
est une base de ![]() , la matrice de
, la matrice de ![]() dans
dans ![]()
est ![]() .
.
![]() Si
Si ![]() et
et ![]() sont les matrices de
sont les matrices de ![]() et
et ![]() dans
dans ![]() ,
, ![]() .
.
Exemple : ![]() est muni de la base canonique. Dire si
est muni de la base canonique. Dire si ![]() est une forme bilinéaire sur
est une forme bilinéaire sur ![]() et trouver sa matrice quand
et trouver sa matrice quand
(i) ![]()
(ii) ![]()
(iii) ![]() .
.
Réponse :
(i) Non : l’expression de ![]() comporte des carrés de coordonnées.
comporte des carrés de coordonnées.
(ii) Non : si on remplace ![]() par
par ![]() , le terme
, le terme ![]() est multiplié par
est multiplié par ![]() .
.
(iii) Oui : la matrice de ![]() est:
est:![]() .
.
Méthode 4 : Si ![]() est de dimension
est de dimension ![]() ,
, ![]() , si
, si ![]() et
et ![]() sont deux bases de
sont deux bases de ![]() , comment passer de l’expression de
, comment passer de l’expression de ![]() dans
dans ![]() à son expression dans
à son expression dans ![]() ?
?
Si ![]() est la matrice de passage de
est la matrice de passage de ![]() à
à ![]() , si
, si ![]() et
et ![]() ont pour matrices
ont pour matrices ![]() et
et ![]() dans
dans ![]() ,
, ![]()
et ![]() dans
dans ![]() , si
, si ![]() est la matrice de
est la matrice de ![]() dans
dans ![]() et
et ![]() sa matrice dans
sa matrice dans ![]() , on a:
, on a:
![]() ,
, ![]() , et
, et ![]() , donc
, donc ![]() .
.
Exemple : ![]() est muni de la base canonique
est muni de la base canonique ![]() ,
, ![]() . Ecrire l’expression de
. Ecrire l’expression de ![]() à l’aide des coordonnées de
à l’aide des coordonnées de ![]() et
et ![]() dans
dans ![]() où
où ![]() .
.
Réponse : ![]() et
et ![]() , donc
, donc
![]() , d’où:
, d’où:
![]() .
.
2. Produit scalaire, norme associée
Méthode 5 : Comment savoir si une application ![]() est un produit scalaire?
est un produit scalaire?
Pour que ![]() soit un produit scalaire, il faut et il suffit qu’elle soit:
soit un produit scalaire, il faut et il suffit qu’elle soit:
![]() bilinéaire
bilinéaire
![]() symétrique :
symétrique : ![]() ,
, ![]()
![]() définie positive :
définie positive : ![]() ,
, ![]() , et si
, et si ![]() , alors
, alors ![]() .
.
Méthode 6 : Comment définir et utiliser le produit scalaire canonique dans ![]() ?
?
On note ![]() la base canonique de
la base canonique de ![]() . Le produit scalaire canonique est défini par : si
. Le produit scalaire canonique est défini par : si ![]() appartiennent à
appartiennent à ![]() ,
, 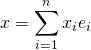 ,
, 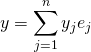 , alors
, alors
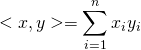 .
.
Les matrices de ![]() et
et ![]() dans la base canonique sont
dans la base canonique sont 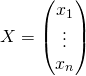 et
et
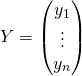 . L’expression matricielle du produit scalaire canonique est donc:
. L’expression matricielle du produit scalaire canonique est donc:
Dans ![]() :
: ![]() et
et ![]() . Le produit scalaire (canonique) de
. Le produit scalaire (canonique) de ![]() et
et ![]() est :
est :
(i) 4
(ii) 6
(iii) 0
Réponse : On a: ![]() , donc
, donc ![]() existe et
existe et ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Méthode 7 : Y a-t-il d’autres produits scalaires usuels que des produits scalaires définis sur ![]() ?
?
Oui. Par exemple, si ![]() est l’espace vectoriel des fonctions définies et continues sur l’intervalle
est l’espace vectoriel des fonctions définies et continues sur l’intervalle ![]() , à valeurs réelles, on définit un produit scalaire sur
, à valeurs réelles, on définit un produit scalaire sur ![]() en posant, pour
en posant, pour ![]() et
et ![]() dans
dans ![]() ,
,
![]() .
.
Exemple :
En posant ![]() , on définit un produit scalaire sur :
, on définit un produit scalaire sur :
(i) ![]() ?
?
(ii) ![]() est dérivable sur
est dérivable sur ![]() ?
?
Réponse :
(i) Non : en prenant ![]() si
si ![]() et
et ![]() , on a
, on a ![]() , mais
, mais ![]() ;
;
(ii) Oui : les fonctions dérivables sur [0,1] sont continues sur ![]() .
.
Méthode 8 : Comment calculer la norme d’un vecteur? Quelles sont les propriétés de la norme?
![]() Si
Si ![]() est muni d’un produit scalaire, la norme associée au produit scalaire est définie par :
est muni d’un produit scalaire, la norme associée au produit scalaire est définie par : ![]() .
.
pour tout
pour tout
pour tous
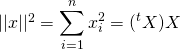 .
.Exemple : Dans ![]() ,
, ![]() et
et ![]() où
où ![]() . La norme de
. La norme de ![]() est
est ![]() .
.
Quelle est la valeur de ![]() ?
?
Réponse : ![]()
Méthode 9 : Quelles sont les relations d’égalité ou d’inégalité à connaître entre produit scalaire et norme?
![]()
![]() .
.
Cette relation permet de retrouver le produit scalaire à l’aide de la norme.
![]()
![]() .
.
Cette relation découle de ![]() et
et ![]() .
.
![]() Inégalité de Cauchy-Schwarz:
Inégalité de Cauchy-Schwarz: ![]() .
.
Les cas où l’égalité est obtenue dans cette inégalité sont:
![]() si et seulement si
si et seulement si ![]() ou
ou ![]() ,
, ![]() ;
;
![]() si et seulement si
si et seulement si ![]() ou
ou ![]() ,
, ![]() .
.
Exemple : Si ![]() est muni du produit scalaire
est muni du produit scalaire ![]() , alors on a:
, alors on a:
(i) : ![]() ?
?
(ii) : ![]()
![]() ?
?
(iii) : ![]()
![]() ?
?
(iv) : ![]()
![]() ?
?
3. Orthogonalité
Méthode 10 : ![]() est muni d’un produit scalaire. Quand peut-on parler d’orthogonalité entre éléments ou parties de
est muni d’un produit scalaire. Quand peut-on parler d’orthogonalité entre éléments ou parties de ![]() ?
?
![]() Si
Si ![]() et
et ![]() sont deux vecteurs de
sont deux vecteurs de ![]() , on calcule
, on calcule ![]() : si
: si ![]() , on dira que
, on dira que ![]() et
et ![]() sont orthogonaux (ou que
sont orthogonaux (ou que ![]() est orthogonal à
est orthogonal à ![]() , ou que
, ou que ![]() est orthogonal à
est orthogonal à ![]() ), et on notera
), et on notera ![]() ; sinon,
; sinon, ![]() et
et ![]() ne sont pas orthogonaux.
ne sont pas orthogonaux.
![]() Si
Si ![]() est un vecteur de
est un vecteur de ![]() et si
et si ![]() est une partie de
est une partie de ![]() ou une famille de vecteurs de
ou une famille de vecteurs de ![]() , on dira que
, on dira que ![]() est orthogonal à
est orthogonal à ![]() si
si ![]() est orthogonal à tout vecteur de
est orthogonal à tout vecteur de ![]() , et on notera
, et on notera ![]() .
.
En particulier, si ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() , si
, si ![]() est une famille génératrice de
est une famille génératrice de ![]() ,
, ![]() est orthogonal à
est orthogonal à ![]() si et seulement si
si et seulement si ![]() est orthogonal à
est orthogonal à ![]() .
.
![]() Si
Si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() , on dira que
, on dira que ![]() et
et ![]() sont orthogonales (ou que
sont orthogonales (ou que ![]() est orthogonale à
est orthogonale à ![]() ) si tout vecteur de
) si tout vecteur de ![]() est orthogonal à tout vecteur de
est orthogonal à tout vecteur de ![]() (ou si tout vecteur de
(ou si tout vecteur de ![]() est orthogonal à
est orthogonal à ![]() ), et on notera alors
), et on notera alors ![]() .
.
En particulier, si ![]() et
et ![]() sont deux sous-espaces vectoriels de
sont deux sous-espaces vectoriels de ![]() , si
, si ![]() est une famille génératrice de
est une famille génératrice de ![]() et
et ![]() est une famille génératrice de
est une famille génératrice de ![]() ,
, ![]() et
et ![]() sont orthogonaux si et seulement si
sont orthogonaux si et seulement si ![]() et
et ![]() sont orthogonales.
sont orthogonales.
Exemple : ![]() est muni du produit scalaire
est muni du produit scalaire ![]() ,
,
![]() ,
,
et ![]() , où
, où ![]() .
.
Pour quelles valeurs de ![]() a-t-on
a-t-on ![]() ?
?
Méthode 11 : ![]() est muni d’un produit scalaire. Quel est l’ensemble des vecteurs orthogonaux à un vecteur donné? à une partie donnée?
est muni d’un produit scalaire. Quel est l’ensemble des vecteurs orthogonaux à un vecteur donné? à une partie donnée?
![]() Si
Si ![]() , l’ensemble des vecteurs de
, l’ensemble des vecteurs de ![]() orthogonaux à
orthogonaux à ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() appelé l’orthogonal de
appelé l’orthogonal de ![]() et noté
et noté ![]() :
:
![]() . En particulier
. En particulier ![]() .
.
Pour tout ![]() de
de ![]() , on a:
, on a: ![]() , et si
, et si ![]() est une partie de
est une partie de ![]() ,
, ![]() équivaut à
équivaut à ![]() .
.
![]() Si
Si ![]() est une partie de
est une partie de ![]() , l’ensemble des vecteurs de
, l’ensemble des vecteurs de ![]() orhogonaux à
orhogonaux à ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() appelé l’orthogonal de
appelé l’orthogonal de ![]() et noté
et noté ![]() . En particulier
. En particulier ![]() .
.
On a encore ![]() , et si
, et si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() ,
, ![]() équivaut à
équivaut à ![]() (ou à
(ou à ![]() ). En prenant
). En prenant ![]() , on obtient
, on obtient ![]() .
.
![]() Si
Si ![]() est une partie finie,
est une partie finie, ![]() , alors
, alors ![]() .
.
Exemple :
![]() est muni du produit scalaire canonique,
est muni du produit scalaire canonique, ![]() .
.
Quelle est l’équation de ![]() ?
?
Réponse : ![]()
Méthode 12 : ![]() est muni d’un produit scalaire. Qu’est-ce qu’une famille orthogonale? une famille orthonormale?
est muni d’un produit scalaire. Qu’est-ce qu’une famille orthogonale? une famille orthonormale?
Une famille ![]() de vecteurs de
de vecteurs de ![]() est
est
![]() orthogonale si pour
orthogonale si pour ![]() ,
, ![]() est orthogonal à
est orthogonal à ![]() ;
;
![]() orthonormale si elle est orthogonale et si tous les vecteurs de la famille sont unitaires (c’est-à-dire de norme
orthonormale si elle est orthogonale et si tous les vecteurs de la famille sont unitaires (c’est-à-dire de norme ![]() ).
).
Une famille orthogonale formée de vecteurs tous non nuls est libre. Une famille orthonormale est libre.
Exemple :
![]() est muni du produit scalaire
est muni du produit scalaire ![]() .
.
La famille ![]() est orthonormale si et seulement si:
est orthonormale si et seulement si:
(i) ![]() et
et ![]() ?
?
(ii) ![]() ?
?
(iii) ![]() ?
?
Réponse : (ii)
Méthode 13 : ![]() est muni d’un produit scalaire. Comment exploiter l’orthogonalité?
est muni d’un produit scalaire. Comment exploiter l’orthogonalité?
![]() Pour montrer qu’un vecteur de
Pour montrer qu’un vecteur de ![]() est nul, on peut montrer qu’il est orthogonal à tous les vecteurs de
est nul, on peut montrer qu’il est orthogonal à tous les vecteurs de ![]() .
.
![]() Pour montrer qu’une famille est libre, on peut vérifier que les vecteurs qui la composent sont non nuls, et montrer qu’elle est orthogonale.
Pour montrer qu’une famille est libre, on peut vérifier que les vecteurs qui la composent sont non nuls, et montrer qu’elle est orthogonale.
![]() Si
Si ![]() et
et ![]() sont deux sous-espaces vectoriels de
sont deux sous-espaces vectoriels de ![]() orthogonaux,
orthogonaux, ![]() , la somme
, la somme ![]() est directe.
est directe.
![]() Si
Si ![]() est une famille orthonormale de
est une famille orthonormale de ![]() , pour tout
, pour tout ![]() de
de ![]() ,
, 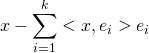 est
est
orthogonal à ![]() .
.
Exemple :
![]() est polynomiale à coefficients réels
est polynomiale à coefficients réels![]()
On suppose que ![]() et que
et que ![]() ,
,
![]() .
.
A-t-on ![]() ?
?
Réponse : Oui, on munit ![]() du produit scalaire défini par:
du produit scalaire défini par: ![]() ;
;
![]() est orthogonale à toutes les fonctions de
est orthogonale à toutes les fonctions de ![]() , donc
, donc ![]() .
.
Méthode 14 : Comment relier l’orthogonalité à la norme?
En utilisant le théorème de Pythagore: ![]() et
et ![]() sont orthogonaux si et seulement si
sont orthogonaux si et seulement si ![]() .
.
Exemple : ![]() est muni d’un produit scalaire,
est muni d’un produit scalaire, ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() ,
, ![]() un vecteur de
un vecteur de ![]() , et
, et ![]() un vecteur de
un vecteur de ![]() tel que:
tel que: ![]() .
.
Montrer que, pour tout vecteur ![]() de
de ![]() ,
, ![]() .
.
Réponse : si ![]() ,
, ![]() , donc
, donc ![]() ; en remarquant que
; en remarquant que ![]() et en utilisant le théorème de Pythagore,
et en utilisant le théorème de Pythagore,
![]() , donc
, donc ![]() .
.
4. Espaces euclidiens
Méthode 15 : Qu’est-ce qu’un espace euclidien? Quelle en est la principale propriété?
C’est un espace vectoriel sur ![]() de dimension finie, muni d’un produit scalaire.
de dimension finie, muni d’un produit scalaire.
La base canonique de ![]() est-elle orthonormée pour le produit scalaire canonique ?
est-elle orthonormée pour le produit scalaire canonique ?
Réponse : Oui
Méthode 16 : Si ![]() est euclidien, comment savoir qu’une famille de vecteurs de
est euclidien, comment savoir qu’une famille de vecteurs de ![]() est une b.o.n. (base orthonormée ou base orthonormale) de
est une b.o.n. (base orthonormée ou base orthonormale) de ![]() ?
?
Si ![]() , il suffit de vérifier que la famille a
, il suffit de vérifier que la famille a ![]() éléments et qu’elle est orthonormale.
éléments et qu’elle est orthonormale.
Exemple : ![]() est un espace euclidien
est un espace euclidien ![]() et
et ![]() sont deux sous-espaces vectoriels de
sont deux sous-espaces vectoriels de ![]() ,distincts de
,distincts de ![]() , supplémentaires:
, supplémentaires: ![]() .
.
![]() est une b.o.n. de
est une b.o.n. de ![]() ,
, ![]() est une b.o.n. de
est une b.o.n. de ![]() . Alors:
. Alors:
(i) ![]() est une b.o.n. de
est une b.o.n. de ![]() ?
?
(ii) ![]() est une b.o.n. de
est une b.o.n. de ![]() si et seulement si
si et seulement si ![]() ?
?
(iii) ![]() est une b.o.n. de
est une b.o.n. de ![]() si et seulement si
si et seulement si ![]() ?
?
Réponse : (iii) La famille a ![]() éléments et
éléments et ![]() puisque
puisque ![]() , tous les vecteurs sont de norme
, tous les vecteurs sont de norme ![]() , et elle est orthogonale si et seulement si
, et elle est orthogonale si et seulement si
![]() est orthogonal à
est orthogonal à ![]() .
.
Méthode 17 : Si ![]() est euclidien, comment construire une b.o.n. de
est euclidien, comment construire une b.o.n. de ![]() ?
?
![]() Si
Si ![]() est de dimension
est de dimension ![]() ,
, ![]() , si
, si ![]() est une base de
est une base de ![]() , on peut construire la b.o.n.
, on peut construire la b.o.n. ![]() déduite de
déduite de ![]() par le procédé de Schmidt:
par le procédé de Schmidt:
![]() et, pour
et, pour ![]() , si
, si
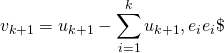 ,
, ![]() .
.
C’est l’unique b.o.n. de ![]() telle que, pour tout
telle que, pour tout ![]() tel que
tel que ![]() , on ait:
, on ait:
![]() et
et ![]() .
.
![]() Si
Si ![]() est de dimension
est de dimension ![]() ,
, ![]() , si
, si ![]() ,
, ![]() , est une famille orthonormale de
, est une famille orthonormale de ![]() , on peut la compléter en une base orthonormée
, on peut la compléter en une base orthonormée ![]() de
de ![]() .
.
Exemple :
Dans ![]() muni du produit scalaire canonique, on donne les vecteurs
muni du produit scalaire canonique, on donne les vecteurs
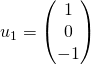 ,
, 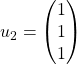 ,
, 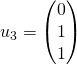 , qui forment une base
, qui forment une base ![]() de
de ![]() .
.
La b.o.n. ![]() déduite de
déduite de ![]() par le procédé de Schmidt est:
par le procédé de Schmidt est:
(i) 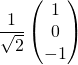 ,
, 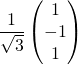 ,
, 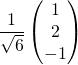 ?
?
(ii) 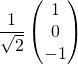 ,
, 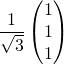 ,
, 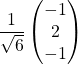 ?
?
Réponse : (ii)
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
Méthode 18 : Comment utilise-t-on les bases orthonormées?
Si ![]() est une base orthonormée de
est une base orthonormée de ![]() ,
,
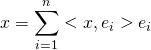 et
et 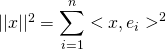 ;
;![]() .
.
Exemple : ![]() est muni du produit scalaire canonique.
est muni du produit scalaire canonique.
Si ![]() et
et
![]() ,
, ![]() est une b.o.n. de
est une b.o.n. de ![]() .
.
Si ![]() , les coordonnées de
, les coordonnées de ![]() dans
dans ![]() sont:
sont:
(i) ![]() ?
?
(ii) ![]() ?
?
Réponse : (ii)
Méthode 19 : Dans un espace euclidien, comment changer de b.o.n.? Qu’est-ce qu’une matrice orthogonale?
![]() Si
Si ![]() et
et ![]() sont deux b.o.n. de
sont deux b.o.n. de ![]() , si
, si ![]() est la matrice de passage de
est la matrice de passage de ![]() à
à ![]() , alors
, alors ![]() . On a donc
. On a donc ![]() .
.
![]() Une matrice carrée inversible
Une matrice carrée inversible ![]() qui vérifie
qui vérifie ![]() est une matrice orthogonale.
est une matrice orthogonale.
![]() Si
Si ![]() est une matrice orthogonale, si
est une matrice orthogonale, si ![]() est une b.o.n. de
est une b.o.n. de ![]() ,
, ![]() est la matrice de passage de
est la matrice de passage de ![]() à une base
à une base ![]() de
de ![]() ; alors,
; alors, ![]() est une base orthonormée de
est une base orthonormée de ![]() .
.
![]() Une matrice est orthogonale si et seulement si c’est une matrice de passage entre deux b.o.n. de
Une matrice est orthogonale si et seulement si c’est une matrice de passage entre deux b.o.n. de ![]() .
.
Exemple :
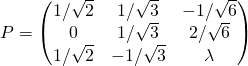 .
.
(i) ![]() est orthogonale si et seulement si
est orthogonale si et seulement si ![]() ?
?
(ii) ![]() est orthogonale si et seulement si
est orthogonale si et seulement si ![]() ?
?
(iii) ![]() n’est orthogonale pour aucun
n’est orthogonale pour aucun ![]() ?
?
Réponse : (i)
Méthode 20 : Dans un espace euclidien, quelles sont les propriétés des sous-espaces orthogonaux?
![]() Si
Si ![]() et
et ![]() sont deux sous-espaces vectoriels orthogonaux d’un espace euclidien
sont deux sous-espaces vectoriels orthogonaux d’un espace euclidien ![]() , alors:
, alors:
(i) ![]() ;
;
(ii) si ![]() , alors
, alors ![]() ;
;
![]() (i) Si
(i) Si ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() , alors
, alors ![]() ;
;
(ii) Si ![]() et
et ![]() , alors
, alors ![]() :
: ![]() est le supplémentaire orthogonal de
est le supplémentaire orthogonal de ![]() .
.
Exemple : ![]() est un espace euclidien de dimension
est un espace euclidien de dimension ![]() ,
, ![]() , muni d’une b.o.n.
, muni d’une b.o.n. ![]() .
.
![]() . Trouver
. Trouver ![]() .
.
Réponse : Si ![]() , on a
, on a ![]() et
et ![]() , donc
, donc ![]() .
.
Améliorez votre niveau de maths en travaillant sur les cours en ligne de maths en ECS2 qui suivent :

