Chapitres Maths en ECS2
Cours : Calcul différentiel en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Fonctions partielles, fonctions C1
1. Fonctions partielles, dérivées partielles et gradient
Méthode 1 : Si ![]() , si
, si ![]() appartient à
appartient à ![]() ,comment définir les applications partielles de
,comment définir les applications partielles de ![]() en
en ![]() ?
?
![]() Si
Si ![]() , la première application partielle de
, la première application partielle de ![]() en
en ![]() est
est ![]() définie par:
définie par: ![]() , et la deuxième application partielle de
, et la deuxième application partielle de ![]() en
en ![]() est
est ![]() définie par:
définie par: ![]() .
.
![]() Si
Si ![]() ,
, ![]() , pour
, pour ![]() , la
, la ![]() application partielle de
application partielle de ![]() en
en ![]() est
est ![]() définie par
définie par ![]() (
(![]() et
et
![]() ).
).
On a donc ![]() .
.
Exemple : La fonction ![]() est définie par
est définie par ![]() , et
, et ![]() .
.
Calculer ![]() ,
, ![]() ,
, ![]() .
.
Réponse : ![]() ,
, ![]() , et
, et ![]() .
.
Méthode 2 : Si ![]() , si
, si ![]() et si
et si ![]() , quand peut-on dire que
, quand peut-on dire que ![]() admet une
admet une ![]() dérivée partielle en
dérivée partielle en ![]() ?
?
![]() admet une
admet une ![]() dérivée partielle en
dérivée partielle en ![]() , notée
, notée ![]() , si la
, si la ![]() application partielle en
application partielle en ![]() est dérivable en
est dérivable en ![]() , et alors
, et alors
![]() .
.
Exemple : Soit ![]() telle que
telle que ![]() , et
, et ![]() . Alors
. Alors
(i) : ![]() admet-elle des dérivées partielles
admet-elle des dérivées partielles ![]() pour
pour ![]() quelque soit la valeur de
quelque soit la valeur de ![]() ?
?
(ii) : ![]() et
et ![]() existent quelque soit la valeur de
existent quelque soit la valeur de ![]() , mais
, mais ![]() n’est définie que si
n’est définie que si ![]() ?
?
(iii) : ![]() et
et ![]() existent pour tout
existent pour tout ![]() de
de ![]() , mais
, mais ![]() n’est définie que si
n’est définie que si ![]() ?
?
Réponse :
(i) Faux
(ii) Faux
(iii) Vrai
Méthode 3 : Comment calculer des dérivées partielles en utilisant un taux d’accroissement ?
Pour calculer la ![]() dérivée partielle de
dérivée partielle de ![]() en
en ![]() , il suffit d’écrire le taux d’accroissement de
, il suffit d’écrire le taux d’accroissement de ![]() en
en ![]() :
:
![]()
![]()
![]() .
.
Si ![]() a une limite réelle quand
a une limite réelle quand ![]() ,
, ![]() existe et
existe et ![]() .
.
En posant ![]() , on peut aussi écrire
, on peut aussi écrire ![]() sous la forme:
sous la forme:
![]()
![]()
![]() ,
,
et si ![]() a une limite réelle quand
a une limite réelle quand ![]() ,
, ![]() existe et
existe et ![]() .
.
Exemple : Dans ![]() ,
, ![]() , et
, et ![]() est une fonction de
est une fonction de ![]() dans
dans ![]() telle que
telle que ![]() existe.
existe.
On définit ![]() par
par ![]() .
.
Montrer que ![]() existe et calculer
existe et calculer ![]() à l’aide de
à l’aide de ![]() .
.
Réponse : On forme le taux d’accroissement de ![]() en
en ![]() :
:
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Méthode 4 : Si ![]() est une fonction définie sur
est une fonction définie sur ![]() à valeurs dans
à valeurs dans ![]() , comment définir, pour
, comment définir, pour ![]() , la
, la ![]() dérivée partielle de
dérivée partielle de ![]() ? Comment en calculer l’expression ?
? Comment en calculer l’expression ?
Si pour tout ![]() de
de ![]() ,
, ![]() existe, on peut définir la fonction
existe, on peut définir la fonction ![]() qui à tout
qui à tout ![]() de
de ![]()
associe ![]() ;
; ![]() est alors la
est alors la ![]() dérivée partielle de
dérivée partielle de ![]() .
.
Pour tout ![]() de
de ![]() ,
, ![]()
![]() , ou encore, pour tout
, ou encore, pour tout ![]() de
de ![]() ,
, ![]()
![]() .
.
Pour calculer l’expression de ![]() à partir de l’expression de
à partir de l’expression de ![]() , on considère
, on considère ![]() comme des constantes, et on dérive par rapport à la variable
comme des constantes, et on dérive par rapport à la variable ![]() .
.
Exemple : Soit ![]() telle que
telle que ![]() . Les dérivées partielles de
. Les dérivées partielles de ![]() sont données par:
sont données par:
(i) ![]() ,
, ![]() , et
, et ![]() ?
?
(ii) ![]() ,
, ![]() , et
, et ![]() ?
?
(iii) ![]() ,
, ![]() , et
, et ![]() ?
?
Réponse :
(i) Non: ![]() ,
, ![]() , et
, et ![]() .
.
(ii) Oui.
(iii) Non: ![]() ,
, ![]() , et
, et ![]() .
.
Méthode 5 : Quelles opérations peut-on faire sur les dérivées partielles ?
Elles sont analogues aux opérations que l’on peut faire sur les dérivées: si ![]() et
et ![]() sont deux fonctions définies sur
sont deux fonctions définies sur ![]() à valeurs réelles, si
à valeurs réelles, si ![]() appartient à
appartient à ![]() , et si pour
, et si pour ![]() ,
, ![]() et
et ![]() existent,
existent,
![]() pour tout
pour tout ![]() réel,
réel, ![]() existe et
existe et ![]() ;
;
![]()
![]() existe et
existe et ![]() ;
;
![]()
![]() existe et
existe et ![]() ;
;
![]() si
si ![]() ,
, ![]() existe et
existe et ![]() ;
;
![]() si
si ![]() est dérivable en
est dérivable en ![]() ,
, ![]() existe et
existe et ![]() .
.
Exemple : Si ![]() ,
, ![]() . Alors, pour tout
. Alors, pour tout ![]() de
de ![]() ,
,
(i) ![]() ?
?
(ii) ![]() ?
?
(iii) ![]() ?
?
Réponse : (i) Non: ![]() ?\\
?\\
(ii) Non: ![]() ?\\
?\\
(iii) Oui.
Méthode 6 : Qu’est-ce que le gradient d’une fonction ![]() définie sur
définie sur ![]() à valeurs dans
à valeurs dans ![]() ?
?
La fonction ![]() admet un gradient en un point
admet un gradient en un point ![]() de
de ![]() si pour tout
si pour tout ![]() de
de ![]() ,
, ![]() existe. Alors le gradient de
existe. Alors le gradient de ![]() en
en ![]() , noté
, noté ![]() , est l’élément de
, est l’élément de ![]() égal à
égal à ![]() .
.
Exemple : On donne ![]() , telle que
, telle que ![]() . Calculer
. Calculer ![]() .
.
Réponse : ![]()
![]() .
.
2. Fonctions  , développement limité à l’ordre
, développement limité à l’ordre 
Méthode 7 : Qu’est-ce qu’une fonction de classe ![]() sur
sur ![]() ?
?
Une fonction ![]() est de classe
est de classe ![]() sur
sur ![]() si, pour tout
si, pour tout ![]() de
de ![]() ,
, ![]() admet une dérivée partielle
admet une dérivée partielle ![]() définie sur
définie sur ![]() et continue sur
et continue sur ![]() .
.
Exemple : Montrer que la fonction ![]() définie par
définie par ![]() est
est ![]() sur
sur ![]() .
.
Réponse : ![]() et
et ![]() ;
; ![]() et
et ![]() sont des fonctions polynomiales, donc continues sur
sont des fonctions polynomiales, donc continues sur ![]() , donc
, donc ![]() est
est ![]() sur
sur ![]() .
.
Méthode 8 : Comment justifier sans calculs qu’une fonction définie sur ![]() est
est ![]() sur
sur ![]() ?
?
![]() Une fonction constante est
Une fonction constante est ![]() sur
sur ![]() .
.
![]() Si
Si ![]() et
et ![]() sont
sont ![]() sur
sur ![]() , si
, si ![]() est un réel,
est un réel, ![]() ,
, ![]() , et
, et ![]() sont
sont ![]() sur
sur ![]() ;
;
si pour tout ![]() de
de ![]() ,
, ![]() ,
, ![]() est
est ![]() sur
sur ![]() .
.
![]() Les fonctions polynomiales et les fonctions rationnelles définies sur
Les fonctions polynomiales et les fonctions rationnelles définies sur ![]() sont
sont ![]() sur
sur ![]() .
.
![]() Si
Si ![]() est
est ![]() sur
sur ![]() à valeurs dans un intervalle
à valeurs dans un intervalle ![]() de
de ![]() , et si
, et si ![]() est
est ![]() sur
sur ![]() ,
, ![]() est
est ![]() sur
sur ![]() .
.
![]() Si
Si ![]() sont des fonctions définies sur un intervalle
sont des fonctions définies sur un intervalle ![]() de
de ![]() à valeurs réelles, de classe
à valeurs réelles, de classe ![]() sur
sur ![]() , si
, si ![]() est de classe
est de classe ![]() sur
sur ![]() , alors la fonction
, alors la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
![]() Si
Si ![]() sont des fonctions définies sur
sont des fonctions définies sur ![]() à valeurs réelles, de classe
à valeurs réelles, de classe ![]() sur
sur ![]() , et si
, et si ![]() est de classe
est de classe ![]() sur
sur ![]() , la fonction de
, la fonction de ![]() dans
dans ![]() qui à
qui à ![]() associe
associe ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Exemple : On donne la fonction ![]() telle que
telle que ![]() .
.
Justifier que ![]() est
est ![]() sur
sur ![]() .
.
Réponse : La fonction ![]() est rationnelle et définie sur
est rationnelle et définie sur ![]() , donc elle est
, donc elle est ![]() sur
sur ![]() , et la fonction exponentielle est
, et la fonction exponentielle est ![]() sur
sur ![]() , donc
, donc ![]() est
est ![]() sur
sur ![]() .
.
Méthode 9 : Comment définir un développement limité à l’ordre ![]() (
(![]() ) pour une fonction de
) pour une fonction de ![]() dans
dans ![]() ?
?
![]() Si
Si ![]() est une fonction de
est une fonction de ![]() dans
dans ![]() et si
et si ![]() , on dira que
, on dira que ![]() admet un
admet un ![]() au point
au point ![]() s’il existe des réels
s’il existe des réels ![]() tels que, si
tels que, si ![]() ,
, ![]()
![]() où
où ![]() est continue en
est continue en ![]() et
et ![]() .
.
![]() On peut dire aussi:
On peut dire aussi: ![]() admet un
admet un ![]() en
en ![]() s’il existe des réels
s’il existe des réels ![]() tels que, pour
tels que, pour ![]() ,
, ![]()
![]() où
où ![]() quand
quand ![]() ,
, ![]() .
.
Exemple : La fonction ![]() est définie par
est définie par ![]() .
.
Montrer que ![]() admet un
admet un ![]() en tout point de
en tout point de ![]() .
.
Méthode 10 : Si une fonction ![]() admet un
admet un ![]() en un point
en un point ![]() de
de ![]() ,comment en prévoir les coefficients ? Et comment savoir si une fonction
,comment en prévoir les coefficients ? Et comment savoir si une fonction ![]() admet un
admet un ![]() en un point de
en un point de ![]() ?
?
![]() Si
Si ![]() admet un
admet un ![]() en
en ![]() ,
, ![]() admet des dérivées partielles
admet des dérivées partielles ![]() pour
pour ![]() , qui sont les coefficients du
, qui sont les coefficients du ![]() :
: ![]()
![]()
![]() où
où ![]() et
et ![]() est continue en
est continue en ![]() .
.
Donc le ![]() de
de ![]() en
en ![]() , quand il existe, est unique.
, quand il existe, est unique.
![]() Si
Si ![]() est de classe
est de classe ![]() sur
sur ![]() ,
, ![]() admet en tout point de
admet en tout point de ![]() un
un ![]() donné par:
donné par: ![]()
![]() où
où ![]() et
et ![]() est continue en
est continue en ![]() .
.
Exemple : On donne ![]() définie par:
définie par: ![]() . Justifier que
. Justifier que ![]() admet un
admet un ![]() en tout point de
en tout point de ![]() et écrire ce
et écrire ce ![]() .
.
Réponse : ![]() est
est ![]() sur
sur ![]() , donc admet un
, donc admet un ![]() en tout point de
en tout point de ![]() :
:
![]()
![]()
![]()
![]() où
où ![]() et
et ![]() est continue en
est continue en ![]() .
.
Méthode 11 : Quels renseignements sur ![]() peut-on déduire d’un
peut-on déduire d’un ![]() de
de ![]() en un point
en un point ![]() de
de ![]() ?
?
![]() Si
Si ![]() admet un
admet un ![]() en
en ![]() ,
, ![]() est continue en
est continue en ![]() . Donc une fonction de classe
. Donc une fonction de classe ![]() sur
sur ![]() est
est ![]() sur
sur ![]() .
.
![]() La fonction
La fonction ![]() qui à
qui à ![]() associe
associe 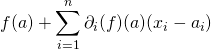 est une fonction affine (appelée fonction affine tangente à
est une fonction affine (appelée fonction affine tangente à ![]() en
en ![]() ), et
), et ![]() est une approximation de
est une approximation de ![]() quand
quand ![]() est petit, c’est-à-dire quand
est petit, c’est-à-dire quand ![]() est voisin de
est voisin de ![]() .
.
Exemple : On donne ![]() telle que
telle que ![]() . Donner une valeur approchée de
. Donner une valeur approchée de ![]() .
.
Réponse : La fonction ![]() est polynomiale, donc
est polynomiale, donc ![]() ,
, ![]() ,
, ![]() et
et ![]() , donc
, donc ![]() ; en prenant
; en prenant ![]() et en utilisant le
et en utilisant le ![]() de
de ![]()
en ![]() , on trouve
, on trouve ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
3. Dérivées directionnelles et autres dérivées
Méthode 12 : Si ![]() , si
, si ![]() et
et ![]() appartiennent à
appartiennent à ![]() , comment interpréter la fonction
, comment interpréter la fonction ![]() définie par
définie par ![]() ? Comment l’utiliser?
? Comment l’utiliser?
![]() En utilisant les points et les vecteurs de
En utilisant les points et les vecteurs de ![]() ,
, ![]() équivaut à
équivaut à ![]() .
.
Quand ![]() décrit
décrit ![]() ,
, ![]() décrit la droite
décrit la droite ![]() passant par
passant par ![]() dirigée par
dirigée par ![]() .
.
![]() En particulier, si
En particulier, si ![]() est de norme
est de norme ![]() ,
, ![]() constitue un repère (ortho)normé de
constitue un repère (ortho)normé de ![]() , et
, et ![]() est l’abscisse du point
est l’abscisse du point ![]() dans ce repère;
dans ce repère;
![]() donne la valeur de
donne la valeur de ![]() au point de
au point de ![]() d’abscisse
d’abscisse ![]() .
.
![]() Si on veut étudier la restriction de
Si on veut étudier la restriction de ![]() à la droite
à la droite ![]() , utiliser la fonction
, utiliser la fonction ![]() permet de se ramener à une fonction d’une variable.
permet de se ramener à une fonction d’une variable.
Exemple :
![]() est une fonction de
est une fonction de ![]() dans
dans ![]() , de classe
, de classe ![]() sur
sur ![]() . On note
. On note ![]() et
et ![]() , et on pose, pour
, et on pose, pour ![]() ,
, ![]() .
.
Exprimer ![]() à l’aide de
à l’aide de ![]() , montrer que
, montrer que ![]() est dérivable sur
est dérivable sur ![]() et calculer
et calculer ![]() .
.
Réponse : ![]() ; comme
; comme ![]() est
est ![]() sur
sur ![]() ,
, ![]() est dérivable sur
est dérivable sur ![]() , donc
, donc ![]() l’est aussi et
l’est aussi et ![]() , donc
, donc ![]() .
.
Méthode 13 : Comment dériver la fonction de ![]() dans
dans ![]() qui à
qui à ![]() associe
associe ![]() quand
quand ![]() est
est ![]() sur
sur ![]() et
et ![]() appartiennent à
appartiennent à ![]() ?
?
Si ![]() est
est ![]() sur
sur ![]() , la fonction
, la fonction ![]() est
est ![]() sur
sur ![]() et
et ![]() .
.
Exemple :
On donne ![]() ,
, ![]() ,
, ![]() et pour
et pour ![]() réel,
réel, ![]() .
.
Calculer ![]() :
:
(i) sans calculer l’expression de ![]() ;
;
(ii) en calculant d’abord l’expression de ![]() .
.
Méthode 14 : Si ![]() est
est ![]() sur
sur ![]() , si
, si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() , qu’est-ce que la dérivée de
, qu’est-ce que la dérivée de ![]() en
en ![]() dans la direction
dans la direction ![]() ? Comment l’utiliser?
? Comment l’utiliser?
![]() La dérivée de
La dérivée de ![]() en
en ![]() dans la direction
dans la direction ![]() est la dérivée de
est la dérivée de ![]() en
en ![]() : elle vaut donc
: elle vaut donc ![]() .
.
![]() On peut utiliser la dérivée directionnelle en
On peut utiliser la dérivée directionnelle en ![]() pour calculer
pour calculer ![]() : il peut être plus simple de dériver
: il peut être plus simple de dériver ![]() par rapport à
par rapport à ![]() que de calculer
que de calculer
les dérivées partielles de ![]() .
.
![]() Si
Si ![]() , l’inégalité de Cauchy-Schwarz donne:
, l’inégalité de Cauchy-Schwarz donne: ![]() , et l’ égalité est obtenue
, et l’ égalité est obtenue
dans l’inégalité de droite quand ![]() et
et ![]() sont liés de même sens, dans l’inégalité de gauche quand ils sont liés de sens contraires.
sont liés de même sens, dans l’inégalité de gauche quand ils sont liés de sens contraires.
Donc, si ![]() , la dérivée de
, la dérivée de ![]() en
en ![]() dans la direction
dans la direction ![]() est maximale quand
est maximale quand ![]() a la direction de
a la direction de ![]() , cette variation est minimale (maximale négativement) quand
, cette variation est minimale (maximale négativement) quand ![]()
a la direction opposée à celle de ![]() .
.
Donc, si ![]() , l’augmentation de
, l’augmentation de ![]() à partir de
à partir de ![]() est maximale dans la direction de
est maximale dans la direction de ![]() , la diminution de
, la diminution de ![]() à partir de
à partir de ![]() est maximale dans la direction opposée
est maximale dans la direction opposée
à celle de ![]() (une diminution étant une augmentation négative).
(une diminution étant une augmentation négative).
S’il est non nul, le gradient de ![]() en
en ![]() , représenté comme un vecteur d’origine
, représenté comme un vecteur d’origine ![]() , est donc orienté dans le sens des
, est donc orienté dans le sens des ![]() croissants.
croissants.
Exemple : Calculer, en utilisant la dérivée directionnelle, le gradient de ![]() quand
quand 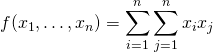 .
.
Méthode 15 : Si ![]() est un intervalle de
est un intervalle de ![]() , comment dériver la fonction
, comment dériver la fonction ![]() quand
quand ![]() où
où ![]() sont des fonctions de classe
sont des fonctions de classe ![]() sur
sur ![]() à valeurs réelles et
à valeurs réelles et ![]() une fonction de classe
une fonction de classe ![]() sur
sur ![]() ?
?
![]() On a vu que si, pour tout
On a vu que si, pour tout ![]() de
de ![]() ,
, ![]() est affine:
est affine: ![]() , alors
, alors ![]() et
et
![]()

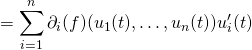
![]() En général, on a de même:
En général, on a de même: 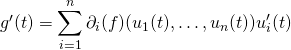
Exemple :
![]() est donnée par:
est donnée par: ![]() , et
, et ![]() est définie par:
est définie par: ![]() où
où ![]() est une fonction
est une fonction
de classe ![]() sur
sur ![]() , à valeurs réelles. Justifier que
, à valeurs réelles. Justifier que ![]() est
est ![]() sur
sur ![]() et calculer
et calculer ![]() .
.
Méthode 16 : Comment calculer les dérivées partielles de la fonction ![]() qui à
qui à ![]() associe
associe ![]() quand
quand
![]() sont
sont ![]() sur
sur ![]() à valeurs réelles et
à valeurs réelles et ![]() est
est ![]() sur
sur ![]() ?
?
Pour ![]() , en considérant les
, en considérant les ![]() pour
pour ![]() comme des constantes et
comme des constantes et ![]() comme la variable,
comme la variable,
et en appliquant le résultat précédent, on obtient:
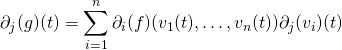
Exemple :
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() . On définit
. On définit ![]() par:
par:
![]() . Calculer les dérivées partielles de
. Calculer les dérivées partielles de ![]() à l’aide de celles de
à l’aide de celles de ![]() .
.
4. Extremas, points critiques
Méthode 17 : Comment différencier un extremum local d’un extremum global ?
![]()
![]() admet en un point
admet en un point ![]() de
de ![]() un maximum global si pour tout
un maximum global si pour tout ![]() de
de ![]() ,
, ![]()
(![]() admet en
admet en ![]() un minimum global si pour tout
un minimum global si pour tout ![]() de
de ![]() ,
, ![]() );
);
![]()
![]() admet en
admet en ![]() un maximum local s’il existe
un maximum local s’il existe ![]() tel que, si
tel que, si ![]() ,
, ![]() (
(![]() admet en
admet en ![]() un minimum local s’il
un minimum local s’il
existe ![]() tel que, si
tel que, si ![]() ,
, ![]() ).
).
![]() Si
Si ![]() admet en
admet en ![]() un maximum (ou un minimum) global, elle admet en
un maximum (ou un minimum) global, elle admet en ![]() un maximum (ou un minimum) local.
un maximum (ou un minimum) local.
Exemple :
![]() est la fonction de
est la fonction de ![]() dans
dans ![]() définie par:
définie par: ![]() . Montrer que
. Montrer que ![]() admet en
admet en ![]() un maximum local. Est-ce un maximum
un maximum local. Est-ce un maximum
global?
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 18 : Si ![]() est de classe
est de classe ![]() sur
sur ![]() , comment trouver les points où une fonction admet un extremum (local ou global)?
, comment trouver les points où une fonction admet un extremum (local ou global)?
![]() Si
Si ![]() est de classe
est de classe ![]() sur
sur ![]() et si
et si ![]() admet en un point
admet en un point ![]() de
de ![]() un extremum local, alors
un extremum local, alors
![]() .
.
![]() Les points
Les points ![]() de
de ![]() telsque
telsque ![]() sont les points critiques. Les points critiques sont les points candidats à l’extremum
sont les points critiques. Les points critiques sont les points candidats à l’extremum
(local ou global).
En un point critique, toutes les dérivées directionnelles sont nulles.
Exemples : On donne la fonction ![]() telle que
telle que ![]() . En quels points de
. En quels points de ![]() la fonction
la fonction ![]() peut-elle présenter un extremum?
peut-elle présenter un extremum?
On donne la fonction ![]() telle que
telle que ![]() . Cette fonction admet-elle un extremum (local ou global) sur
. Cette fonction admet-elle un extremum (local ou global) sur ![]() ?
?
Méthode 19 : Si ![]() est de classe
est de classe ![]() sur
sur ![]() , comment savoir si un point critique de
, comment savoir si un point critique de ![]() est un point où
est un point où ![]() admet un extremum (local ou global) ?
admet un extremum (local ou global) ?
Si ![]() est un point critique, on peut former
est un point critique, on peut former ![]() et en étudier le signe, pour tout
et en étudier le signe, pour tout ![]() de
de ![]() ou pour tout
ou pour tout ![]() de
de ![]() voisin de
voisin de ![]() .
.
Exemple : Si ![]() est définie par
est définie par ![]() ,
, ![]() admet un unique point critique
admet un unique point critique ![]() . La fonction
. La fonction ![]() admet-elle un
admet-elle un
extremum (local ou global) sur ![]() ?
?
Réponse : ![]() ne peut admettre un extremum qu’au point critique
ne peut admettre un extremum qu’au point critique ![]() ; on trouve
; on trouve ![]() . Pour tout
. Pour tout ![]() réel,
réel, ![]() et
et
![]() ; pour tout
; pour tout ![]() ,
, ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
On a ![]() et
et ![]() , donc quelque soit le réel strictement positif
, donc quelque soit le réel strictement positif ![]() , il existe
, il existe ![]() et
et ![]() réels
réels
tels que ![]() et
et ![]() , pour lesquels on a
, pour lesquels on a ![]() et
et ![]() .
.
Donc le point critique ![]() n’est pas un extremum local; ce n’est pas, à plus forte raison, un extremum global.
n’est pas un extremum local; ce n’est pas, à plus forte raison, un extremum global.
Chaque chapitre de maths au programme d’ECS2 doit être travaillé et parfaitement acquis avant les concours post-prépa, les cours en ligne et les cours de maths particulier permettent ainsi de vérifier ses connaissances et d’identifier ses difficultés :

