Chapitres Maths en ECS2
Cours : Compléments sur les variables aléatoires réelles en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Ce cours en ligne consacré aux compléments sur les variables aléatoire réelles en ECS2 représente une précieuse ressource pour vous aider à avancer tout au long de votre année en classe préparatoire aux grandes écoles. N’hésitez pas à enrichir votre apprentissage en combinant nos cours gratuits en ligne avec nos cours de soutien en maths.
Valeurs propres & Vecteurs propres et Probas à densité
1. Généralités sur les variables aléatoires réelles
Méthode 1 : Comment utiliser les tribus?
![]() Un espace probabilisable est un couple
Un espace probabilisable est un couple ![]() où
où ![]() est une tribu sur
est une tribu sur ![]() : c’est la tribu des événements.
: c’est la tribu des événements.
![]() Sur
Sur ![]() , la tribu des Boréliens est la plus petite tribu contenant tous les intervalles de
, la tribu des Boréliens est la plus petite tribu contenant tous les intervalles de ![]() .
.
On peut dire aussi que la tribu des Boréliens est la plus petite tribu contenant tous les intervalles du type ![]() ,
, ![]() , puisqu’on peut écrire tous les intervalles de
, puisqu’on peut écrire tous les intervalles de ![]() à l’aide d’intervalles de ce type et des opérations passage au complémentaire, intersection au plus dénombrable, union au plus dénombrable.
à l’aide d’intervalles de ce type et des opérations passage au complémentaire, intersection au plus dénombrable, union au plus dénombrable.
![]() Une application
Une application ![]() est une variable aléatoire réelle sur
est une variable aléatoire réelle sur ![]() si, pour tout
si, pour tout ![]() ,
, ![]() .
.
![]() Si
Si ![]() est une variable aléatoire sur
est une variable aléatoire sur ![]() , la tribu
, la tribu ![]() liée à
liée à ![]() est la plus petite tribu contenant les
est la plus petite tribu contenant les ![]() ,
, ![]() .
.
Alors, pour tout intervalle ![]() ,
, ![]() , et même pour tout Borélien
, et même pour tout Borélien ![]() ,
, ![]() .
.
![]() Utiliser les tribus permet de faire les opérations ensemblistes indifféremment sur les Boréliens ou sur les éléments de
Utiliser les tribus permet de faire les opérations ensemblistes indifféremment sur les Boréliens ou sur les éléments de ![]() , comme on le trouve le plus commode,
, comme on le trouve le plus commode,
on passe des uns aux autres à l’aide de ![]() .
.
On ne cherche pas, en général, à décrire tous les éléments d’une tribu; on s’en sert, tout simplement.
Exemple : ![]() est une variable aléatoire réelle sur
est une variable aléatoire réelle sur ![]() . Est-ce que
. Est-ce que ![]() appartient à
appartient à ![]() ?
?
Méthode 2 : Comment montrer que ![]() est une variable aléatoire réelle?
est une variable aléatoire réelle?
On vérifie d’abord que ![]() est une application de
est une application de ![]() dans
dans ![]() . Puis on peut
. Puis on peut
![]() Montrer que, pour tout
Montrer que, pour tout ![]() réel,
réel, ![]() est un événement;
est un événement;
![]() Remarquer que
Remarquer que ![]() s’écrit comme combinaison linéaire, somme, ou produit de variables réelles, et utiliser: si
s’écrit comme combinaison linéaire, somme, ou produit de variables réelles, et utiliser: si ![]() et
et ![]() sont deux variables réelles sur
sont deux variables réelles sur ![]() , si
, si ![]() et
et ![]() sont deux réels, alors
sont deux réels, alors ![]() ,
, ![]() ,
, ![]() sont des variables aléatoires réelles sur
sont des variables aléatoires réelles sur ![]() .
.
Exemple : ![]() est une v.a.r. strictement positive sur
est une v.a.r. strictement positive sur ![]() . On pose
. On pose ![]() .
.
![]() est-elle une v.a.r.?
est-elle une v.a.r.?
Réponse : Pour tout ![]() réel,
réel, ![]() , et comme
, et comme ![]() est une v.a.r.,
est une v.a.r., ![]() , donc
, donc ![]() est une v.a.r..
est une v.a.r..
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Recherches des valeurs et vecteurs propres
Méthode 3 : Comment peut-on calculer sur des sommes infinies?
Si la série 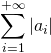 converge, alors
converge, alors ![]() est un réel que l’on peut calculer, comme
est un réel que l’on peut calculer, comme
lorsque la somme est finie, en changeant l’ordre des termes (commutativité généralisée), ou en regroupant certains termes (associativité généralisée).
De même, si la somme double ![]() converge, on peut calculer
converge, on peut calculer ![]() , et pour ce faire,
, et pour ce faire,
on peut changer l’ordre des termes ou regrouper certains termes comme dans le cas des sommes finies.
Exemple : Calculer ![]() , où
, où ![]() .
.
Réponse : Les termes de la somme sont positifs. Sous réserve d’existence des sommes infinies, on a:
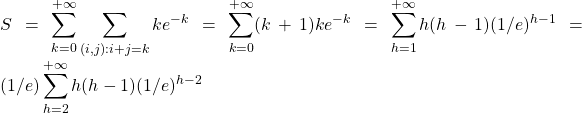 .
.
Comme ![]() , cette dernière somme est un réel, à savoir
, cette dernière somme est un réel, à savoir ![]() . Donc toutes les sommes écrites convergent, et
. Donc toutes les sommes écrites convergent, et
![]()
Méthode 4 : ![]() est une v.a.r. discrète sur
est une v.a.r. discrète sur ![]() . Comment savoir si
. Comment savoir si ![]() admet une espérance et la calculer? si
admet une espérance et la calculer? si ![]() est centrée?
est centrée?
![]() Si
Si ![]() est fini,
est fini, ![]() admet une espérance:
admet une espérance: ![]() .
.
![]() Sinon,
Sinon, ![]() admet une espérance si et seulement si
admet une espérance si et seulement si ![]() converge, et si
converge, et si
c’est le cas ![]() .
.
![]() Si
Si ![]() admet une espérance:
admet une espérance: 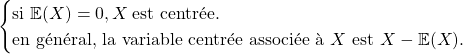
Exemple : ![]() est une v.a.r. telle que
est une v.a.r. telle que ![]() et, pour tout
et, pour tout ![]() ,
, ![]() .
.
![]() admet une espérance? Si oui, calculer
admet une espérance? Si oui, calculer ![]() ;
;
Réponse : ![]() , donc
, donc ![]() , et la série de terme général
, et la série de terme général ![]()
Méthode 5 : Comment utiliser les inégalités dans les études d’espérance?
![]() On peut prouver l’existence d’une espérance par domination: si
On peut prouver l’existence d’une espérance par domination: si ![]() et
et ![]() sont deux v.a.r. discrètes telles que
sont deux v.a.r. discrètes telles que ![]() p.s., et si
p.s., et si ![]() admet une
admet une
espérance, alors ![]() admet une espérance et
admet une espérance et ![]() .
.
Pour des v.a.r. qui admettent une espérance, deux propriétés:
![]() Positivité de l’espérance: si
Positivité de l’espérance: si ![]() est une variable discrète positive qui admet une espérance,
est une variable discrète positive qui admet une espérance, ![]() , et si
, et si ![]() , alors
, alors
![]() p.s..
p.s..
![]() Croissance de l’espérance: si
Croissance de l’espérance: si ![]() et
et ![]() sont deux v.a.r. discrètes qui admettent des espérances et si
sont deux v.a.r. discrètes qui admettent des espérances et si ![]() p.s., alors
p.s., alors ![]()
Exemple :
![]() est une v.a.r. à valeurs dans
est une v.a.r. à valeurs dans ![]() qui admet une espérance, et
qui admet une espérance, et ![]() . Montrer que
. Montrer que ![]() admet une espérance et que
admet une espérance et que
![]() .
.
Réponse : On a: ![]() , donc
, donc ![]() existe et
existe et ![]() .
.
Méthode 6 : Comment définir une probabilité conditionnelle? une loi conditionnelle?
![]() Si
Si ![]() est un événement tel que
est un événement tel que ![]() , on peut définir la probabilité conditionnelle par
, on peut définir la probabilité conditionnelle par ![]() : pour tout événement
: pour tout événement ![]() ,
, ![]() . Alors
. Alors ![]() est une probabilité sur
est une probabilité sur ![]() .
.
![]() Si
Si ![]() est une v.a.r. sur
est une v.a.r. sur ![]() , si
, si ![]() est un événement de probabilité non nulle, la loi de
est un événement de probabilité non nulle, la loi de ![]() sachant
sachant ![]() est la loi de
est la loi de ![]() pour la probabilité
pour la probabilité ![]() . Elle est donnée par
. Elle est donnée par ![]() et les
et les ![]() pour tout
pour tout ![]() de
de ![]() .
.
Exemple :
![]() est une v.a.r. sur
est une v.a.r. sur ![]() qui suit une loi géométrique de paramètre
qui suit une loi géométrique de paramètre ![]() .
.
Méthode 7 : Qu’est-ce que l’espérance sachant ![]() ? Comment l’utiliser?
? Comment l’utiliser?
![]() Si
Si ![]() est un événement de probabilité non nulle, l’espérance de
est un événement de probabilité non nulle, l’espérance de ![]() sachant
sachant ![]() , si elle existe, est l’espérance de
, si elle existe, est l’espérance de ![]() pour la probabilité
pour la probabilité ![]() :
:
![]() , si cette série est absolument convergente.
, si cette série est absolument convergente.
![]() On l’utilise dans la formule de l’espérance totale:
On l’utilise dans la formule de l’espérance totale:
Si ![]() est un système complet d’événements,
est un système complet d’événements, ![]() admet une espérance si et seulement si
admet une espérance si et seulement si
![Rendered by QuickLaTeX.com \displaystyle \sum_{\stackrel{(x_{i},k)\in X(\Omega)\times \mathbb{N}}{\mathbb{P}(A_{k})\neq 0}}|x_{i}|\mathbb{P}_{A_{k}}([X=x_{i}])\mathbb{P}(A_{k})](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cadeefd101ab5b286c16a203e7b1aae1_l3.png) converge;
converge;
alors pour tout ![]() tel que
tel que ![]() ,
, ![]() existe et
existe et
![]() .
.
Exemple : Les ![]() forment un système complet d’événements tels que, pour tout
forment un système complet d’événements tels que, pour tout ![]() ,
, ![]() . La loi de
. La loi de ![]() sachant
sachant ![]() est uniforme
est uniforme
sur ![]() . Montrer que
. Montrer que ![]() admet une espérance et la calculer.
admet une espérance et la calculer.
3. Compléments sur les intégrales généralisées
Méthode 8 : Comment définir le reste d’une intégrale convergente? Comment l’utiliser?
![]() Si
Si ![]() est continue sur
est continue sur ![]() (ou
(ou ![]() ), et si
), et si ![]() (ou
(ou ![]() ) converge,
) converge,
on décomposera souvent l’intégrale en ![]() pour
pour
![]() (ou
(ou ![]() , pour
, pour ![]() ).
).
![]() est l’intégrale de la fonction
est l’intégrale de la fonction ![]() continue sur
continue sur ![]() , le second terme,
, le second terme, ![]()
(ou ![]() ), est le reste.
), est le reste.
Quand ![]() (ou quand
(ou quand ![]() ),
), ![]()
(ou ![]() ), donc le reste tend vers 0 :
), donc le reste tend vers 0 :
si ![]() converge,
converge, ![]() quand
quand ![]() ;
;
si ![]() converge,
converge, ![]() quand
quand ![]() .
.
![]() Si
Si ![]() est continue sur
est continue sur ![]() (ou sur
(ou sur ![]() , et si
, et si ![]()
(ou ![]() ) converge,on écrira de même
) converge,on écrira de même
![]() pour
pour ![]()
(ou ![]() pour
pour ![]() )
)
Le reste est alors ![]() (ou
(ou ![]() ), il tend vers
), il tend vers ![]() quand
quand ![]() (ou quand
(ou quand ![]() ).
).
Exemple : Calculer ![]() .
.
Réponse :
La fonction intégrée est continue sur ![]() et
et
![]() converge.
converge.
Pour ![]() ,
, ![]() est le reste de cette intégrale, il tend vers
est le reste de cette intégrale, il tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() ,
, ![]() .
.
Méthode 9 : Comment intégrer par parties dans une intégrale généralisée?
Si ![]() où
où ![]() et
et ![]() sont de classe
sont de classe ![]() sur un intervalle
sur un intervalle ![]() , on effectue une intégration par parties sur un segment
, on effectue une intégration par parties sur un segment ![]() inclus dans
inclus dans ![]() :
:
![]() .
.
Si ![]() (ou
(ou ![]() ), on prend
), on prend ![]() , et, si on le peut, on passe à la limite dans l’égalité quand
, et, si on le peut, on passe à la limite dans l’égalité quand ![]() (ou quand
(ou quand ![]() );
);
si ![]() (ou
(ou ![]() ), on prend
), on prend ![]() , et, si on le peut, on passe à la limite dans l’égalité quand
, et, si on le peut, on passe à la limite dans l’égalité quand ![]() (ou quand
(ou quand ![]() ).
).
Exemple :
Existence et valeur de ![]() .
.
Méthode 10 : Comment effectuer un changement de variable dans une intégrale généralisée?
On utilise le théorème suivant:
Si ![]() est continue sur
est continue sur ![]() , (
, (![]() réels ou infinis), si
réels ou infinis), si ![]() (
(![]() réels ou infinis), est une bijection strictement
réels ou infinis), est une bijection strictement
monotone de classe ![]() ,
, ![]() et
et ![]() sont de même nature, et
sont de même nature, et
![]() .
.
Remarque 1: si ![]() est strictement croissante,
est strictement croissante, ![]() et
et ![]() ;
;
Si ![]() est strictement décroissante,
est strictement décroissante, ![]() et
et ![]() ; on préfère écrire pour la suite des calculs
; on préfère écrire pour la suite des calculs
![]() .
.
Remarque 2: dans une intégrale généralisée, on peut toujours effectuer un changement de variable affine: ![]() , où
, où ![]() .
.
Exemple :
Existence et valeur de ![]() .
.
Indication : On pourra effectuer le changement de variable ![]()
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
4. Compléments sur les variables aléatoires à densité
Méthode 11 : ![]() est une v.a.r. à densité sur
est une v.a.r. à densité sur ![]() . On considère une v.a.r.
. On considère une v.a.r. ![]() de la forme
de la forme ![]() .
.
Comment savoir si ![]() est à densité et trouver sa loi?
est à densité et trouver sa loi?
On cherche la fonction de répartition ![]() de
de ![]() . Si
. Si ![]() est continue sur
est continue sur ![]() et
et ![]() sur
sur ![]() privé peut-être d’un nombre fini de points,
privé peut-être d’un nombre fini de points,
![]() est à densité.
est à densité.
Une densité de ![]() est donnée par
est donnée par ![]() si
si ![]() est dérivable en
est dérivable en ![]() ,
, ![]() sinon.
sinon.
Si ![]() est nulle en dehors d’un intervalle
est nulle en dehors d’un intervalle ![]() (
(![]() et
et ![]() réels ou infinis), et strictement positive sur
réels ou infinis), et strictement positive sur ![]() , alors
, alors ![]() p.s..
p.s..
Exemple : ![]() ,
, ![]() , et
, et ![]() a pour densité
a pour densité ![]() .
. ![]() admet pour densité
admet pour densité
(i) ![]() ?
?
(ii) ![]() ?
?
(iii) ![]() ?
?
Réponse :
(i) Faux: attention au signe de ![]() ; (ii) Faux; (iii) Vrai.
; (ii) Faux; (iii) Vrai.
Méthode 12 : Si ![]() est une v.a.r. à densité et si
est une v.a.r. à densité et si ![]() , comment étudier l’espérance de
, comment étudier l’espérance de ![]() ?
?
Si ![]() p.s. (
p.s. (![]() réels ou infinis), et si
réels ou infinis), et si ![]() est continue sur
est continue sur ![]() sauf peut-être en un nombre fini de points,
sauf peut-être en un nombre fini de points, ![]() admet une espérance si et seulement si
admet une espérance si et seulement si ![]() converge, et si c’est le cas,
converge, et si c’est le cas, ![]() .
.
Méthode 13 : Quelles propriétés de l’espérance peut-on utiliser pour les v.a.r. à densité?
Les propriétés suivantes sont valables pour des v.a.r. ![]() à densité:
à densité:
![]() linéarité de l’espérance: si
linéarité de l’espérance: si ![]() et
et ![]() admettent une espérance, si
admettent une espérance, si ![]() sont des réels,
sont des réels, ![]() admet une espérance et
admet une espérance et
![]() ;
;
![]() positivité de l’espérance: si
positivité de l’espérance: si ![]() est à valeurs positives et admet une espérance,
est à valeurs positives et admet une espérance, ![]() ;
;
![]() croissance de l’espérance: si
croissance de l’espérance: si ![]() p.s., et si
p.s., et si ![]() et
et ![]() admettent des espérances, alors
admettent des espérances, alors ![]() .
.
Exemple : ![]() suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre ![]() ,
, ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() .
.
L’espérance de ![]() est :
est :
(i) ![]()
(ii) ![]()
Réponse : La (ii) est vraie : ![]() et
et ![]() .
.
Méthode 14 : Comment définir le moment d’ordre ![]() ,
, ![]() , d’une v.a.r. à densité? Comment l’utiliser?
, d’une v.a.r. à densité? Comment l’utiliser?
![]() Le moment d’ordre
Le moment d’ordre ![]() de
de ![]() est l’espérance de
est l’espérance de ![]() , quand elle existe.
, quand elle existe.
![]() Si
Si ![]() est à densité et admet un moment d’ordre
est à densité et admet un moment d’ordre ![]() ,
, ![]() ,
, ![]() admet un moment d’ordre
admet un moment d’ordre ![]() pour tout entier
pour tout entier ![]() tel que
tel que ![]() .
.
Exemple : ![]() admet pour densité
admet pour densité ![]() , où
, où ![]() si
si ![]() ,
, ![]() sinon.
sinon.
![]() admet :
admet :
(i) un moment d’ordre 4 ?
(ii) aucun moment d’ordre ![]() ,
, ![]() ?
?
(iii) des moments d’ordre ![]() et
et ![]() ?
?
Réponse :
(i) Faux: ![]() diverge.
diverge.
(ii) Vrai: pour ![]() ,
, ![]() diverge.
diverge.
Méthode 15 : Comment calculer la variance ou l’écart-type d’une v.a.r. à densité ![]() ? Quelles en sont les propriétés?
? Quelles en sont les propriétés?
![]()
![]() admet une variance si et seulement si elle admet un moment d’ordre
admet une variance si et seulement si elle admet un moment d’ordre ![]() . Alors
. Alors ![]() admet une espérance et
admet une espérance et
![]() .
.
![]() Si
Si ![]() est à densité et admet une variance,
est à densité et admet une variance,
(i) ![]()
(ii) si ![]() et
et ![]() sont réels,
sont réels, ![]() admet une variance et
admet une variance et ![]() .
.
![]() Si
Si ![]() admet une variance, l’écart-type de
admet une variance, l’écart-type de ![]() est
est ![]() .
.
![]() Si
Si ![]() est à densité et admet une variance, la variable centrée réduite associée à
est à densité et admet une variance, la variable centrée réduite associée à ![]() est
est ![]() .
.
5. Loi  et loi normale
et loi normale
Méthode 16 : Qu’est-ce que la fonction ![]() ? la loi
? la loi ![]() ?
?
![]() La fonction
La fonction ![]() est définie par:
est définie par: ![]() ,
, ![]() .
.
Elle vérifie la relation: ![]()
![]() , et donc:
, et donc: ![]()
![]() .
.
![]() Une v.a.r.
Une v.a.r. ![]() suit la loi
suit la loi ![]() si elle admet pour densité
si elle admet pour densité ![]() :
: ![]() si
si ![]() ,
, ![]() sinon.
sinon.
Si ![]() suit la loi
suit la loi ![]() ,
, ![]() admet une espérance et une variance:
admet une espérance et une variance: ![]() ,
, ![]() .
.
Exemple : ![]() suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre ![]() ,
, ![]() .
.
Quelle loi suit ![]() ?
?
Réponse : ![]()
Allez plus loin, et prenez dès à présent de l’avance sur le programme de maths en ECS2 :

