Chapitres Maths en ECS2
Corrigés : Calcul différentiel en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Corrigés classiques – Calcul différentiel en ECS2
Exercice 1 :
![]() est une fonction de classe
est une fonction de classe ![]() sur
sur ![]() , à valeurs dans
, à valeurs dans ![]() .
.
Question 1 :
En utilisant la définition des dérivées partielles, ![]() . Comme pour tout
. Comme pour tout ![]() de
de ![]() ,
,
![]() ,
, ![]() .
.
Question 2 :
Si pour tout ![]() de
de ![]() ,
, ![]() , pour tout
, pour tout ![]() réel, la fonction
réel, la fonction ![]() a une dérivée nulle en
a une dérivée nulle en
tout point ![]() de
de ![]() , donc la fonction
, donc la fonction ![]() est constante sur
est constante sur ![]() ; cette fonction prend la valeur
; cette fonction prend la valeur ![]() quand
quand ![]() , donc c’est la
, donc c’est la
fonction nulle. Donc pour tous ![]() et
et ![]() réels
réels ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 :
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
On suppose que, pour ![]() , la ligne de niveau
, la ligne de niveau ![]() de
de ![]() , notée
, notée ![]() , a pour équation
, a pour équation ![]() , où
, où ![]() est une fonction de classe
est une fonction de classe ![]() sur
sur
![]() à valeurs réelles.
à valeurs réelles.
On pose, pour ![]() réel,
réel, ![]() et
et ![]() .
.
Question 1 :
Le point ![]() appartient à
appartient à ![]() , donc
, donc ![]() , donc
, donc ![]() ; la fonction
; la fonction ![]() est constante, donc sa dérivée est nulle:
est constante, donc sa dérivée est nulle: ![]()
pour tout de ![]() .
.
Les fonctions ![]() et
et ![]() sont
sont ![]() sur
sur ![]() , et
, et ![]() est
est ![]() sur
sur ![]() , donc
, donc ![]() est
est ![]() sur
sur ![]() et pour tout
et pour tout ![]() réel,
réel,
![]() .
.
On en déduit ![]() .
.
Question 2 :
L’équation de ![]() est
est ![]() .
.
Question 3 :
La droite ![]() est dirigée par le vecteur
est dirigée par le vecteur ![]() de coordonnées
de coordonnées ![]() , et on a:
, et on a:
![]() .
.
Donc ![]() et
et ![]() sont orthogonaux, donc
sont orthogonaux, donc ![]() est orthogonal à
est orthogonal à ![]() .
.
Exercice 3 :
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Question 1 :
Pour tout ![]() réel et tout
réel et tout ![]() de
de ![]() ,
, ![]() appartient à
appartient à ![]() , donc
, donc ![]() , donc
, donc
![]() , c’est-à-dire
, c’est-à-dire ![]() .
.
Pour tout ![]() de
de ![]() , la fonction
, la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() et de dérivée nulle, donc cette fonction est constante sur
et de dérivée nulle, donc cette fonction est constante sur ![]() ;
;
en particulier, elle prend la même valeur en ![]() et en
et en ![]() , donc
, donc ![]() .
.
Cette égalité est valable pour tout ![]() de
de ![]() , donc la fonction
, donc la fonction ![]() est bien constante sur
est bien constante sur ![]() .
.
Question 2 :
Si ![]() , on a par hypothèse pour tout
, on a par hypothèse pour tout ![]() de
de ![]() et tout
et tout ![]() de
de ![]() ,
, ![]() .
.
On pose pour ![]() ,
, 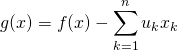 . Alors la fonction
. Alors la fonction ![]() est
est ![]() sur
sur
![]() et pour
et pour ![]() ,
, ![]() .
.
Donc pour tout ![]() de
de ![]() ,
, ![]() , donc d’après 1),
, donc d’après 1), ![]() est constante sur
est constante sur ![]() ; pour tout
; pour tout ![]() de
de ![]() ,
, ![]() ,
,
donc 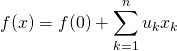 :
: ![]() est bien affine.
est bien affine.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 4 :
Pour tout ![]() de
de ![]() , on définit la fonction
, on définit la fonction ![]() qui à tout réel
qui à tout réel ![]() associe
associe ![]() . Quelque soit
. Quelque soit ![]() , la fonction
, la fonction ![]() est
est
![]() sur
sur ![]() et pour
et pour ![]() ,
, ![]() .
.
Par hypothèse, pour tout ![]() de
de ![]() et tout
et tout ![]() ,
, ![]() , donc
, donc ![]() .
.
Donc pour tout ![]() de
de ![]() et tout
et tout ![]() ,
, 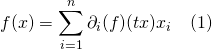 .
.
Quand ![]() , comme
, comme ![]() ,
, ![]() . Comme
. Comme ![]() est
est ![]() sur
sur ![]() , les dérivées partielles
, les dérivées partielles ![]() ,
,
![]() , sont continues sur
, sont continues sur ![]() ,
,
donc quand ![]() , pour
, pour ![]() ,
, ![]() .
.
En passant à la limite dans l’égalité ![]() quand
quand ![]() , on obtient:
, on obtient: 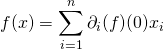 .
.
L’application ![]() est donc linéaire.
est donc linéaire.
Profitez des autres cours en ligne de maths pour les ECS2 pour réviser tous les chapitres de maths fondamentaux de la 2eme année de prépa HEC, comme :

