Chapitres Maths en ECS2
Corrigés : Réduction des endomorphismes en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Corrigés – Valeurs propres, vecteurs propres, famille libre
Dans ce chapitre, ![]() est un espace vectoriel de dimension
est un espace vectoriel de dimension ![]() ,
, ![]() , sur
, sur ![]() , (
, (![]() ou
ou ![]() ),
),
![]() est une base de
est une base de ![]() ,
, ![]() est un endomorphisme de
est un endomorphisme de ![]() ,
, ![]() est la matrice dans la base
est la matrice dans la base ![]() de
de ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 1 : valeurs propres et vecteurs propres
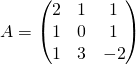 et
et 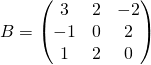 .
.
Question 1 :
Pour 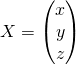 , on a:
, on a:
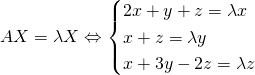
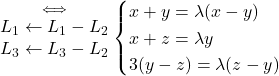 .
.
![]()
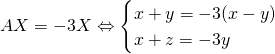
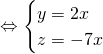
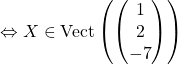 .
.
![]() Pour
Pour ![]() :
: 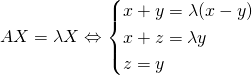
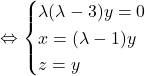 .
.
Si ![]() ,
, 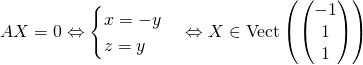
Si ![]() ,
, 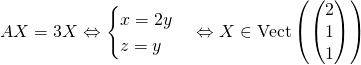
Question 2 :
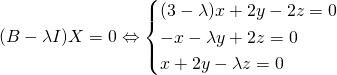
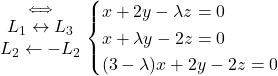
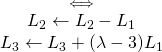
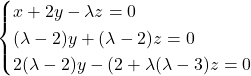
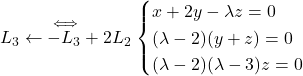 .
.
Pour ![]() :
: ![]()
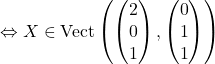
Pour ![]() :
: 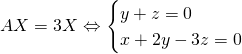
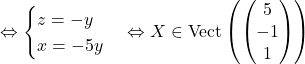 .
.
Exercice 2 : Valeurs propres et sous-espaces propres
Si ![]() , alors
, alors ![]() .
.
Les valeurs propres de ![]() sont
sont ![]() , et les sous-espaces propres associés
, et les sous-espaces propres associés ![]() ,
, ![]() ,
, ![]() .
.
Exercice 3 : Valeurs propres et sous-espaces propres
![]() est une matrice de
est une matrice de ![]() .
.
Question 1 :
![]() est valeur propre de
est valeur propre de ![]() si et seulement si
si et seulement si ![]() n’est pas inversible. Or une matrice et sa transposée sont simultanément inversibles ou non inversibles.
n’est pas inversible. Or une matrice et sa transposée sont simultanément inversibles ou non inversibles.
La transposée de ![]() est
est ![]() , donc si
, donc si ![]() est valeur propre d’une de ces deux matrices, elle est valeur propre de l’autre.
est valeur propre d’une de ces deux matrices, elle est valeur propre de l’autre.
Question 2 :
Si ![]() est une valeur propre non nulle de
est une valeur propre non nulle de ![]() , il existe
, il existe ![]() ,
, ![]() tel que
tel que ![]() . Alors
. Alors ![]() .
.
Si on avait ![]() , on aurait
, on aurait ![]() , donc
, donc ![]() , ce qui est impossible car
, ce qui est impossible car ![]() et
et ![]() . Donc
. Donc ![]() , donc
, donc ![]() est vecteur propre de
est vecteur propre de ![]() attaché à la valeur propre
attaché à la valeur propre ![]() .
.
Si ![]() est valeur propre de
est valeur propre de ![]() ,
, ![]() n’est pas inversible. Si
n’est pas inversible. Si ![]() etait inversible, alors
etait inversible, alors ![]() serait inversible: pour
serait inversible: pour ![]() ,
, ![]() entraînerait
entraînerait ![]() donc
donc ![]() . Alors, comme
. Alors, comme ![]() ,
, ![]() aussi serait inversible. Donc
aussi serait inversible. Donc ![]() serait inversible, ce qui est faux. Donc
serait inversible, ce qui est faux. Donc ![]() n’est pas inversible, donc
n’est pas inversible, donc ![]() est valeur propre de
est valeur propre de ![]() .
.
Les valeurs propres de ![]() sont donc valeurs propres de
sont donc valeurs propres de ![]() , et inversement.
, et inversement.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 4 : Familles libres et suites
![]() est une matrice à
est une matrice à ![]() lignes et
lignes et ![]() colonnes qui admet
colonnes qui admet ![]() valeurs propres distinctes
valeurs propres distinctes ![]() , donc
, donc ![]() est diagonalisable: il existe une matrice
est diagonalisable: il existe une matrice ![]() inversible de
inversible de ![]() telle que:
telle que: ![]() où
où ![]() .
.
Si 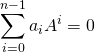 , en multipliant à gauche par
, en multipliant à gauche par ![]() et à droite par
et à droite par ![]() ,
, 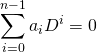 , donc, pour tout
, donc, pour tout ![]() tel que
tel que ![]() ,
, 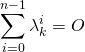 .
.
Le polynôme 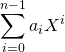 est de degré au plus
est de degré au plus ![]() et admet au moins
et admet au moins ![]() racines distinctes
racines distinctes ![]() , donc c’est le polynôme nul. Donc tous les
, donc c’est le polynôme nul. Donc tous les ![]() sont nuls.
sont nuls.
Donc la famille ![]() est libre.
est libre.
Les chapitres de maths suivants, sont également essentiels pour réussir en ECS2, révisez-les dès maintenant :

