Chapitres Maths en ECS2

Corrigés : Compléments sur les variables aléatoires réelles en ECS2

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices Corrigés

Cours en ligne de Maths en ECS2

Corrigés – Calcul de l’espérance, loi de Poisson

Exercice 1 : Boules et limite de l’espérance

$N$ boules ( $N\geq 2$ ) sont réparties dans $2$ urnes.

L’urne

$U_{1}$ contient

$K$ boules numérorées

$1,2,\dots,K$ , l’urne

$U_{2}$ contient

$N-K$ boules numérorées

$K+1,\dots,N$ . Une épreuve consiste à choisir au hasard un numéro dans

$1,\dots,N$ , et à changer d’urne la boule portant ce numéro. Pour

$n\in \mathbb{N}^{*}$ , on désigne par

$X_{n}$ le nombre de boules qui se trouvent dans l’urne

$U_{1}$ après

$n$ épreuves. Question 1 : Sur

$[X_{n}=0]$ ,

$X_{n+1}$ prend la valeur

$1$ :

$U_{1}$ ne contenait pas de boule, la boule a donc été prise dans

$U_{2}$ et mise dans

$U_{1}$ . Sur

$[X_{n}=N]$ ,

$X_{n+1}$ prend la valeur

$N-1$ :

$U_{1}$ contenait toutes les boules, la boule a donc été prise dans

$U_{1}$ et mise dans

$U_{2}$ .

Sur

$[X_{n}=k]$ ,

$1\leq k\leq N-1$ ,

$X_{n+1}$ prend la valeur

$k-1$ avec probabilité

$k/N$ : c’est la probabilité que l’on ait tiré l’un des numéros des boules de

$U_{1}$ , et

$X_{n+1}$ prend la valeur

$k+1$ avec probabilité

$(N-k)/N$ : c’est la probabilité que l’on ait tiré l’un des

$N-k$ numéros de

$U_{2}$ . Donc

$\mathbb{P}_{[X_{n}=k]}(X_{n+1}=k-1)=k/N$ , et

$\mathbb{P}_{[X_{n}=k]}(X_{n+1}=k+1)=(N-k)/N$ . On remarque que ces relations sont aussi valables pour

$k=0$ et

$k=N$ .

Question 2 :

$X_{n+1}$ est une v.a.r. finie, donc elle admet une espérance. En utilisant la formule de l’espérance toale:

$\displaystyle \mathbb{E}(X_{n+1})=$ $\displaystyle \sum_{k=0}^{N} \mathbb{E}(X_{n+1}|[X_{n}=k])\mathbb{P}([X_{n}=k])$ .

Or $\displaystyle \mathbb{E}(X_{n+1}|[X_{n}=k])=$ $\displaystyle (k-1)\dfrac{k}{N}+(k+1)\dfrac{N-k}{N}=$ $\displaystyle \dfrac{N-2}{N}k+1$ . Donc

$\mathbb{E}(X_{n+1})=$ $\displaystyle \sum_{k=0}^{N}\left((1-\dfrac{2}{N})k\mathbb{P}([X_{n}=k])+\mathbb{P}([X_{n}=k])\right)$ $\displaystyle =(1-\dfrac{2}{N})\mathbb{E}(X_{n})+1$ .

Question 3 :

La suite $(\mathbb{E}(X_{n}))$ est arithmético-géométrique. Si $\ l=(1-\dfrac{2}{N})l+1$ , $\ l=\dfrac{N}{2}$ . On a alors:

$\mathbb{E}(X_{n+1})-\dfrac{N}{2}=(1-\dfrac{2}{N})\left(\mathbb{E}(X_{n})-\dfrac{N}{2}\right)$ , et comme $\mathbb{E}(X_{0})=K$ , on obtient:

$\mathbb{E}(X_{n})-\dfrac{N}{2}=\left(1-\dfrac{2}{N}\right)^{n} (K-\dfrac{N}{2})$ .

Si $N=2$ , $\mathbb{E}(X_{n})=1$ pour $n\geq 1$ . Si $N\geq 3$ , $0<1-\dfrac{2}{N}<1$ , donc $\left(1-\dfrac{2}{N}\right)^{n}\to 0$ quand $n\to +\infty$ , donc $\mathbb{E}(X_{n})\to \dfrac{N}{2}$ quand $n\to +\infty$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Exercice 2 : Loi et calcul de l’espérance

Une urne contient $n$ boules numérotées de $1$ à $n$ ( $n\geq 2$ ).

On effectue des tirages successifs d’une boule de l’urne, en remettant chaque fois la boule tirée dans l’urne avant le tirage suivant.

Pour $1\leq i\leq n$ , $Y_{i}$ désigne le rang du tirage où l’on voit apparaître pour la première fois $i$ numéros distincts, si cette circonstance se produit,sinon $Y_{i}$ prend la valeur $0$ .

Question 1 :

On a

$Y_{1}=1$ : le premier numéro est évidemment un nouveau numéro.

$Y_{2}(\Omega)=\{0\}\cup [2,+\infty[$ . Pour

$k\geq 2$ ,

$[Y_{2}=k]=\{(j,\dots,j,i)|\ k-1$ éléments

$j,i\neq j\}$ , donc

$\mathbb{P}([Y_{2}=k])=$

$\dfrac{n\times 1\times\dots\times 1\times (n-1)}{n\times n\times \dots\times n\times n}=$

$\dfrac{n-1}{n^{k-1}}$ . Et

$\mathbb{P}([Y_{2}=0])=$

$1-\displaystyle \sum_{k=2}^{+\infty}\mathbb{P}([Y_{2}=k])=$

$\displaystyle 1-\dfrac{n-1}{n}\sum_{k=2}^{+\infty} \left(\dfrac{1}{n}\right)^{k-2}=$

$1-\dfrac{n-1}{n}\dfrac{1}{1-\dfrac{1}{n}}=0$ .

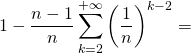
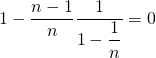Question 2 :

$Y_{2}-Y_{1}=Y_{2}-1$ , donc

$(Y_{2}-Y_{1})(\Omega)=[1,+\infty[$ p.s., et pour

$k\in \mathbb{N}^{*}$ ,

$\mathbb{P}([Y_{2}-Y_{1}=k])=\mathbb{P}([Y_{2}=k+1])=$

$\left(\dfrac{1}{n}\right)^{k-1}\left(1-\left(\dfrac{1}{n}\right)\right)$ , donc

$Y_{2}-Y_{1}$ suit une loi géométrique de paramètre

$1-(1/n)$ . Question 3 : (i) Pour

$1\leq i\leq n-1$ ,

$Y_{i+1}-Y_{i}$ prend ses valeurs dans

$[1, +\infty[$ : il faut au moins un tirage supplémentaire pour voir apparaître un nouveau numéro, et on peut aussi tirer toujours des numéros déjà obtenus. Une éventualité de

$[Y_{i+1}-Y_{i}=j]\cap[[Y_{i}=k]$ , (

$j\geq 1$ ,

$i\leq k$ ), est de la forme (une éventualité de

$[Y_{i}=k]$ , une suite de j-1 numéros faisant partie des i numéros déjà obtenus, un nouveau numéro) Donc :

$\mathbb{P}([Y_{i+1}-Y_{i}=j])\cap [Y_{i}=k])=$

$\mathbb{P}([Y_{i}=k])\left(\dfrac{i}{n}\right)^{j-1} \dfrac{n-i}{n}$ , donc

$\mathbb{P}_{[Y_{i}=k]}([Y_{i+1}-Y_{i}=j])=$

$\left(\dfrac{i}{n}\right)^{j-1}\dfrac{n-i}{n}$ . Donc la loi de

$Y_{i+1}-Y_{i}$ sachant

$[Y_{i}=k]$ est géométrique de paramètre

$1-(i/n)$ . (ii) En utilisant la formule des probabilités totales avec le système quasi-complet d’événements

$\displaystyle ([Y_{i}=k])_{k\geq i}$ , on obtient:

$\mathbb{P}([Y_{i+1}-Y_{i}=j])=$

$\displaystyle \sum_{k=i}^{+\infty} \left(\dfrac{i}{n}\right)^{j-1}\dfrac{n-i}{n} \mathbb{P}([Y_{i}=k])=$

$\displaystyle \left(\dfrac{i}{n}\right)^{j-1}\dfrac{n-i}{n} \sum_{k=i}^{+\infty} \mathbb{P}([Y_{i}=k])=$

$\left(\dfrac{i}{n}\right)^{j-1}\dfrac{n-i}{n}$ . Donc

$Y_{i+1}-Y_{i}$ suit une loi géométrique de paramètre

$1-(i/n)$ .

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Exercice 3 : Loi de Poisson de paramètre $\lambda$

$A$ est une matrice de $\mathcal{M}_{n}(\mathbb{K})$ .

Le nombre $N$ de clients fréquentant un centre commercial est une v.a.r. qui suit une loi de Poisson de paramètre $\lambda$ , $\lambda>0$ .

La probabilité qu’un client y effectue un achat est $p$ , $p\in ]0,1[$ . $X$ désigne le nombre de clients qui effectuent un achat; on admet que $X$ est une v.a.r..

Question 1 :

Chaque client peut effectuer un achat (succès) ou non (échec). Les décisions des clients sont indépendantes les unes des autres, et la probabilité de succès est $p$ .

Sur $[N=n]$ , $X$ prend pour valeur le nombre de succès en $n$ épreuves.

Donc la loi de $X$ sachant $[N=n]$ est binômiale de paramètre $(n,p)$ , et donc l’espérance de $X$ sachant $[N=n]$ est $np$ .

Question 2 :

$X$ est à valeurs positives: $X(\Omega)=\mathbb{N}$ . Si les sommes infinies écrites convergent, on a:

$\mathbb{E}(X)=$ $\displaystyle \sum_{n=0}^{+\infty}\mathbb{E}(X|\ [N=n])\mathbb{P}([N=n])=$ $\displaystyle pe^{-\lambda}\sum_{n=0}^{+\infty}n\dfrac{\lambda^{n}}{n!}=$ $\displaystyle p\lambda e^{-\lambda}\sum_{n=1}^{+\infty}\dfrac{\lambda^{n-1}}{(n-1)!}$ .

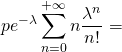
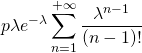Cette dernière série converge et a pour somme $e^{\lambda}$ . Donc $X$ admet une espérance et $\mathbb{E}(X)=p\lambda$ .

Question 3 :

Pour $k\in \mathbb{N}$ , $[X=k]=\displaystyle \bigcup_{n=0}^{+\infty} \left([X=k]\cap[N=n]\right)$ .

Les événements de l’union sont deux à deux disjoints, et vides si

$n<k$ : il ne peut pas y avoir plus d’acheteurs que de clients. Donc: $\mathbb{P}([X=k])=$ $\displaystyle \sum_{n=k}^{+\infty} \mathbb{P}([N=n])\mathbb{P}_{[N=n]}([X=k])=$ $\displaystyle \sum_{n=k}^{+\infty} e^{-\lambda}\dfrac{\lambda^{n}}{n!}{n\choose k}p^{k}(1-p)^{n-k}=$ $e^{-\lambda}\dfrac{(\lambda p)^{k}}{k!}\displaystyle \sum_{n=k}^{+\infty} \dfrac{(\lambda (1-p))^{n-k}}{(n-k)!}$ .

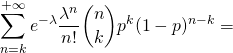
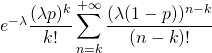Cette dernière somme vaut $e^{\lambda (1-p)}$ , donc $\mathbb{P}([X=k])=e^{-\lambda p}\dfrac{(\lambda p)^{k}}{k!}$ , donc $X$ suit une loi de Poisson de paramètre $\lambda p$ .

Des progrès en maths ne seront visibles que si les révisons et les entraînements sont réguliers, pour cela aidez-vous de nos cours en ligne d’ECS2 en maths :

Corrigés : Compléments sur les variables aléatoires réelles en ECS2

Corrigés – Calcul de l’espérance, loi de Poisson

Exercice 1 : Boules et limite de l’espérance

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Exercice 2 : Loi et calcul de l’espérance

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Exercice 3 : Loi de Poisson de paramètre $\lambda$

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales