Chapitres Maths en ECS2
Cours : Couples de variables aléatoires discrètes
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Lois, Indépendance, Somme, Covariance
1. Loi d’un couple  de v.a.r. discrètes
de v.a.r. discrètes
Méthode 1 : Si ![]() et
et ![]() sont deux variables aléatoires discrètes définies sur un même espace probabilisé
sont deux variables aléatoires discrètes définies sur un même espace probabilisé ![]() , qu’est-ce que la tribu liée au couple
, qu’est-ce que la tribu liée au couple ![]() ? Quels liens y a-t-il avec les tribus liées à
? Quels liens y a-t-il avec les tribus liées à ![]() et à
et à ![]() ?
?
![]() La tribu liée au couple
La tribu liée au couple ![]() , notée
, notée ![]() , est la plus petite tribu sur
, est la plus petite tribu sur ![]() contenant les
contenant les ![]() ,
,
![]() , où
, où ![]() est l’ensemble des valeurs prises par le couple
est l’ensemble des valeurs prises par le couple ![]() .
.
![]() Les
Les ![]() ,
, ![]() , forment un système complet d’événements, donc pour tout
, forment un système complet d’événements, donc pour tout ![]() de
de ![]() ,
,
![]() , donc
, donc ![]() .
.
Donc ![]() , et de même,
, et de même, ![]() .
.
En cas de lacunes en ECS2, retrouvez nos profs de maths sur notre plateforme pour vous conduire vers la réussite scolaire en maths.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Exemple :
Si ![]() et
et ![]() sont deux variables aléatoires définies sur
sont deux variables aléatoires définies sur ![]() , à valeurs dans
, à valeurs dans ![]() ,
, ![]() contient,
contient,
pour tous ![]() et
et ![]() de
de ![]() , les événements
, les événements ![]() , les
, les ![]() , les
, les ![]() .
.
Méthode 2 : Si ![]() et
et ![]() sont deux v.a.r. discrètes sur
sont deux v.a.r. discrètes sur ![]() , comment peut-on donner la loi du couple
, comment peut-on donner la loi du couple ![]() ?
?
La loi du couple ![]() est donnée par:
est donnée par:
![]() l’ensemble
l’ensemble ![]() des valeurs prises par le couple;
des valeurs prises par le couple;
![]() pour tout
pour tout ![]() de
de ![]() ,
, ![]() .
.
Les ![]() ,
,![]() , forment un système complet d’événements.
, forment un système complet d’événements.
On peut remarquer que ![]() .
.
Exemple : ![]() suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre ![]() ,
, ![]() . Trouver la loi du couple
. Trouver la loi du couple ![]() .
.
Méthode 3 : Comment reconnaître qu’une famille ![]() est la loi d’un couple
est la loi d’un couple ![]() de v.a.r. à valeurs dans
de v.a.r. à valeurs dans ![]() (c’està-dire que pour tous
(c’està-dire que pour tous ![]() de
de ![]() ,
, ![]() )?
)?
C’est le cas si et seulement si pour tout ![]() de
de ![]()
![]() , et
, et ![]() , ce qui traduit
, ce qui traduit
que les ![]() ,
, ![]() forment un système complet d’événements.
forment un système complet d’événements.
Exemple : La famille ![]() est la loi d’un couple de v.a.r. discrètes pour
est la loi d’un couple de v.a.r. discrètes pour ![]() = …
= …
(i) ![]() ?
?
(ii) ![]() ?
?
(iii) ![]() ?
?
Réponse : (ii)
Méthode 4 : Comment retrouver les lois des v.a.r. discrètes ![]() et
et ![]() quand on connait la loi du couple
quand on connait la loi du couple ![]() ?
?
![]() En utilisant la formule des probabilités totales avec les systèmes complets d’événements
En utilisant la formule des probabilités totales avec les systèmes complets d’événements ![]() et
et ![]() :
:
![]()
et
![]() .
.
![]() Si
Si ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() , si pour
, si pour ![]() ,
, ![]() est placée dans la i-ème ligne et la j-ème colonne d’un tableau,
est placée dans la i-ème ligne et la j-ème colonne d’un tableau, ![]() est la somme des éléments de la i-ème ligne du tableau,
est la somme des éléments de la i-ème ligne du tableau, ![]() est la somme des éléments de la j-ème colonne.
est la somme des éléments de la j-ème colonne.
Les lois de ![]() et
et ![]() sont appelées lois marginales du couple: on inscrit leurs valeurs dans les marges du tableau.
sont appelées lois marginales du couple: on inscrit leurs valeurs dans les marges du tableau.
Exemple : Pour ![]() ,
, ![]() . On admet que la famille
. On admet que la famille ![]() est la loi d’un couple
est la loi d’un couple ![]() de v.a.r. discrètes. Alors :
de v.a.r. discrètes. Alors :
(i) ![]() suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre ![]() et
et ![]() une loi de Poisson de paramètre
une loi de Poisson de paramètre ![]() ?
?
(ii) ![]() et
et ![]() suivent une loi de Poisson de paramètre
suivent une loi de Poisson de paramètre ![]() ?
?
(iii) ![]() et
et ![]() suivent une loi de Poisson de paramètre
suivent une loi de Poisson de paramètre ![]() ?
?
Réponse : (iii)
2. Indépendance
Méthode 5 : Comment montrer que deux v.a.r. discrètes ![]() et
et ![]() sont indépendantes ?
sont indépendantes ?
![]() Les v.a.r. discrètes
Les v.a.r. discrètes ![]() et
et ![]() sont indépendantes si et seulement si : pour tout
sont indépendantes si et seulement si : pour tout ![]() de
de ![]() et tout
et tout ![]() de
de ![]() ,
,
![]()
![]()
Exemple : ![]() et
et ![]() sont deux v.a.r. sur
sont deux v.a.r. sur ![]() qui suivent des lois de Bernouilli de paramètres
qui suivent des lois de Bernouilli de paramètres ![]() et
et ![]() .
. ![]() et
et ![]() sont indépendantes si ,et seulement si …(i)
sont indépendantes si ,et seulement si …(i) ![]() suit une loi de
suit une loi de ![]()
(ii) ![]() et
et ![]() sont indépendants
sont indépendants
(iii) ![]() et
et ![]() sont indépendants
sont indépendants
Réponse : Les 3 réponses sont correctes !
(i) ![]() , donc si
, donc si ![]() et
et ![]() sont indépendantes,
sont indépendantes, ![]() prend la valeur
prend la valeur ![]() avec probabilité
avec probabilité ![]() , et sinon prend la valeur
, et sinon prend la valeur ![]() ; réciproquement, si
; réciproquement, si ![]() suit une loi de Bernouilli de paramètre
suit une loi de Bernouilli de paramètre ![]() ,
, ![]() et
et ![]() sont indépendants, donc le complémentaire de
sont indépendants, donc le complémentaire de ![]() ,
, ![]() , et
, et ![]() aussi, donc aussi par le même argument
aussi, donc aussi par le même argument ![]() et
et ![]() , donc enfin
, donc enfin ![]() et
et ![]() ; donc
; donc ![]() et
et ![]() sont indépendantes.
sont indépendantes.
(ii) Si deux événements sont indépendants, on peut remplacer l’un des deux, ou les deux, par leur complémentaire, on obtient encore des événements indépendants.
(iii) Si deux événements sont indépendants, on peut remplacer l’un des deux, ou les deux, par leur complémentaire, on obtient encore des événements indépendants.
Méthode 6 : Comment exploiter l’indépendance de deux v.a.r. discrètes sur ![]() ?
?
Si ![]() et
et ![]() sont indépendantes, toute union d’événements
sont indépendantes, toute union d’événements ![]() ,
,![]() , est indépendante de toute union d’événements
, est indépendante de toute union d’événements ![]() ,
, ![]() .
.
En particulier, pour tous ![]() et
et ![]() de
de ![]() ,
, ![]() et
et ![]() sont indépendants.
sont indépendants.
Ex: ![]() et
et ![]() sont deux v.a.r. sur
sont deux v.a.r. sur ![]() à valeurs dans
à valeurs dans ![]() .
.
On pose, pour tout ![]() de
de ![]() ,
, ![]() et
et ![]() .
.
Calculer, pour tout ![]() de
de ![]() ,
, ![]() et
et ![]() .
.
Réponse :
![]()
et ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
3. Somme de deux v.a.r. discrètes indépendantes
Méthode 7 : Comment trouver la loi de ![]() quand
quand ![]() et
et ![]() sont deux v.a.r. discrètes indépendantes sur
sont deux v.a.r. discrètes indépendantes sur ![]() ?
?
Qu’est-ce que le produit de convolution discret ?
![]() Si
Si ![]() ,
, ![]() , et pour tout
, et pour tout ![]() de
de ![]()
![]()
![]()
![]() Si
Si ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() , on note, pour tous
, on note, pour tous ![]() de
de ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Alors pour tout ![]() de
de ![]() ,
, 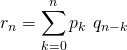 .
.
On écrit ![]() :
: ![]() est le produit de convolution,
est le produit de convolution, ![]() est la convolée de
est la convolée de ![]() et
et ![]() . On a :
. On a : ![]() .
.
Si dans un tableau rectangulaire, ![]() est placé à l’intersection de la
est placé à l’intersection de la ![]() ligne et de la
ligne et de la ![]() colonne,
colonne, ![]() est la somme des éléments de la diagonale numéro
est la somme des éléments de la diagonale numéro ![]() du tableau (la diagonale numéro
du tableau (la diagonale numéro ![]() a
a ![]() élément:
élément: ![]() , la diagonale numéro
, la diagonale numéro ![]() en a
en a ![]() :
: ![]() et
et ![]() , etc…).
, etc…).
Exemple : ![]() et
et ![]() sont deux v.a.r. indépendantes,sur un même espace probabilisé qui suivent des lois de Bernouilli de paramètres
sont deux v.a.r. indépendantes,sur un même espace probabilisé qui suivent des lois de Bernouilli de paramètres ![]() et
et ![]() . Alors :
. Alors :
(i) ![]() suit une loi de Bernouilli de paramètre
suit une loi de Bernouilli de paramètre ![]() ?
?
(ii) ![]() ne suit pas une loi de Bernouilli mais
ne suit pas une loi de Bernouilli mais ![]() ?
?
(iii) ![]() ne suit pas une loi de Bernouilli mais
ne suit pas une loi de Bernouilli mais ![]() ?
?
Réponse :
(i) Non : ![]() .
.
(ii) Oui : ![]() et
et ![]() ,
, ![]() .
.
(iii) Oui et Non : ![]()
Méthode 8 : Qu’est-ce que la stabilité des lois binomiales et de Poisson?
![]() si
si ![]() et
et ![]() sont deux v.a.r. définies sur le même espace probabilisé, si
sont deux v.a.r. définies sur le même espace probabilisé, si ![]() suit une loi
suit une loi ![]() et
et ![]() une loi
une loi ![]() et si
et si ![]() et
et ![]() sont indépendantes,
sont indépendantes, ![]() suit une loi
suit une loi ![]() .
.
Interprétation : On effectue des épreuves successives indépendantes où la probabilité de succès est ![]() .
.
![]() compte le nombre de succès obtenus pendant les
compte le nombre de succès obtenus pendant les ![]() premières épreuves,
premières épreuves, ![]() le nombre de succès obtenus pendant les
le nombre de succès obtenus pendant les ![]() épreuves suivantes.
épreuves suivantes.
Alors ![]() et
et ![]() sont indépendantes, et
sont indépendantes, et ![]() compte le nombre de succès au cours des
compte le nombre de succès au cours des ![]() premières épreuves.
premières épreuves.
![]() Si
Si ![]() et
et ![]() sont deux v.a.r. définies sur le même espace probabilisé, indépendantes, suivant des lois de Poisson de paramètres
sont deux v.a.r. définies sur le même espace probabilisé, indépendantes, suivant des lois de Poisson de paramètres ![]() et
et ![]() , alors
, alors ![]() suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre ![]() .
.
Exemple : Si ![]() et
et ![]() sont définies sur le même espace probabilisé, indépendantes, et suivent des lois géométriques,
sont définies sur le même espace probabilisé, indépendantes, et suivent des lois géométriques, ![]() suit-elle une loi géométrique ?
suit-elle une loi géométrique ?
Réponse : Non !
4. Etude de v.a.r. de la forme 
Méthode 9 : Comment trouver la loi d’une v.a.r de la forme ![]() où
où ![]() est une application définie sur
est une application définie sur ![]() (au moins) à valeurs réelles et
(au moins) à valeurs réelles et ![]() un couple de v.a.r. discrètes définies sur
un couple de v.a.r. discrètes définies sur ![]() ?
?
En notant ![]() , on a:
, on a: ![]() .
.
Pour tout ![]() de
de ![]() ,
, ![]() : on voit que les
: on voit que les ![]() appartiennent à la tribu liée au couple
appartiennent à la tribu liée au couple ![]() , c’est-à-dire que
, c’est-à-dire que ![]() .
.
On a alors:
![]()
![]()
Méthode 10 : Comment étudier l’espérance d’une v.a.r. de la forme ![]() , où
, où ![]() est un couple de v.a.r. discrètes définies sur
est un couple de v.a.r. discrètes définies sur ![]() à l’aide du théorème de transfert ?
à l’aide du théorème de transfert ?
Le théorème de transfert permet d’étudier l’espérance de ![]() sans en calculer la loi, à partir de la loi du couple
sans en calculer la loi, à partir de la loi du couple ![]() :
:
![]() admet une espérance si et seulement la série
admet une espérance si et seulement la série ![]() converge et alors
converge et alors
![]()
![]()
Certains calculs se font plus simplement en utilisant ![]() .
.
Par exemple si ![]() et
et ![]() sont semblables, pour tout entier naturel
sont semblables, pour tout entier naturel ![]() ,
, ![]() et
et ![]() sont semblables (ce sont deux matrices de
sont semblables (ce sont deux matrices de ![]() ): si
): si ![]() ,
, ![]() .
.
Exemple : On sait que 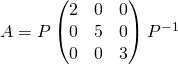 . Calculer
. Calculer ![]() .
.
Réponse : 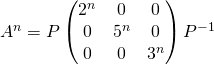 .
.
5. Espérance, covariance, variance, corrélation linéaire
Méthode 11 : Que peut-on dire de l’espérance d’une combinaison linéaire ou d’un produit de v.a.r. discrètes sur un même espace probabilisé ?
![]() L’espérance est linéaire: si
L’espérance est linéaire: si ![]() et
et ![]() sont deux v.a.r. discrètes sur un même espace probabilisé qui admettent une espérance, si
sont deux v.a.r. discrètes sur un même espace probabilisé qui admettent une espérance, si ![]() et
et ![]() sont des réels,
sont des réels, ![]() admet une espérance et
admet une espérance et ![]() .
.
![]() Si
Si ![]() et
et ![]() sont deux v.a.r. discrètes sur un même espace probabilisé, indépendantes, qui admettent une espérance, alors
sont deux v.a.r. discrètes sur un même espace probabilisé, indépendantes, qui admettent une espérance, alors ![]() admet une espérance et
admet une espérance et ![]() .
.
En général, si ![]() et
et ![]() admettent un moment d’ordre
admettent un moment d’ordre ![]() , c’est-à-dire si
, c’est-à-dire si ![]() et
et ![]() admettent une espérance,
admettent une espérance, ![]() admet une espérance et
admet une espérance et ![]() .
.
Méthode 12 : Qu’est-ce que la covariance ? Quand existe-t-elle ? Comment la calculer ?
Si ![]() est un couple de v.a.r. discrètes définies sur un même espace probabilisé la covariance du couple
est un couple de v.a.r. discrètes définies sur un même espace probabilisé la covariance du couple ![]() , quand elle existe est définie par:
, quand elle existe est définie par:
![]()
La covariance de ![]() existe quand
existe quand ![]() admet une espérance, ce qui est réalisé si
admet une espérance, ce qui est réalisé si ![]() et
et ![]() admettent un moment d’ordre
admettent un moment d’ordre ![]() .
.
La formule de Huygens donne: ![]() .
.
Exemple : On effectue ![]() (
(![]() ) d’un dé bien équilibré.
) d’un dé bien équilibré. ![]() prend la valeur
prend la valeur ![]() si on obtient un
si on obtient un ![]() au premier lancer, et
au premier lancer, et ![]() sinon,
sinon, ![]() prend la valeur
prend la valeur ![]() si on obtient un
si on obtient un ![]() aux premier et
aux premier et ![]() lancés, la valeur
lancés, la valeur ![]() sinon.
sinon.
Que vaut la covariance de ![]() ?
?
Réponse : ![]() .
.
![]() et
et ![]() suivent des lois de Bernouilli de paramètres
suivent des lois de Bernouilli de paramètres ![]() et
et ![]() , et
, et ![]() .
.
Méthode 13 : Quelles sont les propriétés de la covariance ?
![]() La covariance est bilinéaire, symétrique, positive:
La covariance est bilinéaire, symétrique, positive:
![]()
![]() ;
;
![]() Si
Si ![]() et
et ![]() admettent une covariance, si
admettent une covariance, si ![]() et
et ![]() sont des réels,
sont des réels, ![]() admet une covariance et
admet une covariance et
![]()
![]()
![]() Si
Si ![]() existe, alors
existe, alors
![]()
![]() Si
Si ![]() et
et ![]() sont deux v.a.r.discrètes indépendantes définies sur un même espace probabilisé et si
sont deux v.a.r.discrètes indépendantes définies sur un même espace probabilisé et si ![]() admet une covariance,
admet une covariance, ![]() .
.
En particulier, si ![]() est une v.a.r. constante,
est une v.a.r. constante, ![]() ,
, ![]() .
.
Exemple : ![]() et
et ![]() sont deux v.a.r. discrètes sur
sont deux v.a.r. discrètes sur![]() qui admettent un moment d’ordre
qui admettent un moment d’ordre ![]() .
.
On pose ![]()
![]() et
et ![]() , où
, où ![]() sont des réels.
sont des réels.
Alors ![]() :
:
(i) ![]()
(ii) ![]()
(iii) ![]()
Réponse : ![]()
Méthode 14 : Qu’est-ce que la variance ? l’écart-type ? Quelles en sont les propriétés ?
![]() et
et ![]() sont deux v.a.r. discrètes définies sur un même espace probabilisé.
sont deux v.a.r. discrètes définies sur un même espace probabilisé.
![]()
![]() admet une variance si et seulement si
admet une variance si et seulement si ![]() admet une espérance, et alors:
admet une espérance, et alors: ![]() .
.
![]() La formule de Huygens donne:
La formule de Huygens donne: ![]() .
.
![]() Si
Si ![]() admet une variance, on a toujours
admet une variance, on a toujours ![]() .
.
On peut donc définir l’écart-type de ![]() , noté
, noté ![]() , par:
, par: ![]() .
.
![]() Si
Si ![]() est une v.a.r. constante,
est une v.a.r. constante, ![]() .
.
Réciproquement, si ![]() admet une variance nulle,
admet une variance nulle, ![]() est presque sûrement constante:
est presque sûrement constante: ![]() p.s..
p.s..
![]() Si
Si ![]() admet une variance, pour tous
admet une variance, pour tous ![]() et
et ![]() réels,
réels, ![]() en admet une et
en admet une et ![]() .
.
![]() Si
Si ![]() et
et ![]() admettent une variance,
admettent une variance, ![]() en admet une et
en admet une et
![]()
![]()
.
En particulier, si ![]() et
et ![]() sont indépendantes,
sont indépendantes, ![]() .
.
Exemple : ![]() et
et ![]() sont deux v.a.r. discrètes sur
sont deux v.a.r. discrètes sur ![]() , qui admettent une variance, telles que:
, qui admettent une variance, telles que:
![]()
![]() .
.
Alors ![]()
(i) ![]()
(ii) ![]()
(iii) ![]()
Réponse : (iii) ![]()
![]() et
et ![]()
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 15 : Qu’est-ce que l’inégalité de Cauchy-Schwarz ?
Si ![]() et
et ![]() sont deux v.a.r. discrètes définies sur un même espace probabilisé qui admettent un moment d’ordre
sont deux v.a.r. discrètes définies sur un même espace probabilisé qui admettent un moment d’ordre ![]() , alors
, alors
![]() .
.
Exemple : Montrer que si ![]() et
et ![]() sont deux v.a.r. discrètes sur
sont deux v.a.r. discrètes sur ![]() ,
, ![]() .
.
Méthode 16 : Qu’est-ce que le coefficient de corrélation linéaire ? Quelles en sont les propriétés ?
![]() Si
Si ![]() et
et ![]() sont deux v.a.r. définies sur
sont deux v.a.r. définies sur ![]() qui admettent une variance non nulle, le coefficient de corrélation linéaire
qui admettent une variance non nulle, le coefficient de corrélation linéaire
du couple ![]() est le réel
est le réel ![]() défini par:
défini par: ![]() .
.
![]() On a:
On a: ![]() , et:
, et: ![]() si et seulement si il existe des réels
si et seulement si il existe des réels ![]() et
et ![]() tels que
tels que ![]() p.s. et
p.s. et ![]() ,
, ![]()
si et seulement si il existe des réels ![]() et
et ![]() tels que
tels que ![]() p.s. et
p.s. et ![]() .
.
Exemple : ![]() et
et ![]() sont deux v.a.r. discrètes définies sur un même espace probabilisé qui admettent un moment d’ordre
sont deux v.a.r. discrètes définies sur un même espace probabilisé qui admettent un moment d’ordre ![]() ,
, ![]() est un réel strictement positif.
est un réel strictement positif.
Alors ![]()
(i) ![]()
(ii) ![]()
(iii) ![]()
Réponse : (iii) ![]()
![]() et
et ![]()
D’autres chapitres, exercices et exercices corrigés sont à disposition des étudiants d’ECS2 pour réviser les cours de maths :

