Cours en ligne Physique en Maths Sup
Chapitres Physique en MPSI, PCSI, MP2I, PTSI
Cours de Physique : Électricité Régime sinusoïdal forcé en Maths Sup
Exercices et corrigés Cours en ligne de physique en Maths Sup
Ce cours en ligne de physique chimie pour les classes préparatoires vous permet de travailler le cours de l’électricité en régime sinusoïdal, une partie essentielle pour comprendre les phénomènes électriques complexes. Si vous rencontrez des difficultés dans ce chapitre, n’hésitez pas à consulter nos professeurs particuliers en physique chimie. Le soutien que nous offrons ne se limite pas à la durée du cours. Nous assurons un suivi pédagogique continu par une équipe d’experts, disponible avant et après les sessions, pour répondre à toutes vos questions et vous aider dans votre compréhension.
Cours & méthodes – Maths Sup Électricité Régime sinusoïdal forcé
Plan :
A. Impédances
B. Étude de circuits en RSF
C. Étude de résonance
D. Quadripôles et filtrage
A. Impédances
1. Régime sinusoïdal forcé (RSF)
En RSF, toutes les grandeurs électriques, intensités, tensions, potentiels du circuit sont sinusoïdales, de pulsation ![]() égale à celle du générateur :
égale à celle du générateur :
![]()
Elles sont caractérisées par leur amplitude ![]() et leur phase
et leur phase ![]()
On peut alors passer en grandeurs complexes (on souligne la lettre dans ce cas)
![]()
ou ![]()
avec ![]()
amplitude complexe de la grandeur.
Démonstration de cours.
Montrer qu’en grandeurs complexes, dériver par rapport au temps revient à multiplier par ![]()
Correction :
La dérivée de ![]() est
est ![]()
Or la dérivée par rapport au temps de ![]() vaut
vaut ![]() donc
donc![]()
On en déduit ![]()
2. Loi d’Ohm généralisée.
Les lois de la résistance, de l’inductance et de la capacité s’écrivent toutes sous la même forme en grandeurs complexes
![]()
où ![]() est l’impédance complexe du dipôle.
est l’impédance complexe du dipôle.
* ![]()
* ![]()
* ![]()
L’admittance est l’inverse de l’impédance
![]()
* ![]()
* ![]()
* ![]()
TOUTES les lois établies pour la résistance, association série, association parallèle, diviseur de tension, sont valables en RSF en remplaçant les résistances par les impédances.
Démonstration de cours.
Établir les expressions des impédances des trois dipôles.
Correction :
* ![]() donc
donc ![]()
* ![]() donc
donc ![]()
soit ![]()
* ![]() donc
donc ![]()
soit ![]()
B. Étude de circuits en RSF
1. Étude en grandeurs complexes.
La méthode d’étude est la même que pour les circuits avec générateur de tension continue et seulement des résistors :
on utilise la loi du diviseur de tension et on associe les impédances pour simplifier le circuit.
Exemple.
Dans un circuit formé de l’association série d’une bobine d’inductance L et d’un condensateur de capacité C, alimenté par un générateur de tension sinusoïdal ![]() , déterminer l’intensité complexe
, déterminer l’intensité complexe ![]()
Correction :
L’association a pour impédance complexe![]()
![]()
Elle est alimentée par ![]()
On en déduit ![]()
![]()
![]()
2. Du formalisme complexe à l’équation différentielle.
Dans un circuit à mailles multiples, l’établissement de l’équation différentielle par la méthode classique, fléchage des tensions et intensités, écriture des relations pour chaque dipôle et des lois de Kirchhoff, est poussive. Si le circuit ne comporte que des résistances, bobines, condensateurs, il est beaucoup plus rapide de procéder comme suit.
* Même si l’on n’est pas en RSF, on associe les différents dipôles en calculant les impédances équivalentes, on utilise la loi du diviseur de tension, et on en déduit l’équation en grandeurs complexes (voir paragraphe précédent),.
* On utilise l’équivalence « complexe-temporelle », cette fois-ci sous sa forme réciproque : multiplier par ![]() revient à dériver.
revient à dériver.
* On en déduit l’équation différentielle vérifiée par la grandeur cherchée.
Exemple.
Un circuit comporte une bobine d’inductance ![]() en série avec l’association parallèle d’une résistance
en série avec l’association parallèle d’une résistance ![]() et d’un condensateur de capacité
et d’un condensateur de capacité ![]() . Il est alimenté par un échelon de tension qui passe de 0 à
. Il est alimenté par un échelon de tension qui passe de 0 à ![]() à
à ![]()
Quelle est l’équation différentielle vérifiée par ![]() ?
?
Correction :
Notons ![]() la tension du générateur en grandeurs complexes.
la tension du générateur en grandeurs complexes.
La tension commune aux bornes de ![]() et de
et de ![]() est obtenue en calculant son impédance équivalente et en appliquant la loi du diviseur de tension.
est obtenue en calculant son impédance équivalente et en appliquant la loi du diviseur de tension. 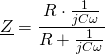
soit ![]()
et ![]()
soit ![]()
soit ![]()
En faisant le produit en croix, on en déduit ![]()
En utilisant l’équivalence complexe-temporelle, on obtient ![]()
COURS EN PREPA MATHS SUP
Les meilleurs professeurs particuliers en CPGE
POUR ACCÉLÉRER MA PROGRESSION EN PRÉPA
Avis Google France ★★★★★ 4,9 sur 5
C. Étude de résonance
1. Détermination d’une grandeur électrique en fonction de ![]()
On se place en RSF. On s’intéresse à une grandeur
![]()
car l’amplitude ![]() et la phase
et la phase ![]() dépendent a priori de la pulsation
dépendent a priori de la pulsation ![]()
Grâce au formalisme complexe, après simplification par ![]() , on obtient l’amplitude complexe
, on obtient l’amplitude complexe ![]()
et on calcule son module et son argument
![]() et
et ![]()
Exemple.
Dans un circuit série ![]() alimenté par
alimenté par ![]() déterminer l’amplitude
déterminer l’amplitude ![]() de la tension
de la tension ![]() aux bornes du condensateur.
aux bornes du condensateur.
Correction :
Par application de la loi du diviseur de tension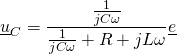
soit ![]()
En passant aux modules on obtient![]()
2. Faire une étude de résonance.
On fait simplement l’étude de la fonction mathématique ![]() , avec dérivée, tableau de variations, limites et graphe. On parle de résonance quand on obtient, pour une valeur particulière (en général non nulle) de la pulsation
, avec dérivée, tableau de variations, limites et graphe. On parle de résonance quand on obtient, pour une valeur particulière (en général non nulle) de la pulsation ![]() , un maximum de la fonction.
, un maximum de la fonction.
Exemple.
L’amplitude ![]() de la tension aux bornes d’un condensateur en série avec une résistance et une bobine (voir paragraphe précédent) a une forme qui dépend de la valeur du facteur de qualité
de la tension aux bornes d’un condensateur en série avec une résistance et une bobine (voir paragraphe précédent) a une forme qui dépend de la valeur du facteur de qualité
![]()
Dans quel cas observe-t-on une résonance ? Quel est le nom du phénomène dans ce cas ?
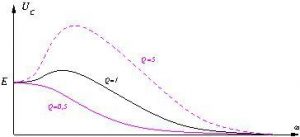
Correction :
La résonance est observée pour ![]() et pour
et pour ![]() .
.
Comme la tension aux bornes du condensateur est supérieure à la tension ![]() aux bornes du générateur, on parle de « surtension ».
aux bornes du générateur, on parle de « surtension ».
D. Quadripôles et filtrage
1. Fonction de transfert en sortie ouverte.
Un quadripôle formé de dipôles linéaires, R, L ou C, reçoit une tension
![]()
et on cherche à déterminer les caractéristiques de la tension
![]()
en sortie du quadripôle.
On définit la fonction de transfert
![]()
On exprime son module et son argument
![]()
* Le module ![]() est le coefficient multiplicatif de l’amplitude :
est le coefficient multiplicatif de l’amplitude :
![]()
* L’argument est le déphasage
![]()
Exemple.
La fonction de transfert d’un quadripôle vaut
![]()
a. Pourquoi le qualifie-t-on de « passe-tout » ?
b. Comment transforme-t-il les signaux de basse fréquence ?
c. Comment transforme-t-il les signaux de haute fréquence ?
Correction :
a. Le module vaut ![]() , quelle que soit la valeur de
, quelle que soit la valeur de ![]() , donc l’amplitude de sortie
, donc l’amplitude de sortie ![]() est toujours égale à celle d’entrée
est toujours égale à celle d’entrée ![]() : c’est un passe-tout.
: c’est un passe-tout.
b. À basse fréquence ![]() et
et ![]()
c. À haute fréquence ![]() et
et ![]()
2. Calcul d’une fonction de transfert.
On se ramène la plupart du temps à la loi du diviseur de tension.
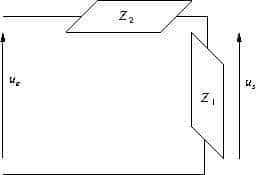
On a alors
![]()
Exemple.
La tension d’entrée est appliquée à un circuit RC série, la tension de sortie est prise aux bornes du condensateur.
Quelle est la fonction de transfert du quadripôle ?
Correction :
Par diviseur de tension
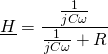
soit ![]()
3. Tracer un diagramme de Bode asymptotique.
On exprime ![]() comme une fraction rationnelle en
comme une fraction rationnelle en ![]()
* L’équivalent à basse fréquence ![]() est le rapport des termes de plus bas degré.
est le rapport des termes de plus bas degré.
On calcule le module ![]() , le gain
, le gain ![]() et l’argument
et l’argument ![]()
* L’équivalent à haute fréquence ![]() est le rapport des termes de plus haut degré.
est le rapport des termes de plus haut degré.
On calcule le module ![]() , le gain
, le gain ![]() et l’argument
et l’argument ![]()
* L’intersection des asymptotes est obtenu quand ![]()
On en déduit la valeur ![]() correspondante.
correspondante.
On calcule ![]() ,
, ![]() et
et ![]()
* On trace le diagramme sur un diagramme semi-logarithmique, en mettant en évidence les asymptotes et leurs pentes typiques, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ou
ou ![]()
Exemple.
Dans le quadripôle du paragraphe précédent, on pose ![]()
Sa fonction de transfert vaut donc
![]()
Dresser le diagramme de Bode en gain.
Correction :
* À basse fréquence![]() donc
donc ![]() et
et ![]()
* À haute fréquence ![]()
donc ![]() et
et ![]()
* Les asymptotes se coupent pour ![]()
![]()
donc ![]() et
et ![]()
On en déduit le diagramme.
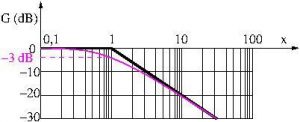
4. Qualifier un quadripôle.
Le diagramme de Bode en gain fait apparaître trois domaines :
* les basses, les moyennes, les hautes fréquences
et trois comportements
* passe (![]() ), coupe (
), coupe (![]() ) et ampli (
) et ampli (![]() )
)
On construit le qualificatif du quadripôle avec un préfixe (passe-, coupe-, ampli-) et un suffixe (bas, bande, haut).
Il est souvent demandé de vérifier ce qualificatif grâce aux schémas équivalents du montage à basse et haute fréquence
* à BF, le condensateur se comporte comme un interrupteur ouvert, la bobine comme un fil
* à HF, le condensateur se comporte comme un fil, la bobine comme un interrupteur ouvert.
Exemple.
Qualifier le filtre du paragraphe précédent, retrouver ce résultat par les schémas équivalents à basse et haute fréquence.
Correction :
Le filtre coupe les haute fréquences et laisse passer les basses : c’est un passe-bas (ou un coupe-haut).
Les circuits équivalents ci-après montrent que
* à BF, ![]() : ça passe
: ça passe
* à HF, ![]() est la tension aux bornes d’un fil donc
est la tension aux bornes d’un fil donc ![]() : ça coupe.
: ça coupe.
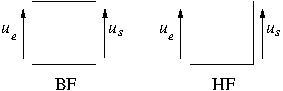
Profitez des cours en ligne de physique de maths sup pour améliorer vos notes et faire la différence en prépa. Si les cours de début d’année sont déjà parfaitement acquis, entamez les prochains chapitres au programme :
- Resume de cours sur la mécanique du point
- Cours en ligne sur les méthodes énergétiques
- Cours gratuit : la loi du moment cinétique maths sup
- Cours en maths sup sur les particules chargées
- Cours sur les forces centrales maths sup
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut


